3D-Animationen
Rotierende 3D Formen
Lösung Aufgabe 7, Kapitel 14 im Lehrbuch
Beginnen wir mit relativ einfachen räumlichen Elementen: Kugel, Zylinder, Säule und Pyramide. Damit man ihre Drehung im Raum beobachten kann, bekommen sie noch Farbe auf ihre Oberfläche. Im folgenden Bild bekommt man eine Ahnung, was sich hier alles drehen soll:
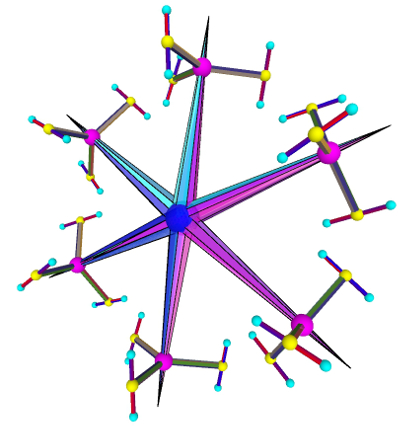
In der Animation unten sieht man einen große sich drehende Stern, der aus sechs sich drehenden transparenten
Pyramiden besteht. Dies ist die Version für Smartphones. (Die "Computerversion" ist für das Smartphone mitunter
zu rechenaufwändig!)
In der komplexeren Version
erkennt man außerdem magentafarbene Kugeln, die drei Säulen halten. Die Prismen rotieren ebenfalls und tragen
am Ende gelbe Kugeln. Zugegeben, das Ganze sieht ziemlich kompliziert aus.
Die gute Nachricht ist, dass der Programmcode, was die Rotationen angeht, recht einfach ist.
Hier gehts erweiterten Animation
Betrachten wir den Abschnitt des Programms, bei dem eine große Pyramide des Sterns, eine magentafarbene Kugel
und ein Prisma gezeichnet ist. Dann fehlen eine gelbe Kugel, zwei Zylinder mit jeweils einer cyanfarbenen Kugel.
Außerdem sind in diesem Zustand noch zwei Rotationen durchzuführen: die um das Prisma als Achse und die Drehung
der Zylinder selbst. Und so sieht der Code dazu aus:
translate(0, 125, 0);
rotateY(k+gamma);
fill(255,255,0);noStroke();
sphere(11);
fill(80, 130, 250);
rotateZ(k+epsilon);
saeuleZeichnen(60,4, 55 ); // Die in den gelben Kugeln steckende Säulen
translate(0,0,55);
fill(0,255,255);
noStroke();
sphere(8);
popMatrix();
Die Pyramiden und Säulen sind "Shapes". Hier finden Sie ein Tutorial zum Thema.
Sketch rotationen.
Menu