Menu

3D mit Processing

Analytische Flächen: Überblick

Das vorliegende Kapitel behandelt die Darstellung analytischer Flächen im 3-dimensionalen Raum. Ein Beispiel sehen Sie im Bild oben. Die Mathematik dahinter ist unvermeidbar, wenn man dieses große Gebiet bezüglich der Darstellbarkeit der Flächen bearbeiten will. Dennoch beschränken wir uns diesbezüglich auf ein Minimum und nehmen dafür in Kauf, dass nicht alle mathematischen Formulierungen der reinen Lehre entsprechen. Auf ganz natürliche Weise wird sich uns eine Einordnung der verschiedenen Flächen aufdrängen, ohne dass wir uns dabei in endlosen Definitionen verlieren müssen.
Die erste Frage: Was sind analytische Flächen im 3-dimensionalen Raum? Fürs Erste genügt es, eine grobe Vorstellung davon zu bekommen, indem wir ganz einfach sagen: "So etwas, wie im Bild oben". (Aber keine Sorge - es wird nach und nach etwas genauer formuliert werden ;-))

Explizite Flächen

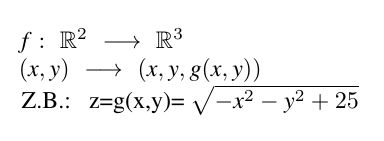
Explizite Flächen werden durch Abbildungen f, wie im Bild links dargestellt, erzeut. Man kann den Vorgang mit den von der Schule bekannten Schaubildern in der Eben vergleichen. Dort wurde einem Wert x ein Wert y zugeordnet. (x,y) ist dann ein Punkt der Ebene, der, bei kartesischen Koordinaten, senkrecht über der Stelle x liegt. In unserem Fall liegt der neue Punkt (x,y,z) senkrecht über dem Punkte (x,y). Allerdings kann, da g ebenfalls eine Funktion und somit eindeutig ist , einem Punkt (x,y) der Ebene nur genau ein Punkt (x,y,z) des Raumes zugeordnet werden. Die ganz oben gezeigte Fläche ist also mit Sicherheit keine explizite Fläche.
Das Beispiel unter der Definition von f stellt eine Halbkugel mit Radius R = 5 dar:
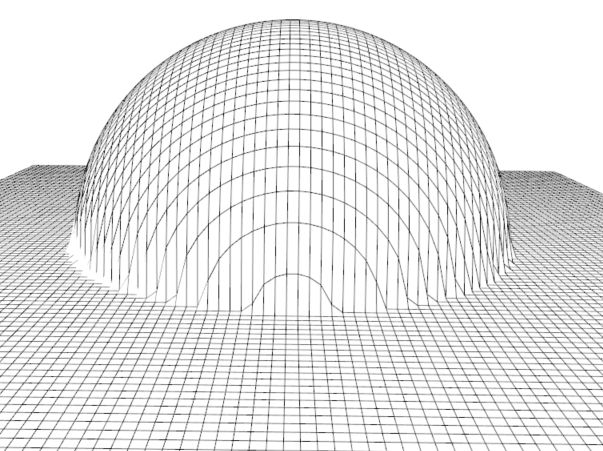
Die ebenen Vierecke im Bild "pflastern" die Halbkugel. Das Bild zeigt daher nicht die Fläche, sondern ein Netz (Mesh), das die Fläche annähert. Je kleine die Vierecke, desto genauer wird die explizite Fläche angenähert.

Parametrische Flächen

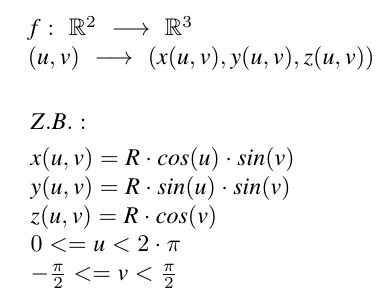
Parametrische Flächen werden durch Abbildungen f, wie im Bild links dargestellt, erzeut. Obwohl f eine durch drei Funktionen erzeugte Funktion ist, sind nun geschlossene Flächen möglich. Der Definitionsbereich ist hier ganz wesentlich: Würde man den Bereich für u oder v verkleinern, könnte keine vollständige Kugeloberfläche entstehen. Andererseits, würde man die Bereiche vergrößern, dann gäbe es Bereiche der Fläche, die mehrfach erzeugt werden würden.
Die Parameter u und v sind im vorliegenden Beispiel (Kugeloberfläche mit Radius R) Polarkoordinaten. Der Definitionsbereich ist daher ein bei 2 π offenes Rechteck mit den Eckpunkten (0;- π/2), (2 π ; - π/2),(0; π/2) und (2 π ; π/2).

Implizite Flächen

Implizite Flächen sind Nullstellen-Mengen. Die erste Gleichung unten hat als Lösung eine Sphäre (Kugeloberfläche). Wenn man die explizite Form der halben Sphäre ganz oben auf beiden Seiten quadriert und alle Variablen auf eine Seite bringt, dann bekommt man ebenfalls die Gleichung wie unten. Durch das Quadrieren sind nun auch die negativen z-Werte dabei und es verwundert nicht, dass die Nullstellen-Menge genau die Kugeloberfläche mit Radius 5 ist. Dennoch sind beide Formen voneinander zu unterscheiden. Bei den expliziten und bei den parametrischen Flächen sind die Punkte Funktionswerte. Bei impliziten Flächen handelt es sich um eine durch eine Gleichung definierte Menge.

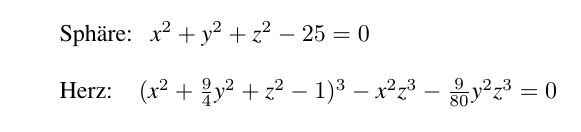
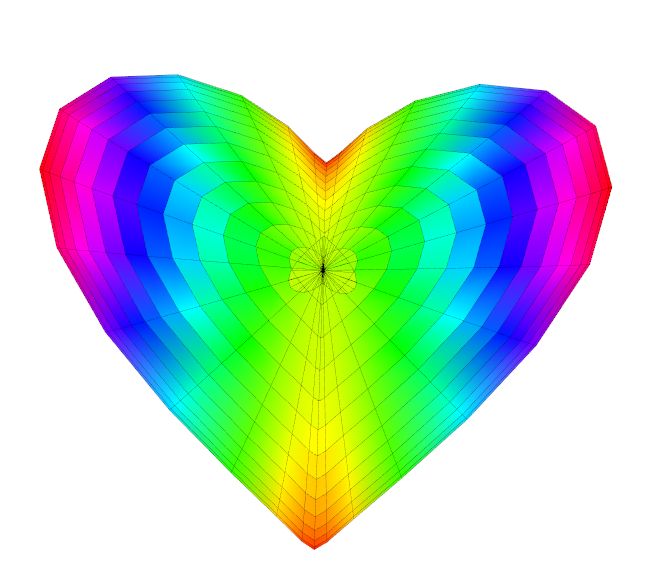
Das folgende Bild wurde durch die "Herz-Gleichung" oben erzeugt. Man kann schon hier ahnen, dass eine "Umrechnung" der impliziten in z.B. die explizite Form kaum zu schaffen ist. Wie man dennoch derartige Flächen zeichnen kann, lernen Sie im Kapitel "Implizite Flächen". Zur Abwechslung haben wir hier die kleinen Rechtecke so gefärbt, dass der Abstand eines vorher festgelegten Rechteckpunktes vom Nullpunkt in der Mitte die Farbe bestimmt.

Grid und Mesh

Wie zeichnet man mit Processing derartige Flächen? In den folgenden Kapiteln werden wir ausführlich darauf eingehen. Aber auch schon hier sollen Sie einen ersten Überblick bekommen. Der Einfachheit halber, betrachten wir zunächst nur die ersten beiden Flächen: explizte und parametrische.
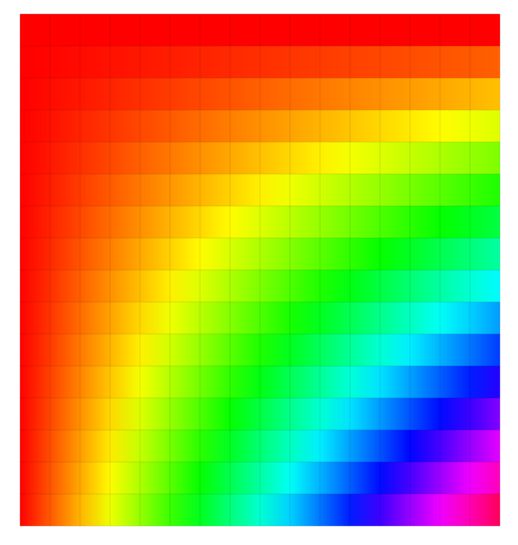
Wie Sie wissen, stellt und Processing einen mächtigen 3D-Renderer namens P3D zur Verfügung. Man benötigt daher für den Definitionsbereich der Funktionen ein 2-dimensionales Gitter(Grid), der Definitionsmenge, das um so engmaschiger sein muss, je genauer das Bild der Fläche werden soll. Das Bild unten zeigt ein solches Grid. Falls Sie vergessen haben sollten, wie man es erstellt, hier eine kurze Hilfe zur Erinnerung: Man verwendet zeilenweise die Funktion Shape(QUAD_STRIP), bei dem immer zwei Punkte an die letzten beiden Punkte angehängt werden und so ein neues Viereck bilden. Die 16 ix-Werte laufen von links nach rechts, die ebenfalls 16 iy-Werte von oben nach unten. Farbe bekommen wir durch fill(ix*iy,255,255), wobei wir hier das HSB-Farbsystem verwenden. Von daher ist klar, dass die erste Zeile und die erste Spalte rot sein muss, denn die Zählung beginnt bei Null und der Hue-Wert Null entspricht rot.

Ein Mesh bekommt man, wenn man die Eckpunkte des Grid in die entsprechende Funktionen einsetzt. Man beachte aber, dass konstruktionsbedingt nur Streifen von Grids eingesetzt werden. Damit hat unser Mesh den Schönheitsfehler, aus lauter nicht zusammenhängende Streifen zu bestehen. Für die Darstellung der Fläche spielt das keine Rolle. Wenn wir aber später solche Flächen im 3D-Drucker erzeugen wollen, müssen wir uns etwas einfallen lassen.
Sie sehen im Bild unten links, dass statt Vierecken auch Dreiecke verwendet werden können. Für die Färbung gibt es unzählige Möglichkeiten: Abstand vom Ursprung, Höhe, einfarbig, ...
Im folgenden Bild ist schon fast alles enthalten, was man wissen muss:

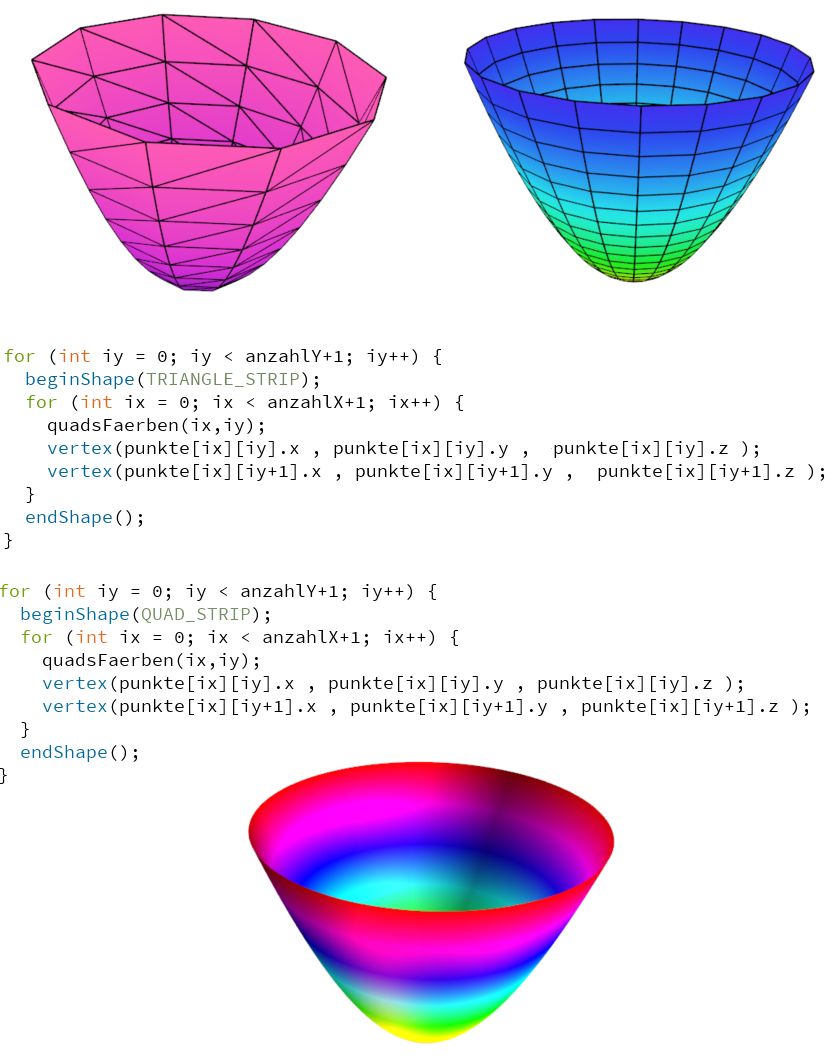
In allen drei Fällen verwendet man die gleiche explizite Funktion. Im letzten Bild allerdings ist das Mesh sehr engmaschig gewesen und außerdem hat man auf das Zeichnen der Begrenzungen der Drei/Vierecke verzichtet.

Menu