Chaos Game: Übersicht
Die Attraktore, die wir hier erzeugen, sind größtenteils Fraktale. Die Methode aber, wie wir diese Attraktore
erzeugen, unterscheiden sich erheblich von den bisherigen Methoden. Die Punkte werden zufällig über den Attraktor
verteilt. Bisher wurde im Gegensatz dazu bei jedem einzelnen Punkt geprüft, ob er zum Fraktal gehört oder nicht.
Wer zum ersten Mal mit dieser Methode arbeitet, dem kommt das Ganze wie Hexerei vor. Daher werden wir uns in einem
Folgekapitel die "Hexerei" etwas genauer anschauen.
Verwendet wurde die Methode ursprünglich zum Erzeugen von Fraktalen, indem man die Eckpunkte eines Polygons
und eines beliebigen Startpunktes im Polygon verwendet. Am besten, Sie schauen sich das bei einem Dreieck
mal selbst an.
Die Eckpunkte des Dreiecks sind farblich markiert. In der Mitte befindet sich der (schwarze) Startpunkt. Ein weiterer
Punkt der Folge ist bereits eingetragen. Er liegt auf der Hälfte der Strecke zu einem Eckpunkt. Seine Farbe wird
durch den Eckpunkt, in dessen Richtung er sich befindet, festgelegt. Jetzt sind Sie dran. Klicken Sie auf "e",
um einen Folgepunkt hinzuzufügen. Er wird dadurch erzeugt, dass man zufällig einen Eckpunkt auswählt und die Mitte
zwischen dem letzten Punkt und eben dieser Ecke bestimmt. Seine Farbe richtet sich nach der ausgewählten Ecke.
Bei jedem Druck auf "e" wird auf diese Art ein weiterer Punkt hinzugefügt.
Beschleunigen kann man den Vorgang, indem man mit "h" jedes Mal 100 Punkte hinzufügt. Wem das noch zu langsam ist
wählt "t", und fügt jeweils 50000 Punkte hinzu. (Die Tasten k und g werden erst später benötigt.)
Mit etwas Geduld sehen Sie nach einiger Zeit das folgende Bild:
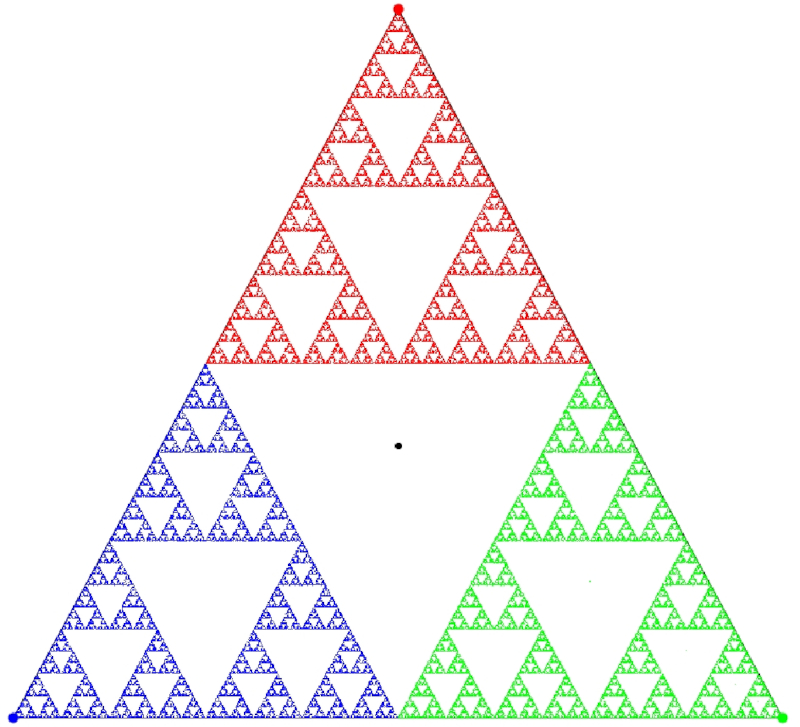
Und das ist nichts anderes, als das Sierpinski Dreick, dass wir im Lehrbuch auf völlig andere Weise erzeugt haben.
Inzwischen verwendet man eine Verallgemeinerung der Chaos-Game-Methode auch für die Fixpunkt-Bestimmung bei
Attraktoren und vor allem aber bei IFS (Iterated Function System) und damit auch zur Erzeugung von "Fractal Flames".
Mit den letzten beiden Anwendungen werden wir uns später noch genauer beschäftigen.
Man muss beim Chaos Game nicht unbedingt die Mitte zwischen Punkt und Eckpunkt wählen. Verwenden wir allgemeiner
den Faktor k, dann sieht der Algorithmus folgendemaßen aus:
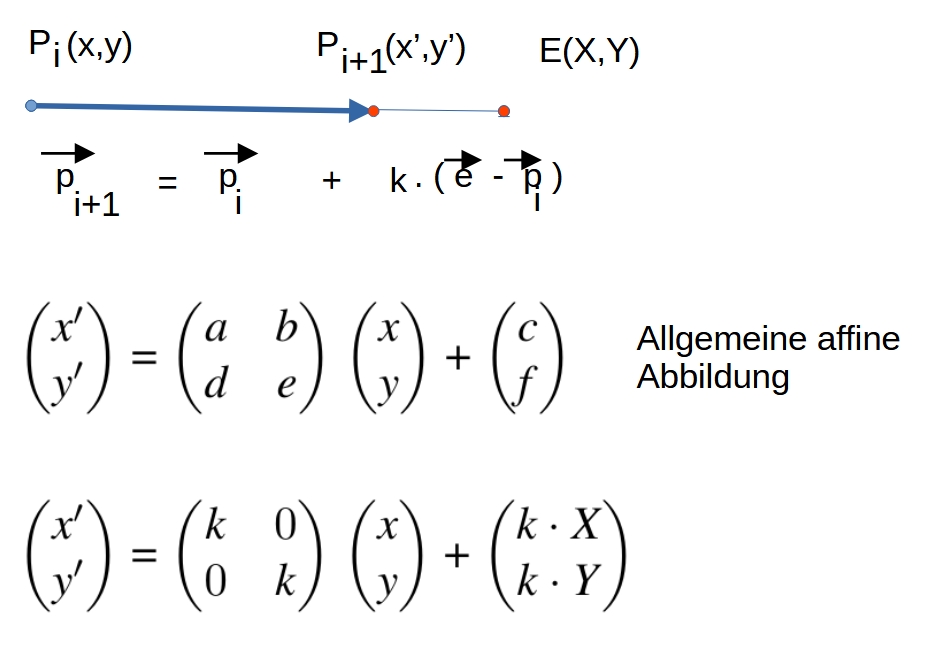
E ist hier ein Eckpunkt des n-Ecks und Pi der abzubildende Punkt.
Beachten Sie, dass k auch größer als 1 sein kann. In diesem Fall liegt der Bildpunkt außerhalb des n-Ecks.
Wenn Sie nicht mehr wissen, was eine affine Abbildung ist, dann können Sie sich
hier informieren.
Es handelt sich in unserem Fall offensichtlich um einen Spezialfall einer affinen Abbildung.
In Processing sieht das im allgemeinen Fall so aus:
x = a*X + b*Y + c;
y = d*X + e*Y + f;
X = x;
Y = y;
}
Bisher galt k = 0.5. Was passiert, wenn man k größer oder kleiner als 0.5 wählt? Das können Sie in der Anwendung oben ausprobieren. Die Taste "k" verkleinert bei jedem Druck den Wert von k um 0,02, die Taste "g" nacht genau das Gegenteil: Bei jedem Druck wird k um 0,02 vergrößert. Im Bild unten ist links k = 0,44 und rechts k = 0,54.
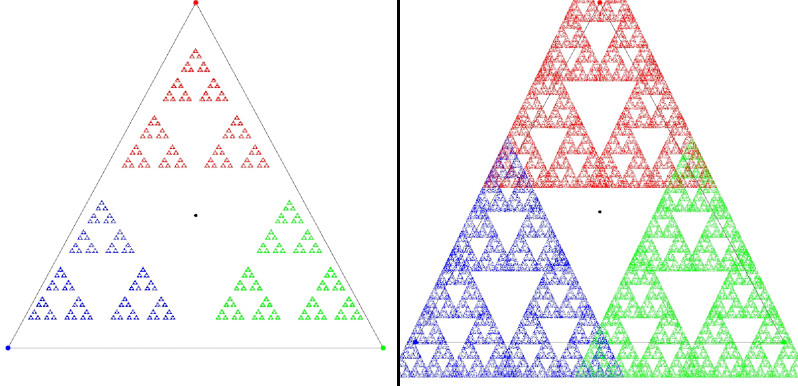
Und wie sieht die Sache mit vier Ecken, also bei einem Quadrat aus? Links ist k = 0.5 wie oben und rechts gilt k = 0.6.
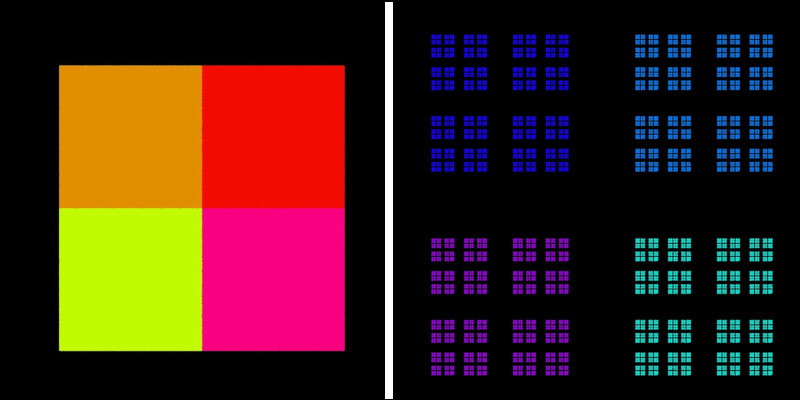
Im ersten Fall gibt es keinen Attraktor. Die Punkte sind chaotisch über ihr Quadrat-Viertel verteilt. Der zweite Fall erinnert stark an den sogenannten Cantor Dust im Kapitel "Maps".
Sketch ChaosGameDemo
Menu