Chaos Game: Iterated Function System (IFS) 2
In den nächsten Beispielen behandeln wir, wie am Ende des letzten Kapitels, fast ausschließlich Dichte-Bilder.
Leider ist es nicht einfach zu einem Bild ein passendes erzeugendes IFS zu finden. Konkretes Beispiel: Wie kann
man mit IFSs einen Baum zeichnen? Schauen wir uns einige Beispiele an:
Baum IFS
Man benötigt sieben Parameter: a, b, c, d, e, f und wkt für jede affine Abbildung. wkt ist hierbei die Wahrscheinlichkeit, mit der die zugehörige affine Abbildung gewählt wird. (Auf die Farbe kann man verzichten, wenn man ein Dichte-Bild erzeugen will.) Wir verwenden hierzu eine Tabelle, deren Struktur für alle folgenden Beispiele übernommen werden kann:
| a | b | c | d | e | f | wkt |
| a[1]=0.05 | b[1]=0 | c[1]=0 | d[1]=0.6 | e[1]=0 | f[1]=0 | wkt[1]=0.28 |
| a[2]=0.05 | b[2]=0 | c[2]=0 | d[2]=−0.5 | e[2]=0 | f[2]=1 | wkt[2]=0.28 |
| a[3]=0.46 | b[3]=−0.32 | c[3]=0.39 | d[3]=0.38 | e[3]=0 | f[3]=0.6 | wkt[3]=0.2 |
| a[4]=0.47 | b[4]=−0.15 | c[4]=0.17 | d[4]=0.42 | e[4]=0 | f[4]=1.1 | wkt[4]=0.02 |
| a[5]=0.43 | b[5]=0.28 | c[5]=−0.26 | d[5]=0.45 | e[5]=0 | f[5]=1 | wkt[5]=0.2 |
| a[6]=0.42 | b[6]=0.26 | c[6]=−0.35 | d[6]=0.31 | e[6]=0 | f[6]=0.7 | wkt[6]=0.02 |
Danach kann man den fogenden Code für alle anderen Beispiele verwenden. Nur die Anzahl der Aufrufe der Methode addTransform und der Wert der Parameter kann variieren.
ifs2 = new IFS("Baum");
ifs2.addTransform(a[1], b[1], c[1], d[1], e[1], f[1], wkt[1], 1);
ifs2.addTransform(a[2], b[2], c[2], d[2], e[2], f[2], wkt[2], 2);
ifs2.addTransform(a[3], b[3], c[3], d[3], e[3], f[3], wkt[3], 3);
ifs2.addTransform(a[4], b[4], c[4], d[4], e[4], f[4], wkt[4], 4);
ifs2.addTransform(a[5], b[5], c[5], d[5], e[5], f[5], wkt[5], 5);
ifs2.addTransform(a[6], b[6], c[6], d[6], e[6], f[6], wkt[6], 6);
ifs2.addTransform(a[1], b[1], c[1], d[1], e[1], f[1], wkt[1], 1);
ifs2.addTransform(a[2], b[2], c[2], d[2], e[2], f[2], wkt[2], 2);
ifs2.addTransform(a[3], b[3], c[3], d[3], e[3], f[3], wkt[3], 3);
ifs2.addTransform(a[4], b[4], c[4], d[4], e[4], f[4], wkt[4], 4);
ifs2.addTransform(a[5], b[5], c[5], d[5], e[5], f[5], wkt[5], 5);
ifs2.addTransform(a[6], b[6], c[6], d[6], e[6], f[6], wkt[6], 6);
Mit diesen Werten und 100 Millionen Iterationsschritten bekommt man bei geeigneter Farbtafel dieses Bild:
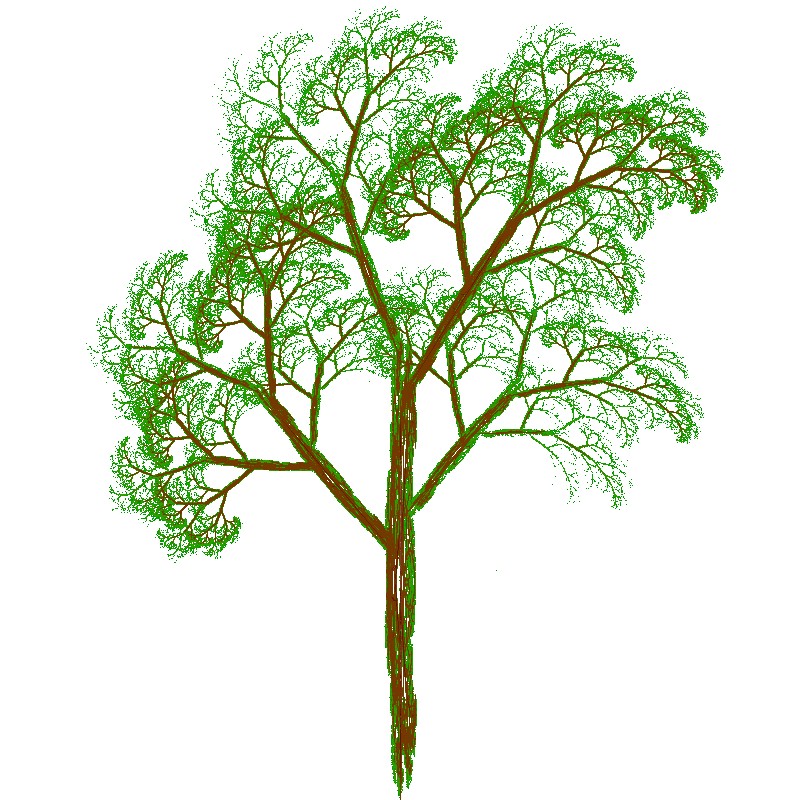
Wenn man alle Parameter zufällig wählt, erhält man höchst selten ein attrakives Bild. Besser ist es, wenn man bei den aktuellen Werten nur wenige dem Zufall überlässt. So zum Beispiel alle b und c Parameter.

In diesem Fall kann man, trotz der zufälligen Wahl aller b- und c-Parameter, noch Elemente des vorherigen Bildes erkennen.
Blatt IFS
Zur Erzeugung eines "Blatt-IFS" benötigt man nur vier affine Abbildungen. Mit diesen Werten sollte es klappen:
| a | b | c | d | e | f | wkt |
| a[1]=0.14 | b[1]= 0.01 | c[1]=0 | d[1]=0.51 | e[1]=−0.08 | f[1]=−1.31 | wkt[1]=0.25 |
| a[2]=0.43 | b[2]=0.52 | c[2]=−0.45 | d[2]=0.5 | e[2]=1.49 | f[2]=−0.75 | wkt[2]=0.25 |
| a[3]=0.45 | b[3]=−0.49 | c[3]=0.47 | d[3]=0.47 | e[3]=−1.62 | f[3]=−0.74 | wkt[3]=0.25 |
| a[4]=0.49 | b[4]=0 | c[4]=0 | d[4]=0.51 | e[4]=0.02 | f[4]=1.62 | wkt[4]=0.25 |
Da die Anzahl der Treffer pro Pixel stark variiert, sollte man, wie beim vorherigen Beispiel auch, den Logarithmus der Trefferanzahl verwenden. Hier ist der Farbverlauf sehr einfach gehalten. Es werden im Wesentlichen Grün- und Brauntöne verwendet.

Auch hier bringt eine sparsam genutzte Zufallswahl einiger Parameter, verblüffende Bilder hervor:
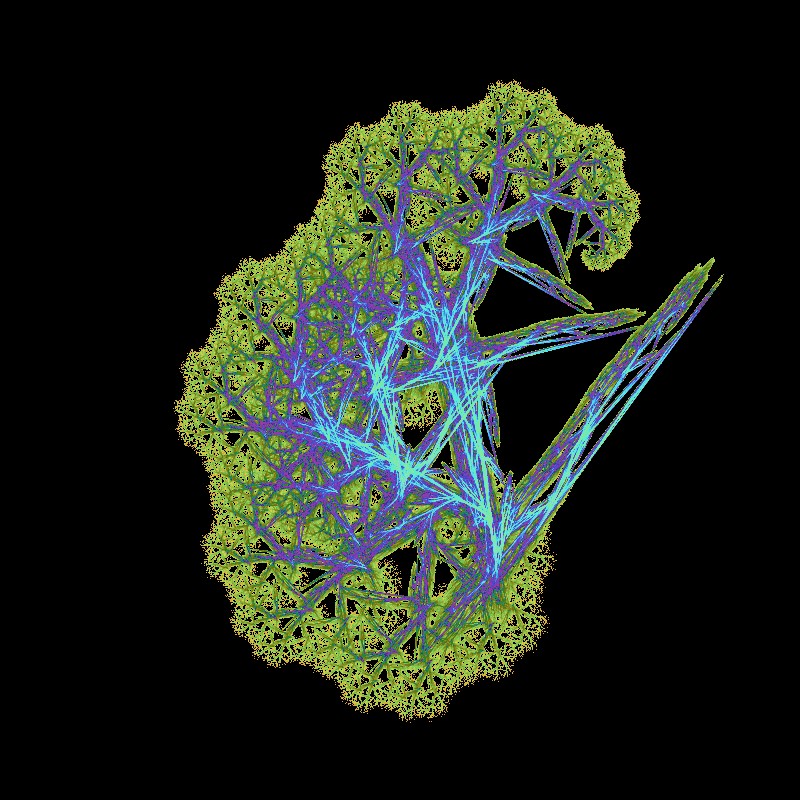
Gras IFS
Ein grasähnliches Bild erreicht man mit diesen Parametern:
| a | b | c | d | e | f | wkt |
| a[1]=0 | b[1]=0.2439 | c[1]=0 | d[1]=0 | e[1]=0 | f[1]=0 | wkt[1]=0.25 |
| a[2]=0.7248 | b[2]=0.0337 | c[2]=−0.0253 | d[2]=0.7426 | e[2]=0.206 | f[2]=0.2538 | wkt[2]=0.25 |
| a[3]=0.1583 | b[3]=−0.1297 | c[3]=0.355 | d[3]=0.3676 | e[3]=0.1383 | f[3]=0.175 | wkt[3]=0.25 |
| a[4]=0.3386 | b[4]=0.3694 | c[4]=0.2227 | d[4]=−0.0756 | e[4]=0.0679 | f[4]=0.0826 | wkt[4]=0.25 |
Viele Millionen Iterationschritte (wenige Sekunden für den PC!) bringen dieses Bild zum Vorschein:

Ändert man noch weniger Parameter als im letzten Beispiel, dann bekommt man ein anderes distelähnliches Gebilde.

Spiralen IFS
Wer die Parameter in bestimmten Grenzen zufällig wählt, bekommt als Ergebnis meist ein mehr oder weniger großes Chaos-Bild. Mitunter aber erscheint plötzlich eine etwas interessantere Form. Ein Bild mit vielen Spiralen erscheint, wenn man diese Parameter wählt:
| a | b | c | d | e | f | wkt |
| a[1]=0.7868 | b[1]=−0.4237 | c[1]=0.2431 | d[1]=0.8602 | e[1]=1.7658 | f[1]=1.4103 | wkt[1]=0.9 |
| a[2]=− 0.1220 | b[2]=0.0337 | c[2]=0.1508 | d[2]=0.5310 | e[2]=−6.7195 | f[2]=0.3822 | wkt[2]=0.05 |
| a[3]=0.1827 | b[3]=−0.1372 | c[3]=0.0901 | d[3]=0.1791 | e[3]=6.0877 | f[3]=1.5693 | wkt[3]=0.05 |
Vielleicht ist Ihnen aufgefallen, dass e[2] und e[3] betragsmäßig deutlich größer als 1 sind. Und oberhalb von 1 besteht grundsätzlich die Gefahr, dass die Folgenelemente divergieren. Erst recht natürlich bei Beträgen größer 6. Damit überhaupt eine Chance auf einen Attraktor besteht, darf die Wahrscheinlichkeit für diese beiden affinen Abbildungen nur mit einer sehr kleinen Wahrscheinlichkeit ausgewählt werden. Eine Garantie für Beschränktheit hat man dennoch nicht. So wird es immer wieder vorkommen, dass nur einige wenige Punkte zu sehen sein werden.
Mit den obigen Einstellungen aber funktioniert die Sache aber. Das Ergebnis so aus:

Für das Bild unten wurden nur einige b- und c-Parameter leicht verändert. Und schon sieht das Ergebnis aus, wie ein Lebewesen aus der Tiefsee. Es lohnt sich offensichtlich, bei interessanten Bildergebnissen, nur kleine Parameteränderungen vorzunehmen. Es ist fast sicher, dass das Ergebnis noch niemand zuvor gesehen hat ;-)

Drachen IFS
Als letztes Beispiel behandeln wir diese urtümliche Fabelwesen:
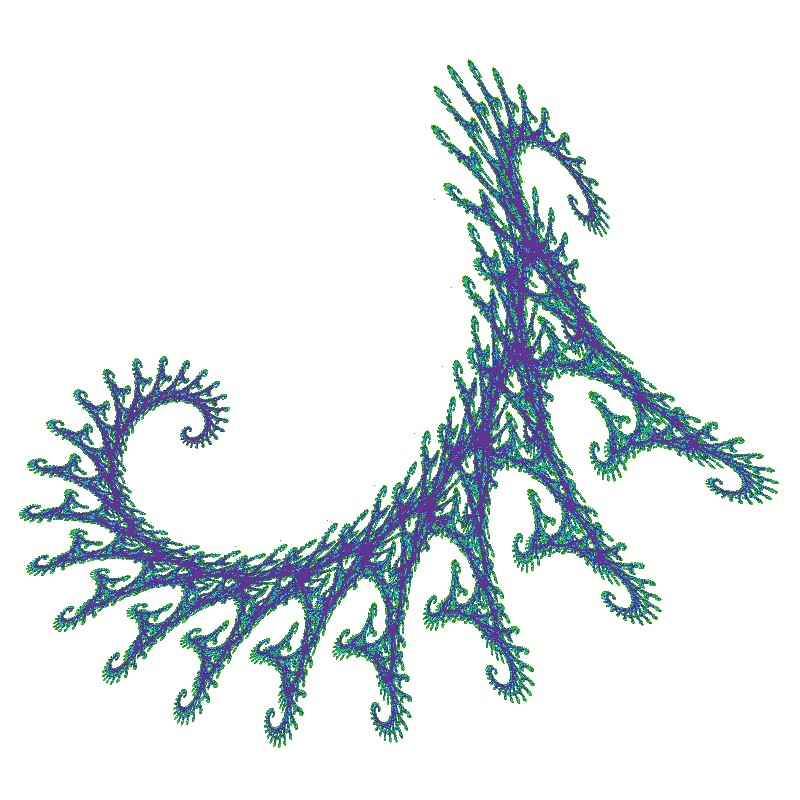
Mit einiger Phantasie kann man einen Drachen erkennen. Hier sind die Parameter:
| a | b | c | d | e | f | wkt |
| a[1]=0.8240 | b[1]=0.2814 | c[1]=−0.2123 | d[1]=−0.8642 | e[1]=−1.8823 | f[1]=−0.1106 | wkt[1]=0.8 |
| a[2]=0.0883 | b[2]=0.5210 | c[2]=−0.4639 | d[2]=−0.3778 | e[2]=0.7845 | f[2]=8.0958 | wkt[2]=0.2 |
Kleine Änderungen in den Parametern b und c bringen dieses Bild zum Vorschein:
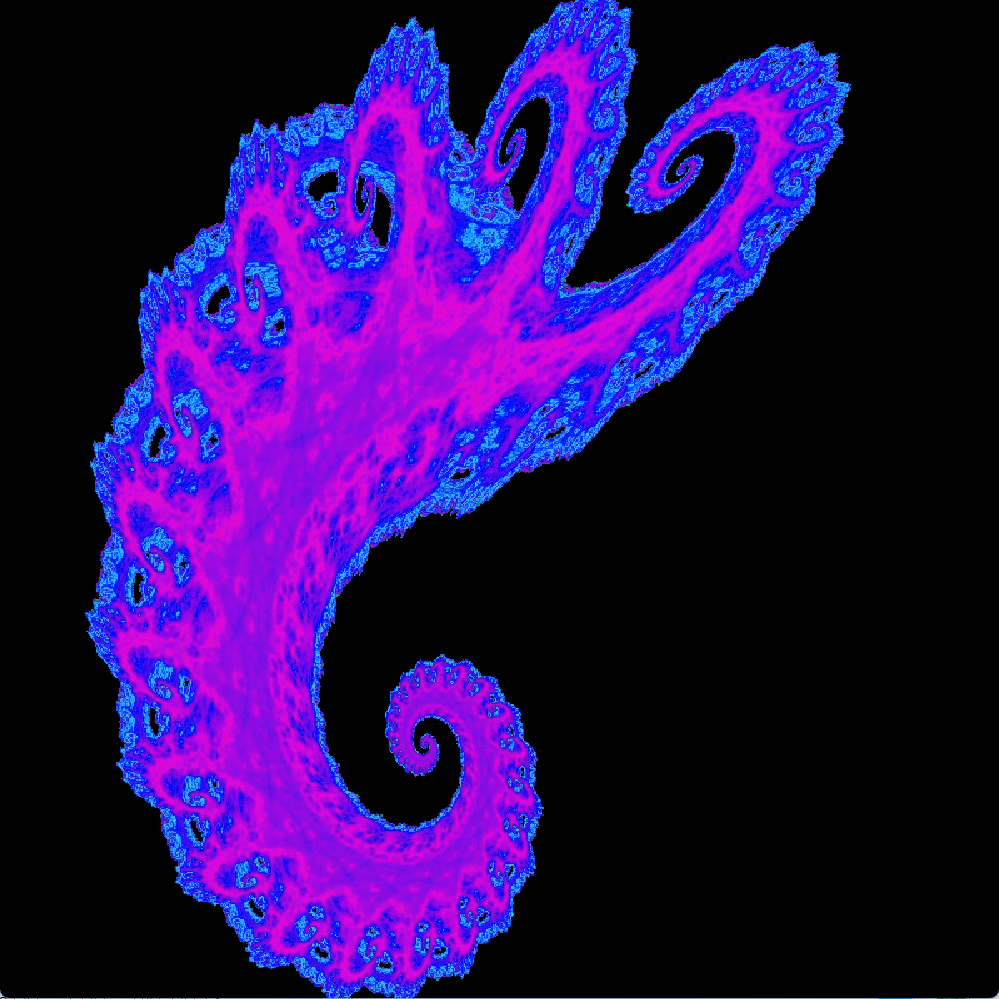
Sketch IFSBaumDichte Sketch IFSBlattDichte
Sketch IFSGrasDichte Sketch IFSSpiralenDichte
Sketch IFSDracheDichte
Menu