Menu

Bildbearbeitung

Faltung (Convolution)

Eine Faltung ist lineare Abbildung. Eine Matrix wird mit Hilfe eines "Faltungskernels" in eine andere Matrix abgebildet. Um sie auf Bilder anzuwenden, müssen diese zunächst in Matrizen verwandelt werden. Beachten Sie dabei: Wenn man die Größe des Programmfensters durch z.B. size(800,600) angibt, dann verwendet man häufig für den weiteren Programmcode w = width ; h = height; . Auch wenn man die Größe eines Bildes angeben will, wird als erste Zahl immer die Breite des Bildes und danach die Höhe angeben. Selbst dann, wenn Bild und Programmfester gleich groß sein sollten, tut man gut daran, neue Buchstaben bei den Bilddimensionen zu verwenden. Zum Beispiel W =bildOriginal.width; H = bildOriginal.height; . Weshalb auch bei gleichen Werten? Es liegt daran, dass die Matrizen die Reihenfolge von Breite und Höhe andersherum verwenden. Die Matrix zu obigem Bild wäre dann bearbeitetMatrix = new int[H][W]; Falls Sie das entsprechende Kapitel im Lehrbuch nicht gelesen haben sollten, hier eine Realisierung in Processing:

Versuchen Sie nun, den Programmcode für die Umwandlung einer Matrix in ein Bild zu schreiben. Wenn Sie Hilfe brauchen, schauen Sie sich den dazu passenden Sketch an. Dort wird auch gezeigt, wie man den Dialog "Datei öffnen" umsetzt. Außerdem ist mit einer Programmzeile dafür gesorgt, dass die schwarzen Pixel eines Bildes gezählt werden. Dies wird uns später nützlich sein.
Das folgende Bild zeigt an einem Beispiel, wie Faltungen durchgeführt werden:


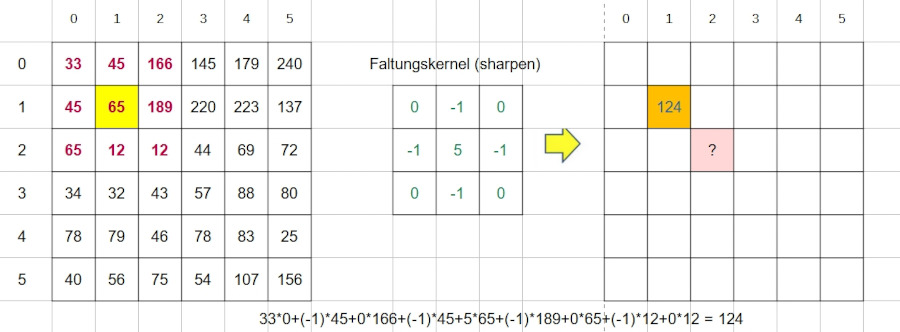
Der Faltungskernel wird zunächst mit dem violett dargestellten Teil der Ausgangsmatrix multipliziert (Zeile mal Spalte). Die Rechnung ist unter dem Bild dargestellt. Aus 65 wird somit 34. Was wird dann aus der 12 unter 189? (Lösung am Seitenende)
Was genau tut der Faltungskernel im obigen Fall? Vier Nachbarpixel (-1) bewirken, dass der abzubildende Wert (65) sich von eben diesen Nachbarn stärker unterscheidet. Das Bild gewinnt daher an Schärfe.
Die Ränder der Matrix allerdings kann man mit dieser Methode leider nicht abbilden. Es gibt verschiedene Methoden, dieses Manko zu beheben. Die einfachst ist, die zugehörigen Randpixel wegzuschneiden. Bei einem Pixel von vielleicht 2000 Pixeln Bildbreite, ist dies akzeptabel.
Will man bei der Durchführung der Faltung noch weitere Umgebungswerte des abzubildenden Wertes einbeziehen, dann verwendet man eine 5x5, 7x7 oder 9x9 Matrix als Faltungskernel. Dadurch lässt sich letztendlich das Bild sehr viel feiner bearbeiten.

Kanten finden mit Sobel

Hierfür benötigt man zwei Kernel. Einen für die x- und einen für die y-Richtung. Das Ergebnis der Faltung ist eine näherungsweise Ableitung in x- und y-Richtung. Man stelle sich einfach vor, dass als Funktionswerte die Grauwerte der jeweiligen Pixel verwendet werden. Da dies nur diskrete Werte sind, ist die Ableitung für jedes Pixel dx bzw. dy. Dies sind die beiden Sobel-Kernel:
Schauen wir uns an einem einfachen Bild an, wie die beiden Faltungskernel arbeiten:


Das Bild eines massiven Achtecks ist links zu sehen. Rechts daneben zunächst die Anwendung von gMartrixX auf dieses Bild, also derjenigen Matrix, die eine Näherung der Ableitung in x-Richtung bewirkt. Die Ableitung in eine Richtung ist dann groß, wenn sich der Grauwert stark ändert. Sie ist Null, wenn er gleich bleibt. Weshalb also sind hier die waagerechten Kanten des Achtecks nicht zu sehen? Die Ableitung in diese Richtung bleibt gleich, und somit sind alle dortigen Pixel schwarz.
(Der Einfachheit halber behandeln wir hier nur Graustufenbilder. Falls man Farbe verwenden will, muss man jeden Farbkanal so behandeln, wie wir es mit den Graustufen gemacht haben.)
Das dritte Bild in der obigen Reihe zeigt das Ergebnis, wenn man nur gMartrixY auf das Original anwendet. Das Bild ganz links ist durchaus überzeugend, wenn das Ziel war, die Kanten zu finden. Irgend wie müssen hier beide Faltungskernel angewand worden sein. Wie genau man hier vorgeht, zeigt das folgende Bild:
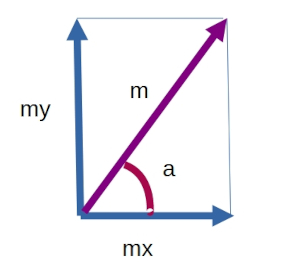
Mit dem Satz des Pythagoras bekommen wir die effektive Ableitung und zusätzlich, mit Hilfe des inversen Tangens, einen Winkel a. Im ersten Augenblick scheint diese Information obsolet. Kurze Überlegung: Wieviele Nachbarn hat ein Pixel, das nicht am Rand liegt? Wenn wir die diagonalen Pixel hinznehmen, sind es acht. Die zugehörigen Winkel sind 0, 45, 90 und 135 Grad. Dazu kommen die jeweils um 180 Grad größeren Winkel 180, 225,... Nun runden wir den Winkel a so, dass er zu einem dieser Winkel wird. Also 30 Grad wird zu 45 Grad, 96 Grad zu 90 Grad usw..
Das besagte Pixel bekommt hierdurch zwei Nachbarn, mit der Eigenschaft, dass sich in dieser Richtung der Grauwert am stärksten ändert. Stellen wir uns vor, dass einer dieser Nachbarn einen höheren Grauwert besitzt, als besagtes Pixel selbst. Wenn wir in diesem Fall genau dieses Pixel schwarz einfärben, dann wird die Kante enger begrenzt und somit präziser.
Schauen Sie sich in folgendem Bild die konkrete Situation für ein bestimmtes Pixel an:


Links ist die Faltung ohne Korrektur zu sehen. Wenn wir die Ecke oben links als (0,0) bezeichnen, dann betrachten wir hier das Pixel (3;2). Unten sind die zugehörigen Winkel eingetragen, hier also 45 Grad. (Die y-Achse zeigt bei Processing nach unten, daher sind 45 Grad hier -45 Grad. ) Beide zugehörigen Nachbarn senkrecht zur Ausbreitungsrichtung haben einen höheren Grauwert als das Pixel selbst. Durch die Korrektur wird das Pixel daher schwarz einfärbt und macht die Kante damit schmaler. Sehen wir uns das Erbnis bei einem vollständigen Bild an:





Oben das Original, danach Anwendung von Sobel ohne Korrektur (mit Invertierung und Schwellenwert). Darunter das entsprechende Ergebnis mit Korrektur. Der Schwellenwert sorgt dafür, dass helles Grau weiß wird. Sehr schön ist dabei zu sehen, dass ohne Korrektur dunklere Bereiche, zum Beispiel für die Wolken, auch nach der Anwendung des Schwellenwertes bleiben. Um zu verstehen, was das bedeutet, sehen wir uns das folgende Bild an, bei dem weder Invertierung noch Schwellenwert angewandt wurde:



Die Korrektur wurde hier durchgeführt. Ohne Korrektur wäre daher der Bereich der hellen Pixel deutlich größer, was dann bei der Invertierung zu weniger präzisen Kanten führt.

Kanten finden mit Scharr

Die Sobel-Methode zur Bestimmung der Ableitungen ist nur eine Näherung. Etwas bessere Ergebnisse bei der Suche nach Kanten bekommt man mit der Scharr-Methode. Dies sind die zugehörigen Faltungs-Kernel:
Hier ein Beispiel, das mit den Scharr-Kernel berechnet wurde. Korrektur, Invertierung und Schwellenwert wurden ebenfalls angewendet:






Lösung der obigen Aufgabe: -228. Wird zu 228, falls die Zahlen Grauwerte zwischen 0 und 255 darstellen.



Sketch bildBearbeitungen.

Menu