Epizykoide
Wenn Sie noch nicht wissen, was Epizykloide sind, dann schauen Sie sich zuvor die ausgezeichnete Seite
von Norbert Treitz an.
Das folgende Bild macht das Vorgehen anschaulich:
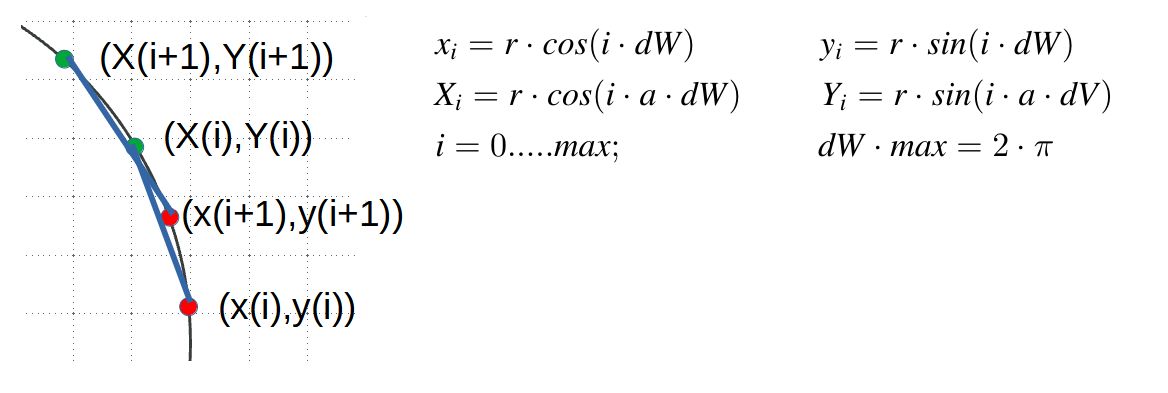
Dabei ist dW der Winkel im Bogenmaß, der einem Schritt entspricht. Wenn dW (in Grad ausgedrückt) zum Beispiel
1 Grad ist, dann muss max 360 sein, damit der ganze Kreis durchlaufen wird. Bei den Epizykloiden ist
der Parameter a für X und Y gleich. Es lohnt sich dennoch, auch verschiedene Parameter für X und Y zu
wählen. Damit beschäftigen wir uns ausführlich im Kapitel Lissajous .
Wenn zum Beispiel a=2 und b=2 gewählt wird und es gilt i·dW =2 π, dann hat sich Punkt (X,Y) zweimal
um den Mittelpunkt gedreht.
In der gleichen Zeit dreht sich Punkt (x,y) nur einmal um den Mittelpunkt.
Man verbindet nun die zugehörigen Punkte (X,Y) mit (x,y) durch eine Strecke.
Im folgenden Sketch können Sie beobachten, wie dabei ein Bild entsteht.
Der Sketch ist so programmiert, dass man den Entstehungsprozess sehen kann. Das hat zur Folge,
dass die Anwendung relativ langsam läuft. Das spielt aber nur eine Rolle, wenn man mehr als 720 Punktepaare
berechnen lässt.
Für den Neustart des Sketches klicken Sie ins Bild !
Dann haben Sie folgende Möglichkeiten:
Taste:
- 'a' : Parameter a um eins erhöhen
- 'b' : Parameter b um eins erhöhen
- 'c' : Parameter a und b um eins erhöhen
- '+' : Anzahl der Punktepaare um 360 erhöhen
- 'f' : Wechsel zwischen schwarz-weiß und farbig
- 's' : Anhalten
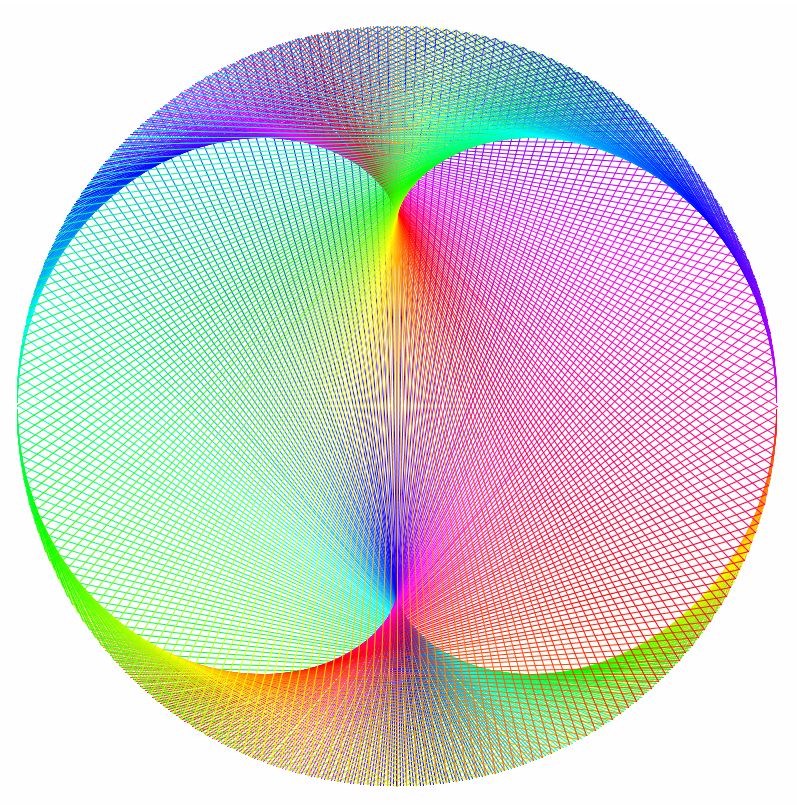
Bei Wikipedia finden Sie weitere Informationen zu den beiden Formen: Kardioide Nephroide .
Dort können Sie auch lesen, dass der Astronom Ole Roemer im 17. Jahrhundert bei der Suche nach der optimalen Form von Zahnrädern Kardioide untersucht hat. Aber noch viel früher untersuchten die Griechen die Kurve, die man erhält,wenn man einen Kreis um einen anderen rollen lässt und einen beliebigen Punkt des umlaufenden Kreises seine Bahnkurve aufzeichnen lässt. (Man erhält dann ebenfalls eine Kardioide.) Sie versuchten mit dieser Kuve die Bewegung der Planeten zu verstehen.
Wählt man a und b nicht gleich, so bekommt man, wie oben schon erwähnt,so bekommt man Lissajous-Figuren. Im folgenden Bild ist a=5, b=2 und es werden 1080 Punktepaare verwendet:

Der auf dieser Seite gezeigte Live-Sketch ist als Animation konzipiert. Bei jedem draw-Durchgang wird nur ein Punktepaar gezeichnet. So kann man den Entstehungsprozess gut beobachten. Wählt man per '+' Taste aber mehr als 720 Punktepaare, so wird die Animation sehr langsam. Um ein lückenloses farbiges Bild einer Epizykloide zu erhalten, sollte man aber mindestens 7200 Punktepaare berechnen lassen. Der Sketch "Epizykloide Schnell" erledigt diese Aufgabe in wenigen Sekunden. Die folgenden drei Bilder sind von oben nach unten: Kardioide, Nephroide und ein Bild mit a=6 und b=2. Danach folgen zwei Epizykloide, bei denen der Radius der beiden Kreise nicht gleich ist (r1=400 und r2=200):
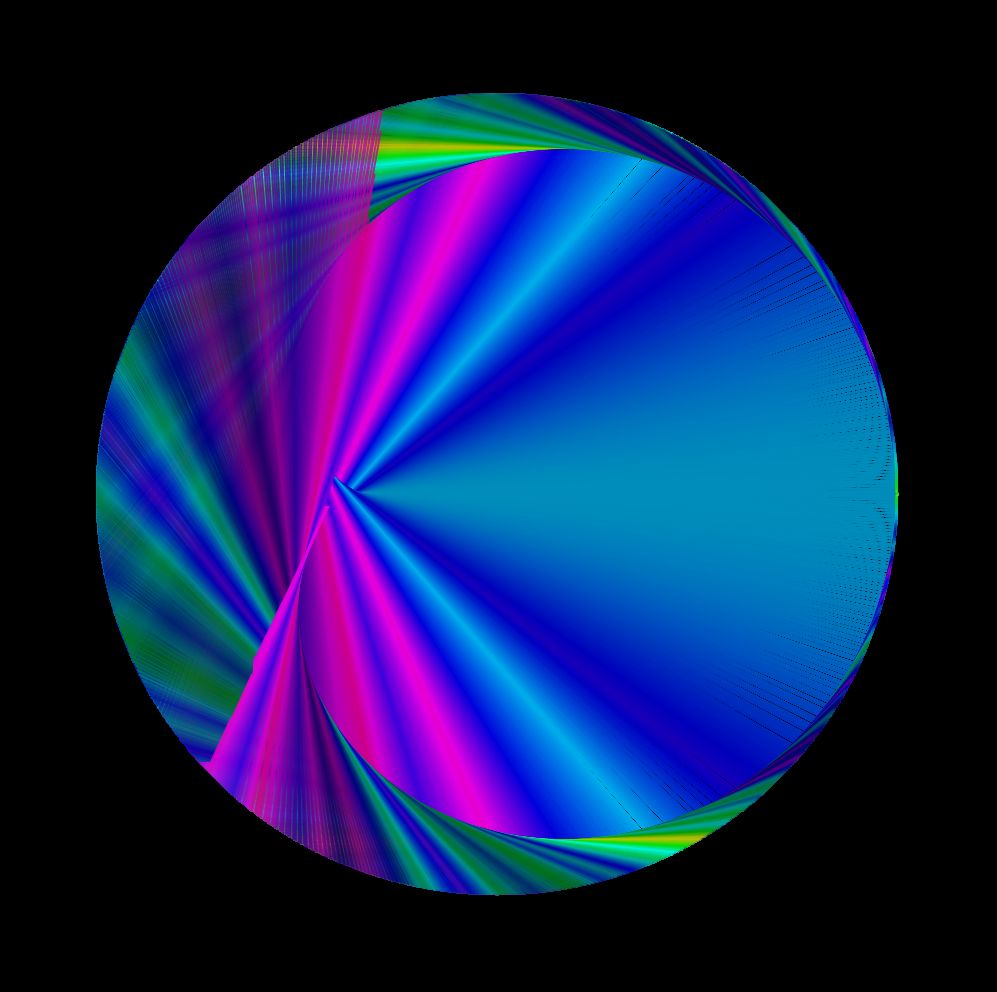
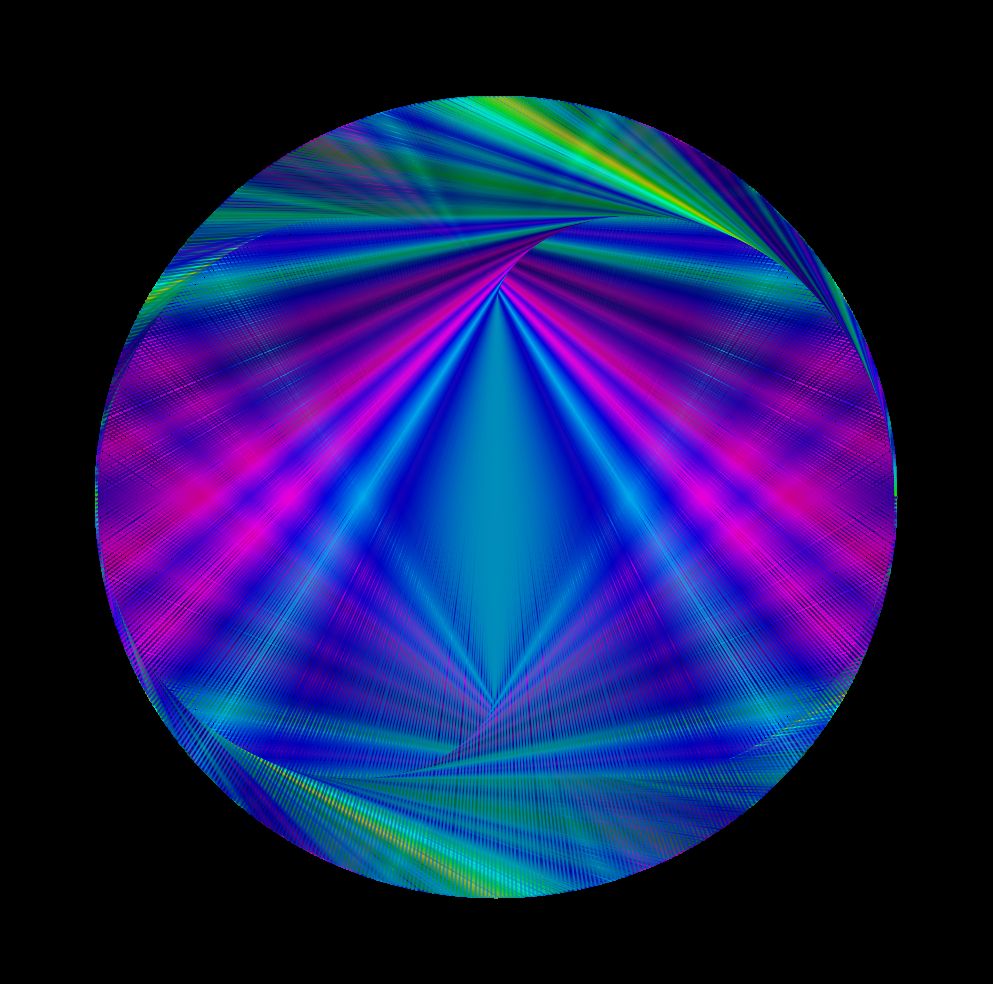


Epizykloide
Epizykloide Schnell
Menu