Menu

Nichtlineare dynamische Systeme

Im Lehrbuch behandelten wir das Beispiel eines Kometen, der mit vergleichbar sehr geringer Masse in das Schwerefeld von Sonne und Erde gerät. Dies ist ein Spezialfall des ansonsten nicht lösbaren Dreikörper-Problems. Wir veränderten kontinuierlich den Startpunkt und erkannten, dass zwei sehr nahe beieinanderliegende Startpunkte zu völlig verschiedenen Ergebnissen führen konnten. Und genau das ist das Kennzeichen nichtlinearer dynamischer Systeme. Ganz generell geht es beim Thema "dynamische Systeme" um alle Dinge, die sich mit der Zeit ändern. In aller Regel sind es aber Systeme, die nicht trivial zu beschreiben sind, wie das Wetter, Bewegung von Himmmelkörpern, mehrfach Pendel und zum Beispiel auch die Computersimulation "Game of Life". Es sind hauptsächlich zwei mathematische Verfahren, die man nutzt: Lösung von Differentialgleichungen und die Analyse von Iterationen. Folgende Begriffe werden Ihnen dabe begegnen: Choas,Ordnung, Attraktoren, Stabilität/Instabilität und der Schmetterlingseffekt.
Wir ändern die Iteration aus dem Lehrbuch nur an einer Stelle:

Ursprünglich wurde yNeu so definiert:
Das Phasendiagramm ändert sich dadurch fundamental. Die Iteration ist frei erfunden. Stellen wir uns aber vor, es handele sich um die Beschreibung einer zyklischen Bewegung einer Masse. Der Startpunkt des Körpers wird nach und nach verändert. Für jeden Startpunkt verfolgen wir die Iteration 1000 bzw 100 Mal. Und das mit 4000 verschiedenen Startpunkten. Den Parameter K deuten wir als Wert für äußere Versuchsbedingungen. Sie werden sehen, dass die meisten Trajaktorien den Körper aus der Bahn werfen (Winkelgeschwindigkeit und Radius werden immer größer).
In der Anwendung unten können Sie das Verhalten testen. Klicken Sie auf eine Stelle, die Sie vergrößert sehen wollen. Mit einem Klick in die linke untere Eckelinke untere Ecke erreicht man einen Neustart mit einem anderen Wert für K.
Zu jedem Startpunkt gehört eine Trajektorie. Da die Punkte innerhalb einer Trajektorie immer die gleiche Farbe hat, kann man erkennen, dass die feinen Linien in der Anwendung unten, zu verschiedenen Startpunkten gehören.



In den folgenden Bildern sind die Ergebnisse für acht verschiedene K-Werte zu sehen.




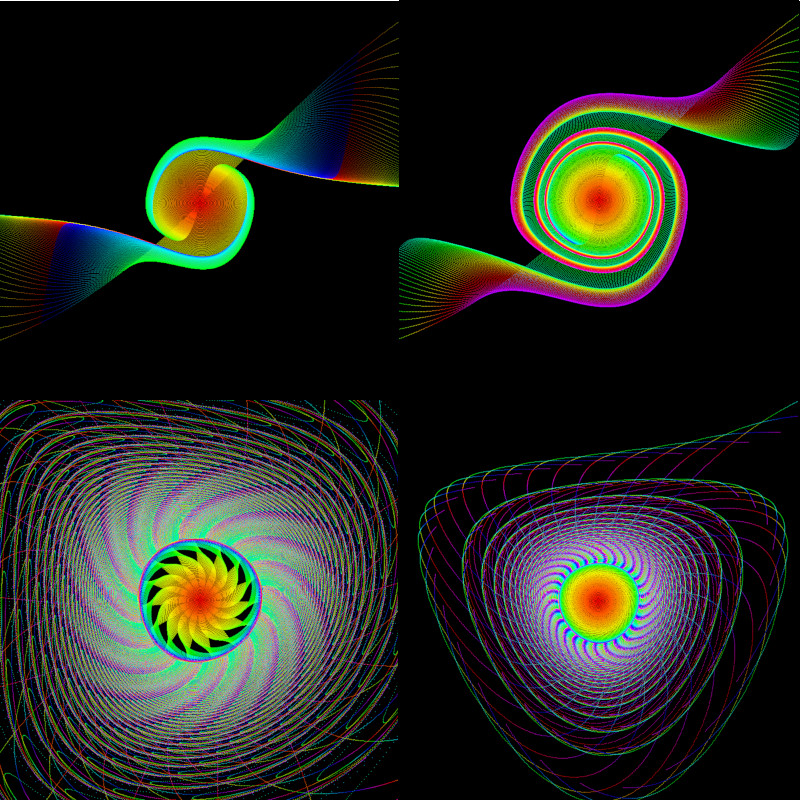
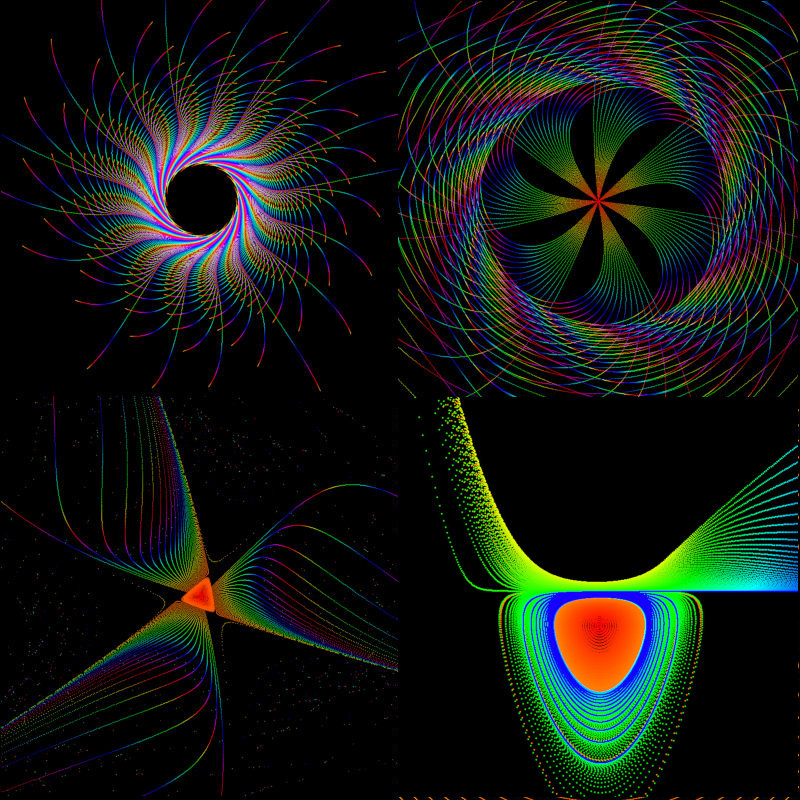
Mit der Taste 'f' lassen sich die Punkte dicker zeichnen. Beispiele im nachfolgenden Bild.





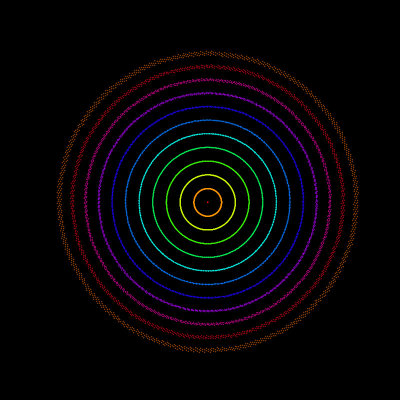
Unser Algorithmus liefert uns zweifellos eine Unmenge von hübschen Bildern. Wie aber müssten wir anhand eben dieser Bilder die Bewegung des Körpers interpretieren?
Eines ist sehr schnell klar: Die Bewegung wäre stark abhängig von den Anfangsbedingungen, also dem Winkel und der Winkelgeschwindigkeit zu Beginn. Der Außenbereich sieht zumindest mehr oder wenig chaotisch aus. In ihm landet man, wenn man die Winkelgeschwindigkeit am Anfang zu groß wählt. Was aber passiert eigentlich in der Nähe des Nullpunktes, also bei sehr kleinen Werten für Winkel und Winkelgeschwindigkeit? Im Bild links können Sie das überprüfen. Es wurden hier nur die ersten 12 Startwerte mit 1000 Punkten pro Trajektorie gezeichnet - die Vergrößerung erreicht man durch mehrfaches klicken auf das Ergebnis der obigen App. Die Linien werden zwar nach außen etwas breiter, aber dennoch erkennt man, dass sich Winkelgeschwindigkeit und Winkel so ändern, wie wenn sich ein Körper reibungsfrei in einem Kreis bewegt. (Kicked Rotator):

Sketch Dynamische Systeme.

Menu