Dynamische Systeme
Feigenbaum-Diagramm
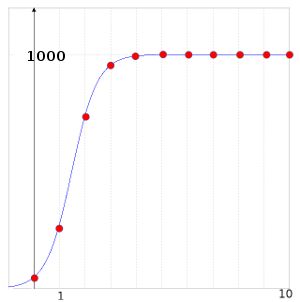
Exponentielles und beschränktes Wachstum beschreiben nur sehr unzureichend wie sich die Anzahl der Individuen einer Population entwickelt. Das logistische Wachstum liefert wesentlich glaubwürdigere Werte. Im Bild links könnte die zeitliche Entwicklung der Anzahl an Hasen auf einer Insel beschrieben sein. Schon nach 5 Jahren leben etwa 1000 Hasen auf der Insel und diese Zahl scheint sich nicht mehr zu verändern. Man kann sehr leicht selbst auf die Idee kommen, wie man aus der Anzahl der Hasen zu Beginn eines Jahres auf die zu erwartende Zahl am Ende des Jahres erhält. Zum einen ist Anzahl der Geburten in dem Jahr proportional zum aktuellen Bestand x. Zum andern aber ist die Nahrung beschränkt und daher ist die zu erwartende Anzahl auch proportional zu (1000-x). Auf 1 normiert bekommt man daher folgende iterative Formel:
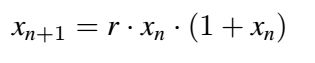
Sie sieht eigentlich ganz einfach aus. Probieren Sie es aus! Wählen Sie einen Wert für r zwischen 1,1 und 3,9 und rechnen Sie die ersten zehn Folgenelemente aus. Danach verwenden Sie einen anderen Wert für r und vergleichen ob die Entwicklung ähnlich verläuft.
Falls Sie aber keine Lust haben, zu rechnen, dann spielen Sie das Ganze grafisch durch. Im folgenden Bild sind die Schaubilder der Funktionen f(x) = rx(1-x) für drei Werte von r dargestellt. Starten Sie mit einem Wert von x zwischen 0 und 1 und markieren Sie den Funktionswert senkrecht darüber zum Beispiel auf dem blauen Schaubild. Dieser Wert muss nun erneut abgebildet werden. Dazu bewegen Sie sich bis zu Winkelhalbierenden und gehen von hier aus senkrecht nach oben oder unten zum Schaubild:
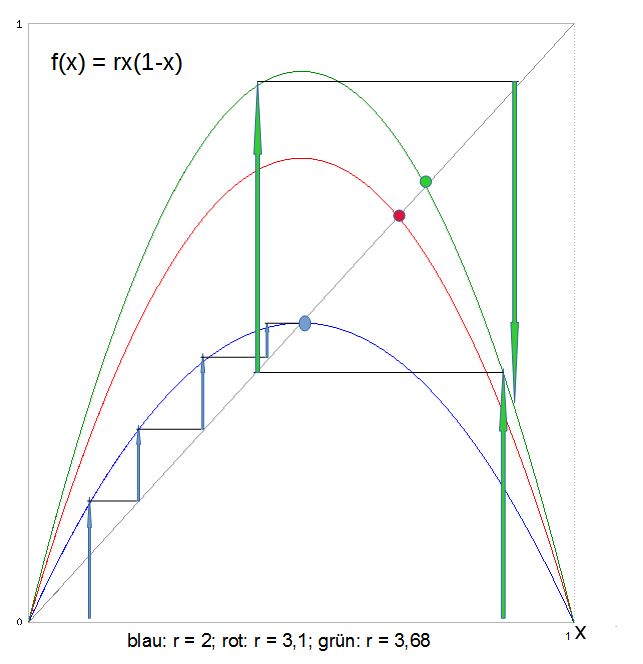
Klar ist, dass die Schnittpunkte der Parabeln mit der Winkelhalbierenden (g(x) = x) Fixpunkte der Abbildungen sind. Ist r kleiner als 3, scheint man sehr bald auf einen solchen Punkt zuzusteuern. Der im obigen Bild dargestellte Fall für r = 3,68 zeigt, dass mit minimal kleinerem Startwert, die Funktionswerte zwischen zwei Werten hin und her gesprungen wären. Die ersten 100 bis 200 Funktionswerte lassen sich natürlich auch recht einfach mit einem kleinen Programm bestimmen. Wir aber wollen auf möglichst bequeme Art herausfinden, ob es bei den Iterationen immer einen Grenzwert gibt. Oder springen die Funktionswerte immer zwischen zwei oder mehrern Werten hin und her?
Der Sketch feigenbaum, benannt nach Mitchel Feigenbaum (1975), soll zwischen r = 2,8 und r = 3,9 zunächst 500 Folgenelemente ausrechnen und danach für alle r-Werte dazwischen die nächsten 500 Werte senkrecht über r als x-Achse eintragen. Die Rechnung ist äußerst umfangreich, dennoch sollten Sie unten sehen, wie alle die Werte, einer nach dem anderen eingetragen werden. Es gibt ganz regelmäßige Bereiche, aber auch viele Stellen, bei denen die Folge sich zwischen zwei oder vier Werten nicht "entscheiden" kann. Erstaunlicher jedoch ist, dass bei vielen r-Werten ganz offensichtlich Chaos herrscht. Wenn Sie auf eine Stelle der Bildes klicken oder tippen, wird dieser Bereich wird zehnfach vergrößert.
Wenn Sie mehr über das Feigenbaum-Diagramm und die logistische Gleichung wissen möchten, finden Sie hier ausführliche Erklärungen:
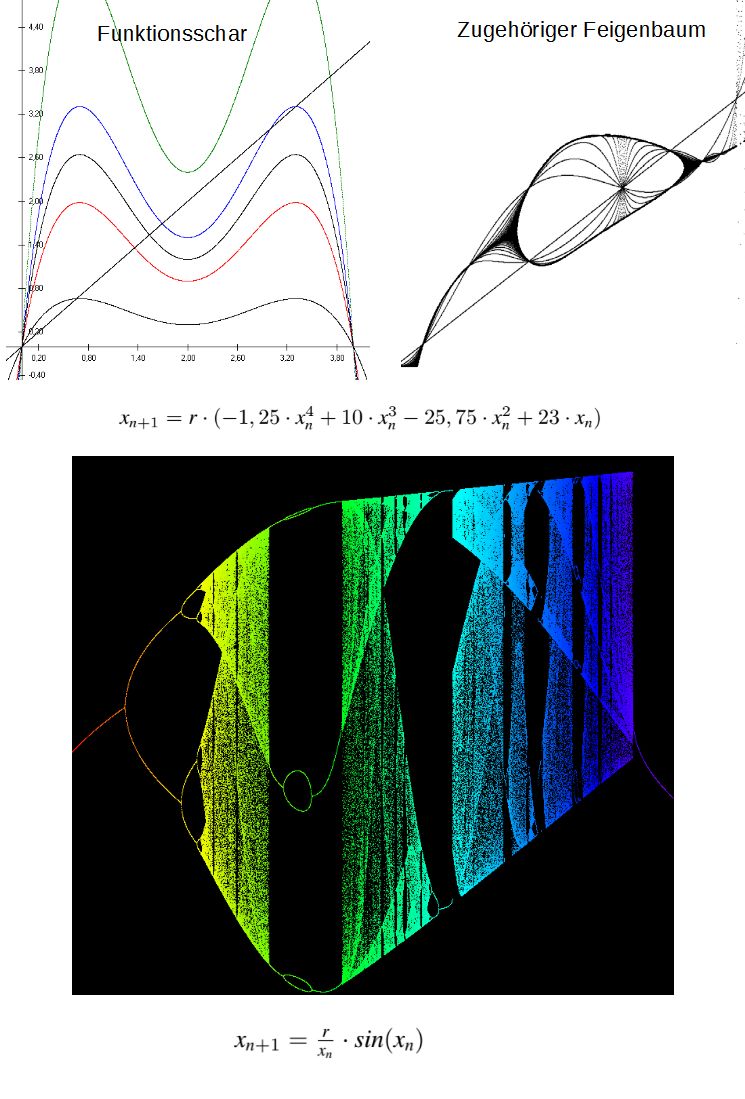
Logistische Gleichung Facharbeit über die logistischen GleichungNatürlich gibt es beliebig viele andere Funktionen (hier Iteratoren genannt), die ganz anders aussehende "Feigenbäume" erzeugen. Versuchen Sie selbst einige interessanten Fälle zu finden. Man muss sich dabei stets klarmachen, wie die Bilder für die Variable r entstehen. Am Anfang steht immer eine Schar von Funktion und die 1.Winkelhalbierende. Bleiben die iterierten Werte innerhalb bestimmter Grenzen? In welchem Bereich von r gibt es Ordnung, in welchem Chaos? Um Ihnen eine Idee zu geben, zwei Beispiel mit ihren Funktionen:
Das Feigenbaum-Diagramm ist relativ einfach zu verstehen. Daher kann man es für einen erster Einstieg in die Welt des Chaos verwenden. Wir werden in diesem und auch in anderen Kapiteln immer wieder darauf zurückkommen.
Sketch feigenbaum1.
Sketch feigenbaum2.
Sketch feigenbaum3.
Menu