Dynamische Systeme
Lyapunov-Exponent
Mit dem Feigenbaum-Diagramm kann man auf einen Blick das Verhalten der Iteration für beliebige r-Werte erfassen. Ist der Überblick nicht genau genug, zoomt man einfach ins Bild. Solange die verwendeten float - oder double-Werte mitmachen, kann man immer weiter und weiter eintauchen - und bekommt an manchen Stellen dennoch keine Klarheit über das Verhalten an eben dieser Stelle. Der Grund, weshalb wir uns mit dieser Materie befassen wollen, ist dass man mit Kenntnis des Lyapunov-Exponenten wunderschöne Fraktalbilder zeichnen kann...
Wann aber zeigt die betrachtete Iteration für einen Wert a ein solches (chaotisches) Verhalten? Schauen wir uns dazu einen zweiten Wert b an, der beliebig nahe an a liegt. Wir iterieren nun beide. In "ruhigen Gewässern" darf man erwarten, dass die erhaltenen Werte ebenfalls nahe beieinander liegen. Denken Sie an das Feigenbaum-Diagramm zum Beispiel bei r = 2,9. Ob man hier als Startwert a = 0,5 oder b = 0,55 wählt, spielt keine Rolle. Sie nähern sich beide dem einem selben Wert an. Das ist auch bei r = 3,1 so, obwohl hier zwei Werte alternierend angelaufen werden. Da dies aber sowohl für a, als auch für b gilt, kommen sich die iterierten Werte immer näher.

Der Mathematiker Alexander Lyapunov hat sich eine äußerst wirkungsvolle Methode ausgedacht, wie man feststellen kann, ob zwei beliebig nahe beieinander liegende sich im Laufe der Iteration von einander entfernen (dissipatives System) oder annähern (konservatives System). Die ersten drei Zeilen links geben die drei möglichen Fälle an, wie sich der Abstand zweier Werte von der n-ten zur (n+1)-ten Iteration ändern können. Im ersten Fall rücken die beiden Werte näher zusammen, im zweiten bleibt der Abstand gleich und im dritten Fall wächst der Abstand. Teilt man die linke (immer positive) Seite durch die rechte und nimmt danach den Logarithmus des Quotienten, so lässt sich über das Ergebnis L zumindest soviel sagen: L ist negativ, wenn die Werte sich annähern, Null, wenn der Abstand gleich geblieben ist und positiv, wenn der Abstand größer geworden ist. Natürlich besagt dieser einzige Übergang von der n-ten zur (n+1)-ten Iteration noch nicht viel. Nimmt man aber einfach den Mittelwert alle Übergänge bis N, dann bekommt man schon eher eine zuverlässige Information über das Verhalten an dieser Stelle (vorletzte Zeile). Bei beliebig kleinem Abstand der benachbarten Werte wird aus dem Quotient der Differenzen die Ableitung an der Stelle an
Im Sketch unten wurde der Wert des Lyapunov-Exponenten über das Bild des Feigenbaums gelegt. Die blaue Linie zeigt, wo λ den Wert Null besitzt. (Rechnerisch macht man es wie beim Feigenbaum-Diagramm. Die ersten z. B. 100 Folgenelemente bleiben unberücksichtigt. Danach rechnet man der Durchschnitt von 100 bis z. B. 800 ) Bei der ersten Gabelung des Feigenbaumdiagramms ist λ Null und somit stabil. Danach wird λ immer negativer. Eine derartige Stelle, an der der Wert für den Lyapunov-Exponent mit einer steilen Spitze nach unten läuft, nennt man "superstabil". Sobald wir im chaotischen Bereich angekommen sind, wechselt das Vorzeichen von λ und wird positiv. Dazwischen allerdings gibt es immer wieder negative Spitzen, die darauf hinweisen, dass es dort auch stabile Bereiche gibt. Klicken Sie in den Bereich, den Sie zoomen möchten. Sie werden feststellen, dass sich in diesem Gebiet Stabilität und Chaos abwechseln. (Wenn Sie mehrfach zoomen, dauert die Erstellung des Bildes eine Weile!)
Hier zwei Links, falls Sie mehr über dieses Thema wissen wollen:
Lyapunov-Exponent Chaos messen
Sie können sich den Verlauf des Lyapunov-Exponenten natürlich auch für andere Iterationen ausrechnen.
Im Bild unten wurde die Iteration f(x) = r*(-1.25*x4)+10*x3-25.75*x2+23*x verwendet.
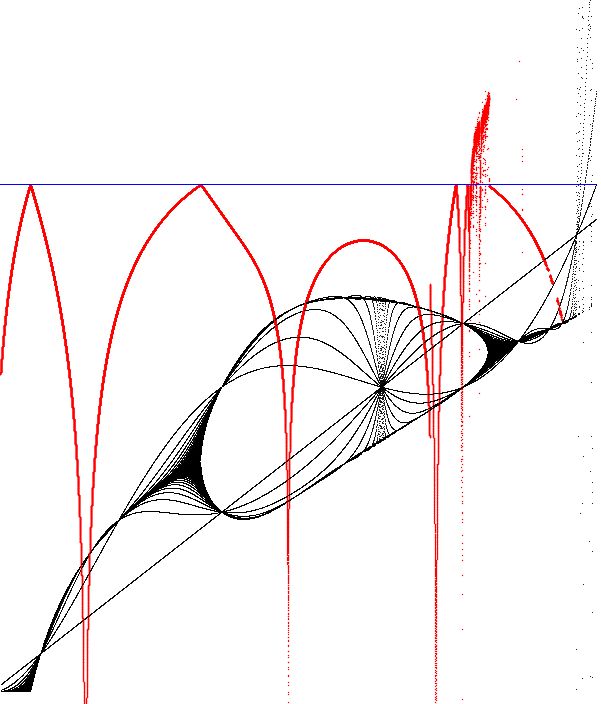
Sketch lyapunov1.
Sketch lyapunov2.
Menu