Dynamische Systeme
Zelluläre Automaten
Zur Begriffserklärung:
Wenn in einem dynamischen System die Anzahl der verschiedenen Inividuen durch eine endliche Menge natürlicher
Zahlen beschrieben wird, dann hat ein solches System einen diskreten Zustandsraum. Besitzt das dynamische System
einen diskreten Zustandsraum, dann spricht man von "zellulären Automaten".
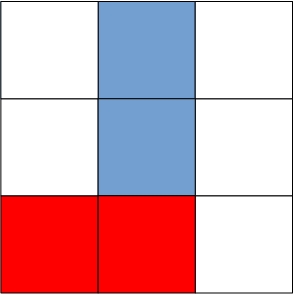
Hier behandeln wir einen zweidimensionalen zellulären Automaten in einer Räuber-Beute-Variante. In nebenstehendem Bild sieht man einen Ausschnitt der "Welt", bestehend aus Feldern, die entweder leer sind (weiß), von einem Hasen (blau) oder einem Fuchs (rot) besetzt sind. Anfangs wird die Belegung der Felder zufällig bestimmt. Man legt aber vorher fest, welchen prozentualen Anteil die verschiedenen Elemente haben sollen. Nach jedem Spielzug bewegt sich ein Element zufällig auf eines seiner acht Nachbarfelder (Moore-Umgebung). Was mit ihm danach geschieht, hängt davon ab, was zuvor auf dem Feld war.
Nun kommen die Regeln ins Spiel. Es ist einsichtig, dass ein von vielen Füchsen umgebener Hase gefressen wird. Andererseits werden auch die Füchse sterben, wenn es nicht mehr genug Hasen gibt. In der Animation unten würde ein Hasen (Zentrum Bild links), der zum Beispiel auf dem leeren Eckfeld oben links landet, sterben. Das heißt, das mittlere Feld und das Feld oben links ist danach leer. Die Regel, die hier greift, ist einfach: Ist in der Moore-Nachbarschaft nur ein oder kein Hase, dann stirbt er. Interpretation: Zu geringe Population führt zum Aussterben der Art.
Laden Sie sich den Sketch runter, und versuchen Sie alle Regeln zu finden. Verändern Sie die Regeln, um zu testen, wie man eine vermeiden kann, dass eine Art ausstirbt. Für einen Neustart laden Sie die Seite erneut.
Wenn Sie mehr über zelluläre Automaten, wie etwa das Game of Life wissen wollen, schauen Sie sich diese beiden Seiten an:
Game of Life Zelluläre AutomatenInteressant ist Beziehung der beiden Populationsgrößen. Man spricht hier von der Räuber-Beute-Beziehung. Das folgende Bild zeigt die Werte, die sich bei einem Programmstart mit 500 Bewegungen ergab. Rot zeigt die Anzahl der Füchse, blau die der Hasen. (Es gibt natürlich viel weniger Füchse als Hasen. Um die beiden Kurven besser miteinander in Beziehung zu bringen, wurden verschiedene y-Maßstäbe verwendet).
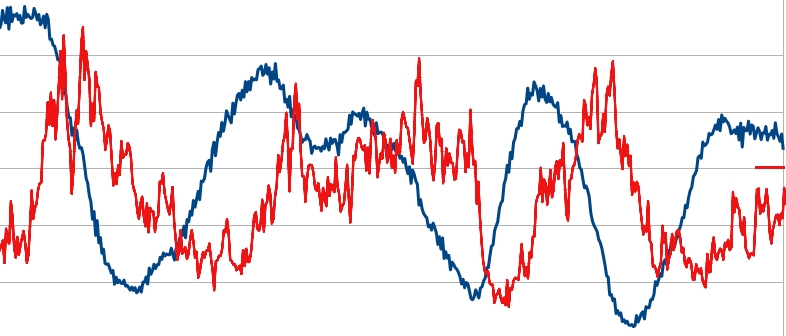
Man kann hier schön das in der Theorie geforderte Nachlaufen der Räuber-Kurve gegenüber der Beute-Kurve erkennen.
Unsere Sketch-Welt oben hat 10 0000 Felder. 10% davon sollen zufällig mit Hasen besetzt werden. Wieviele Möglichkeiten gibt es, die Hasen zu verteilen? 10 0000*9999*9998*.....*9002*9001. Das ist eine Zahl mit sehr vielen tausend Stellen. Das heißt, sowohl die Anfangssituation als auch der Verlauf der Entwicklung wird niemals gleich sein...
Sketch zellAutomat.
Menu