Julia Fraktale Spezial: Multi Fraktale
Neu im letzten Abschnitt war, dass mehrere Picard-Iterationen pro Iterationsschritt ausgeführt wurden. Dies führte zu neuen Bildergebnissen. Eine weitere Möglichkeit ganz neue Julia Fraktale zu erzeugen bietet sich an, wenn man statt mehrerer verschiedener Piccard-Iterationen hintereinander, jede komplett zuende rechnet. Wenn man also für einen Punkt eine erste vorgegebene Julia-Iteration bis zum Verlassen der Schleife berechnet und danach in eine zweite Schleife mit der nächsten Iterationsformel weitermacht. Schauen wir uns zum besseren Verständis den Processing-Code dafür an:
......................................
while (N < maxiterations) {
z0 = Q(zAlt,M,C,qH);
zNeu = z0;
laenge =zNeu.getLength();
if(laenge > massFuerUnendlich ) {break;}
zAlt = zNeu;
N++;
}
zAlt = Z0;
while(N < 2*maxiterations){
z1 = zAlt.multiply(1-r).addC(zAlt.multiply(r));
z1 = Q(z1,M,C,qH);
zNeu = z1;
laenge =zNeu.getLength();
if(laenge > 2*massFuerUnendlich ) {break;}
zAlt = zNeu;
N++;
}
zAlt = Z0;
......................................
Die Zeilen zur Bestimmung von Winkel- und Streckensumme wurden der besseren Überschaubarkeit wegen weggelassen.
Was hier für zwei Fraktale dargestellt wurde, lässt sich auf im Prinzip beliebig viele erweitern. Beschränken wir
uns aber auf die schon bekanten vier Iterationen (siehe Abschnitt "Multi-Picard Iterationen").
Das folgende Bild ist ein Beispiel für den Fall, dass man nach der oben angedeuteten Art, alle vier Fraktale einbezieht: while (N < maxiterations) {
z0 = Q(zAlt,M,C,qH);
zNeu = z0;
laenge =zNeu.getLength();
if(laenge > massFuerUnendlich ) {break;}
zAlt = zNeu;
N++;
}
zAlt = Z0;
while(N < 2*maxiterations){
z1 = zAlt.multiply(1-r).addC(zAlt.multiply(r));
z1 = Q(z1,M,C,qH);
zNeu = z1;
laenge =zNeu.getLength();
if(laenge > 2*massFuerUnendlich ) {break;}
zAlt = zNeu;
N++;
}
zAlt = Z0;
......................................

Weder die Anzahl der hintereinander zu berechenden Fraktale, noch die Art der Fraktale sind vorgegeben. Die folgenden Bilder zeigen einige Beispiele in allen möglichen Varianten. Man erkennt nicht, dass die Entstehung dieser Bilder im Prinzip auf dem üblichen Julia-Algorithmus beruht:

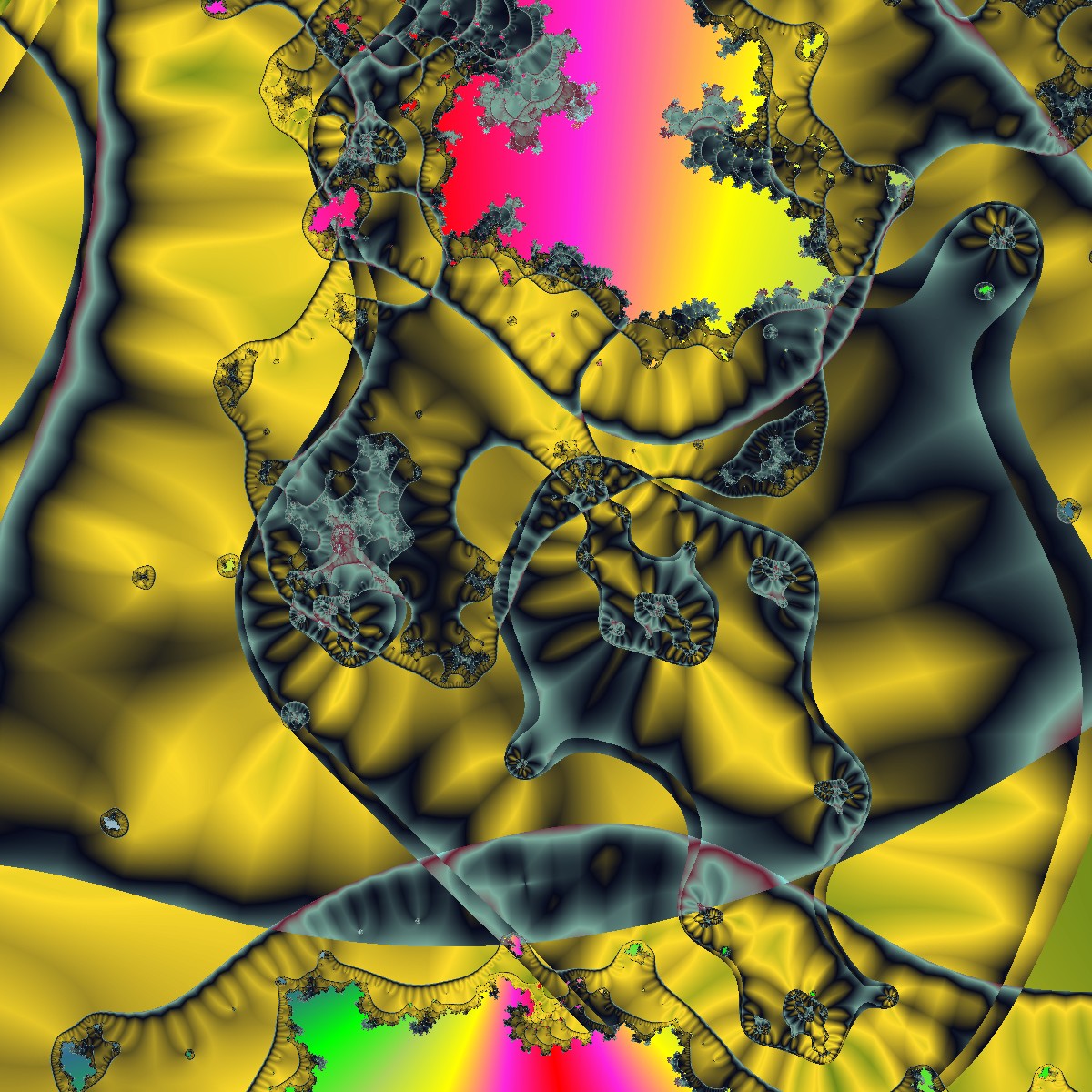
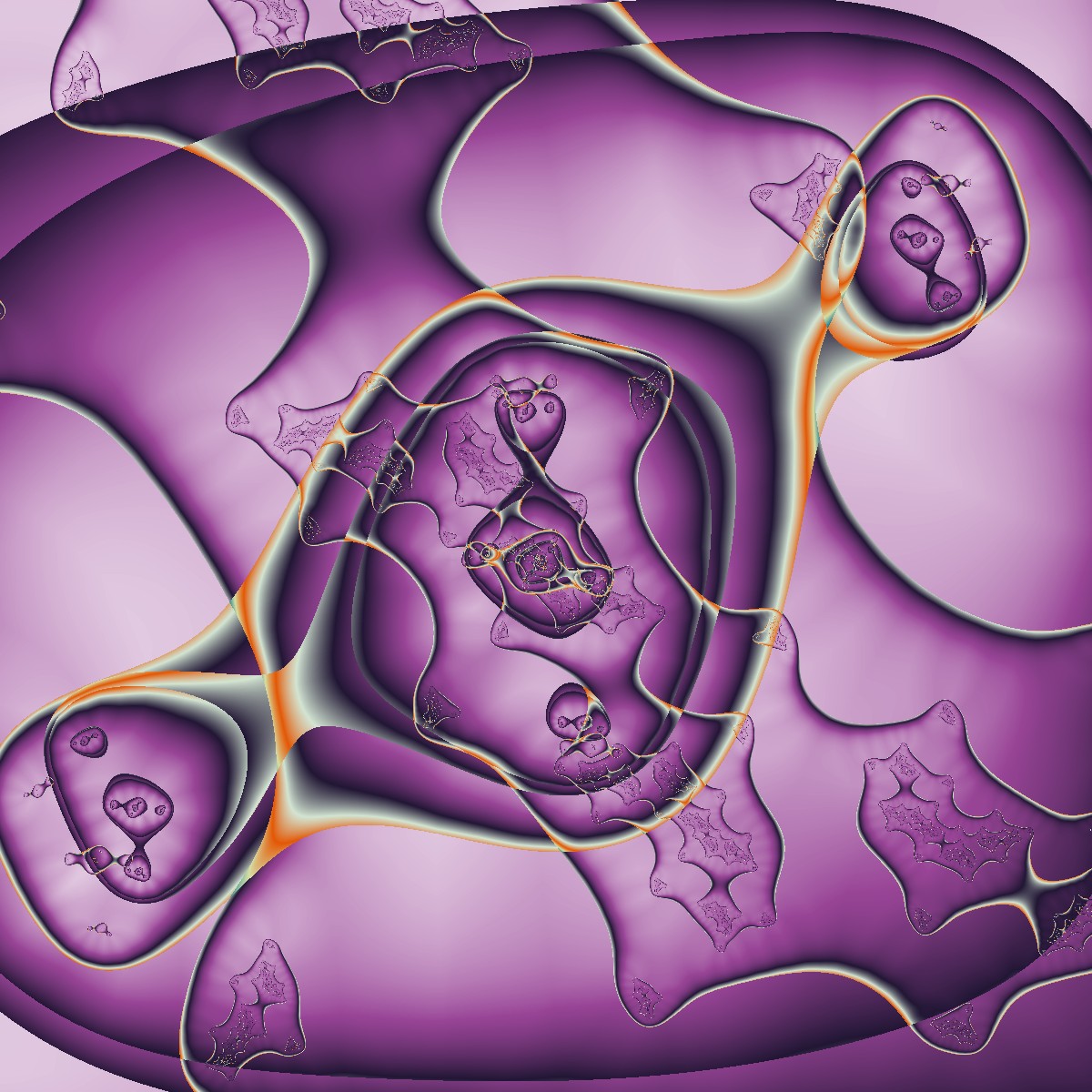
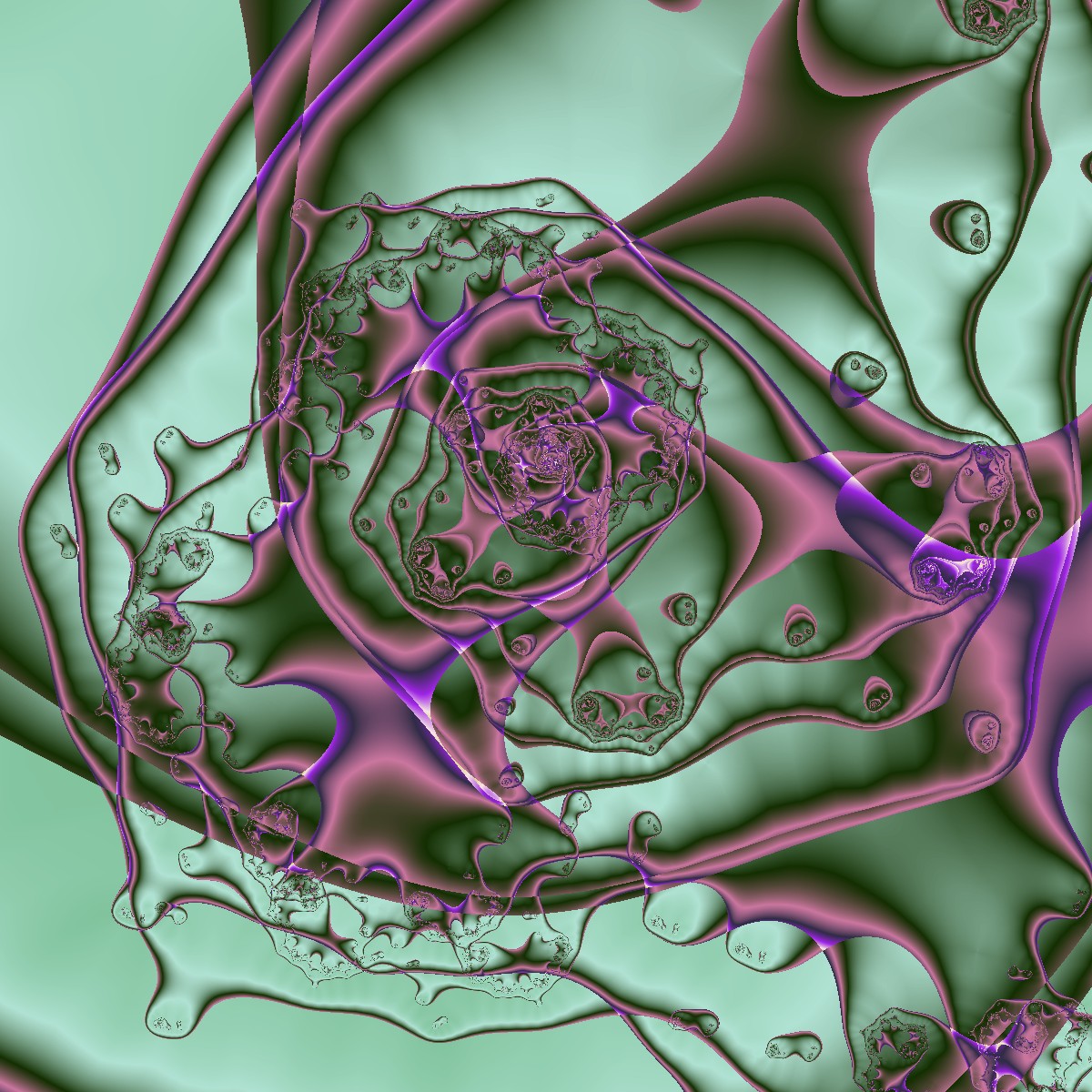
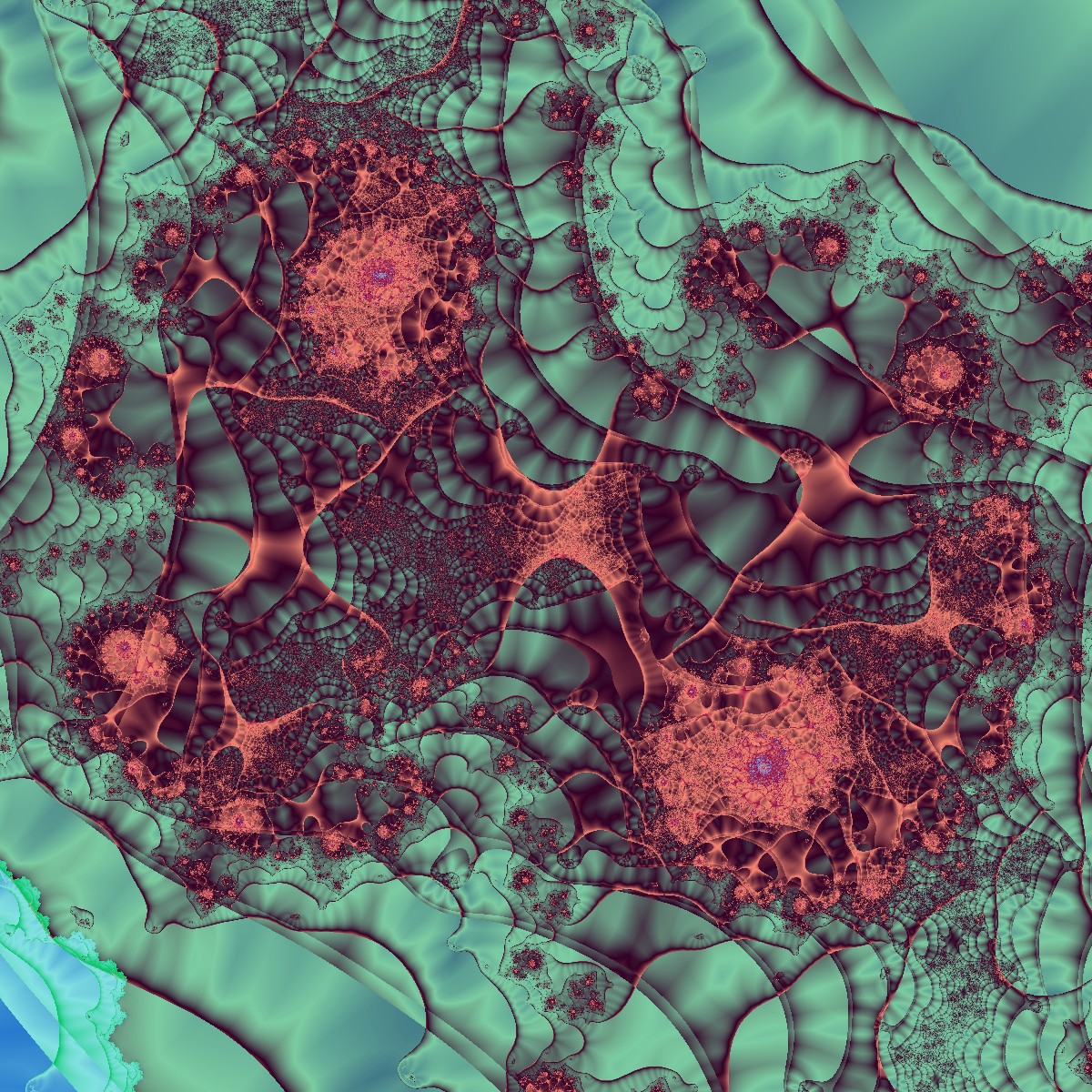
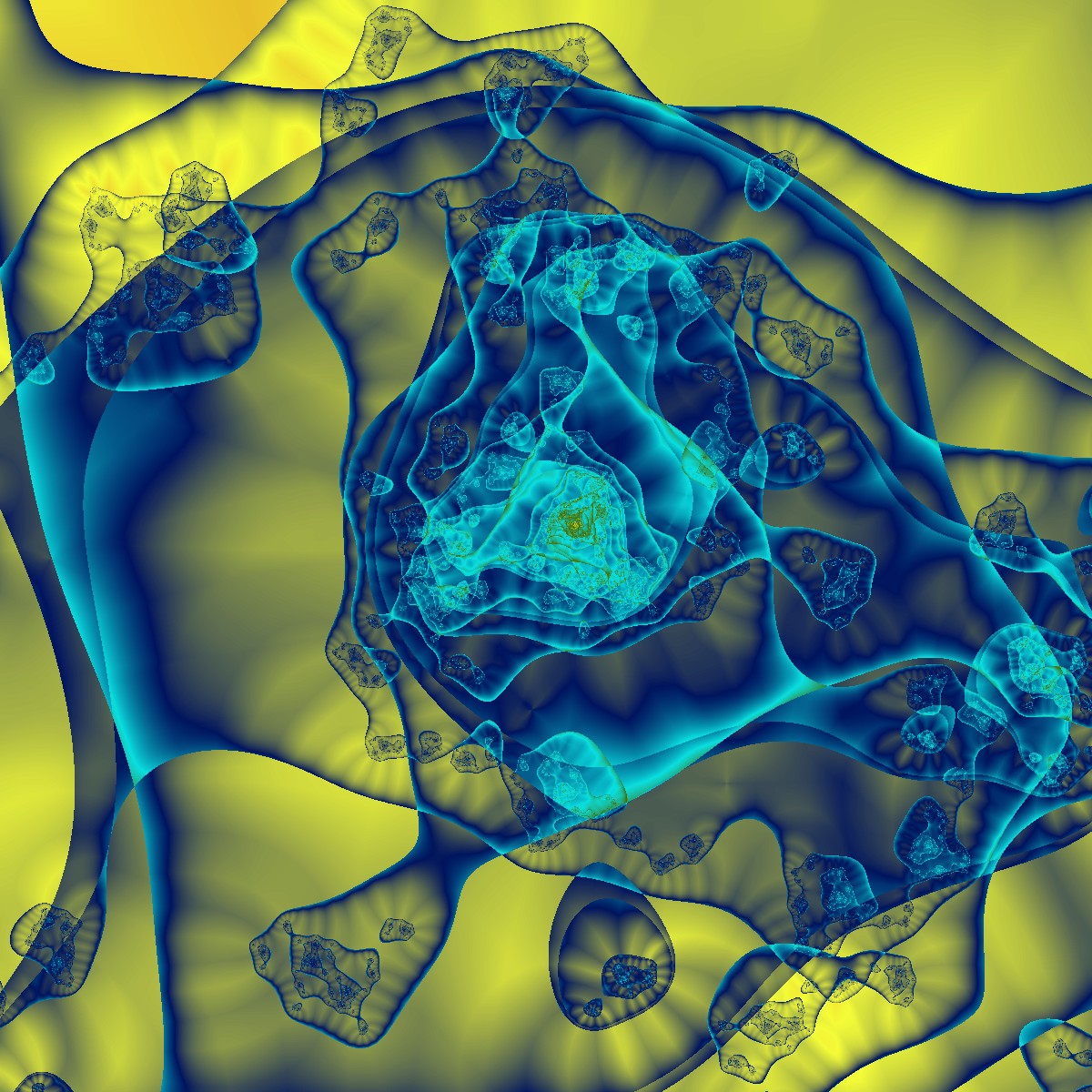
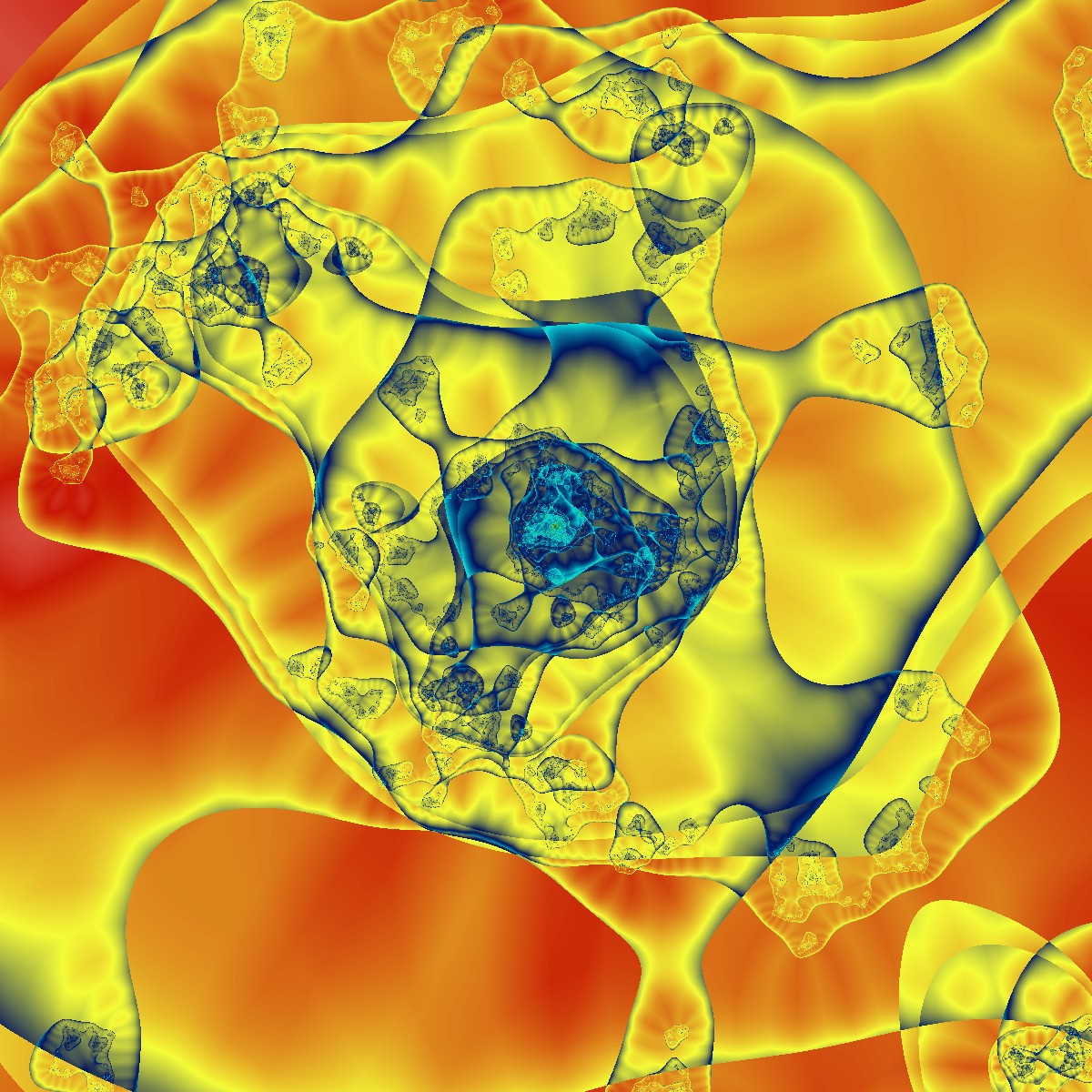



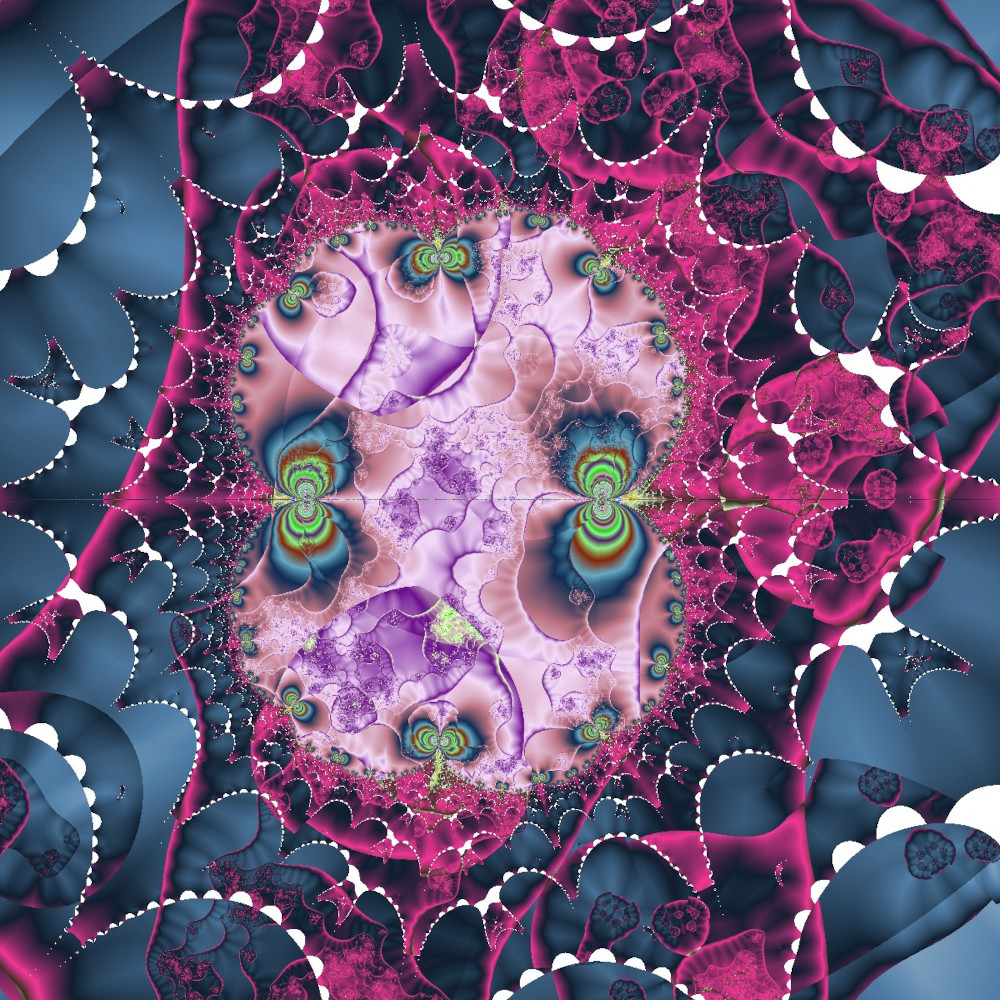

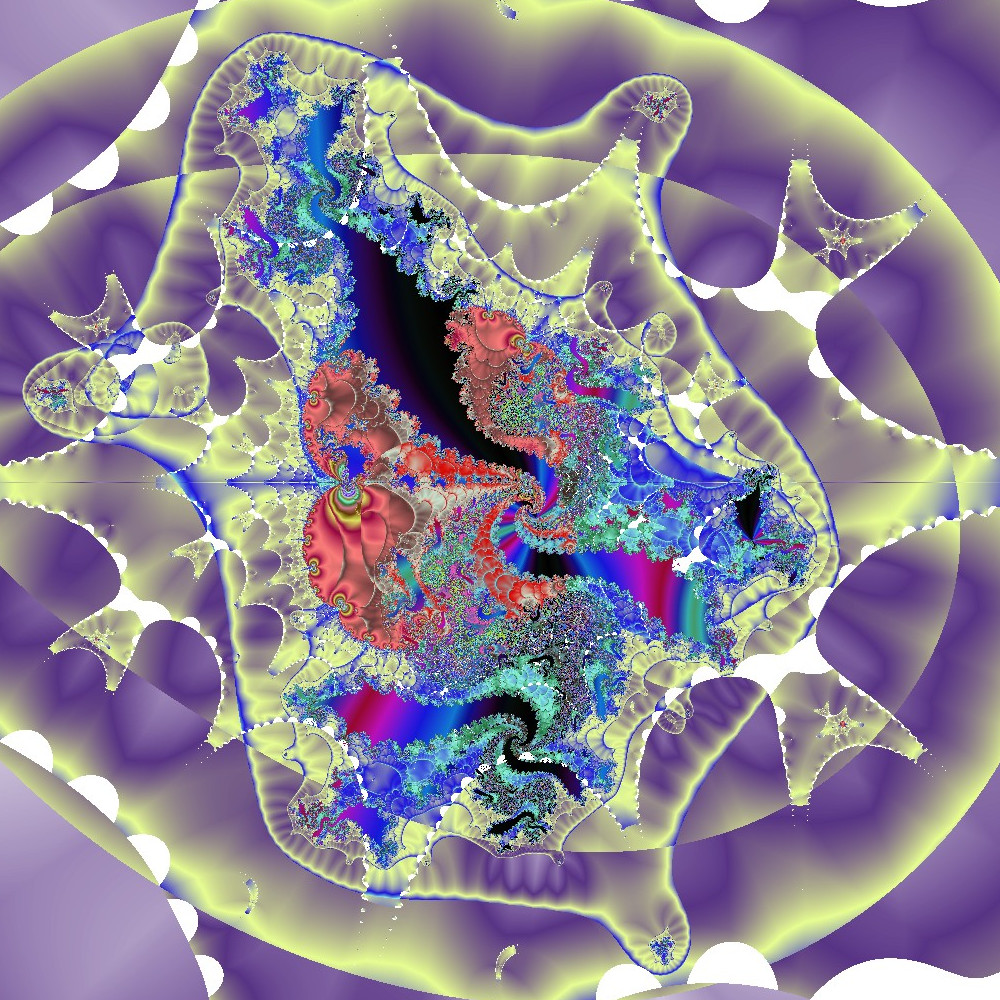

Julia Fraktale Spezial Multi Fraktale
Menu