Julia Fraktale Spezial: Multi-Picard Iteration
Die üblichen Julia Fraktale sind hinreichend bekannt, und nicht erst seit gestern.
Leider ist es so, dass nur vergleichsweise wenige c-Werte zu komplexeren Bildern führen. Das liegt daran, dass
bei den übrigen c-Werten nur 2 bis 3 Mal iteriert werden muss, bis der Fluchtkreis verlassen wird.
Damit kann man nun wirklich keine farbigen Übergänge schaffen.
Abhilfe schaffte zunächst die zusätzliche Verwendung von Strecken- und Winkelsummen. Diese Möglichkeit haben wir im
letzten Abschnitt ausführlich behandelt.
Und in der Tat, konnten wir nun auch für weniger geschickte c-Werte ganz ordentliche Bilder
erzeugen. Aber noch immer gibt es bei zufälliger Wahl der Parameter zu viele unbedeutende Bildergebnisse.
Das "Spezial" in der Überschrift soll darauf hinweisen, dass in diesem Abschnitt des Fraktal-Kapitels andersartige
Fraktale erzeugt werden sollen. (Winkel- und Streckensummen werden beibehalten).
Zusätzlich nutzen wir Iterationen in mehreren Stufen:
Zur Erzeugung eines Julia-Fraktals benötigt man zunächst eine Iterationsvorschrift, wie zNeu = f(zAlt). In der
Fixpunkttheorie wird sie Picard Iteration genannt. Diese muss nicht aus einer einzigen Vorschrift bestehen.
Ein Beispiel:
zNeu0 = fn(zAlt))
zNeu1 = H(zNeu0)
zNeu2 = I(zNeu1)
zNeu3 = K(zNeu2)
Man kann die Bestimmung von zNeu nun variabel gestalten, indem man festlegt, bei welchem der Werte zNeu0, zNeu1, zNeu bzw. zNeu3
gestoppt werden soll.
Die sogenannte Mann-Picard Iteration besteht aus zwei Vorschriften, die Ishikawa-Iteration aus drei
und die Noor-Iteration aus vier Vorschriften. Allen gemeinsam ist, dass sie die Erzeugung eines Julia-Fraktals
mehr oder weniger beschleunigen. Hier verwenden wir ein Verfahren, das von Jalaoso und Khan vorgeschlagen wurde.
Es ist den drei zuvor genannten, was die Geschwindigkeit angeht, überlegen. Und so sieht die Iteration aus:
z1 = fn((1-r) ⋅zAlt + r ⋅ fn(zAlt));
z2 = fn((1-s) ⋅z1 + s ⋅ fn(z1));
z3 = fn((1-t) ⋅z1 + t ⋅ fn(z2));
zNeu = fn(z3);
Alle Funktionen fn sind hier so definiert:
fn(zNeu) = zAltn + zAlt2 + m ⋅ zAlt + c ;
zAlt, m, c ∈ ℂ; n ∈ ℕ; n> = 2; r,s,t ∈ ]0;1]
Weshalb ist diese Iteration vorteilhaft? Jalaoso und Khan haben eine Formel bewiesen,
die, in Abhängigkeit der obigen Parameter, einen Radius errechnet, ab der die Folge mit Sicherheit divergiert.
So kann es sein, dass man zum Beispiel nur 5 Iterationen berechnen muss,
und trotzdem sicher sein kann, dass die Folge beim gewählten Startpunkt divergiert. Zum Zeichnen eines attraktriven
Fraktals ist dies jedoch nicht unbedingt von Vorteil. Die Farbdifferenzierung leidet ganz erheblich, wenn nur so
wenige Werte, die das Verlassen der Iteration festhalten, zur Verfügung stehen. Arbeitet man bei der Auswertung
der Iteration ohne Winkel- und Streckensumme, so ist das Ergebnis fast immer enttäuschend.
Im Abschnitt "Julia versus Mandelbrot" des Kapitels haben wir festgestellt, dass die gewöhnlichen Julia -Fraktale
einen c-Wert haben müssen, der vom Rand der Mandelbrotmenge stammt. Daher bauen wir in den Sketch die Möglichkeit
ein, dass mit den gegebenen Werten eine transparente derartige Menge eingezeichnet wird. Klickt man nun rechts auf
eine Randstelle der Menge, so wird dieser c-Wert übernommen und die Julia-Fraktale sehen deutlich besser aus.
Wenn Sie den Sketch weiter unten herunterladen, dann schauen Sie sich vor allem die keyPressed Events an.
Mit ihnen lassen sich die Fraktale feinabstimmen. Mit linker Maustaste zoomt man auf die angeklickte Stelle, mit der
rechten Maustaste wird der angeklickte Punkt als c-Wert in der Iteration verwendet.
Eine Frage sollte noch beantwortet werden: Wie unterscheiden sich die Fraktale, abhängig davon, an welcher Stelle
man die Iteration verlässt? Das folgende Bild zeigt von links nach rechts und von oben nach unten die vier verschiedenen
Ergebnisse:
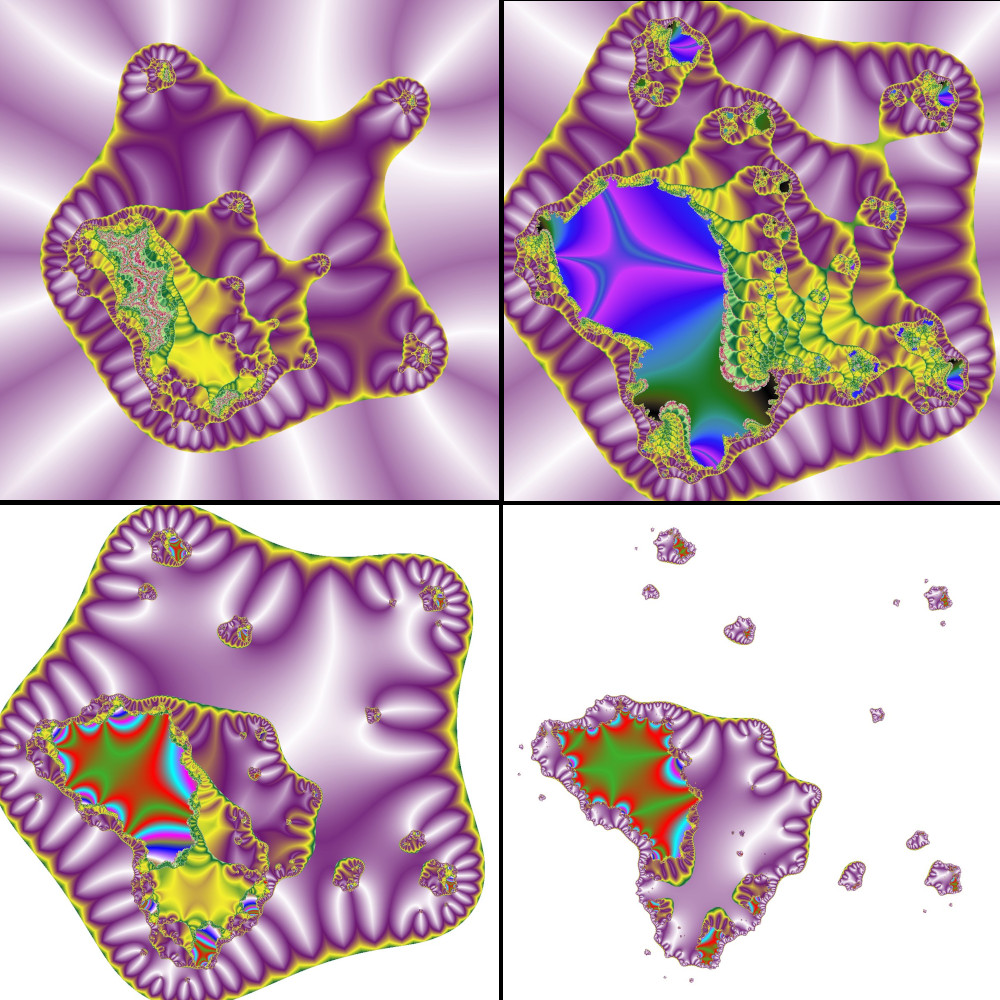
Die Parameter oben sind alle gleich, lediglich der Ausgang aus der Iteration ist verschieden. Unten rechts befindet
sich das Ergebnis für den Ausgang nach vier Schritten. Offensichtlich gibt es wesentlich weniger Punkte, die sich
nach der vorgegebenen maximalen Anzahl von Iterationsschritte noch innerhalb des Fluchtradius befinden.
Die Bilder, die mit diesem Sketch erzeugt werden können, sind deutlich verschieden von den gewöhnlichen
Julia Fraktalen. Lässt man allerdings die Winkel- und Streckensummen weg (Bild unten rechts), so bekommt man nichts wirklich Neues.
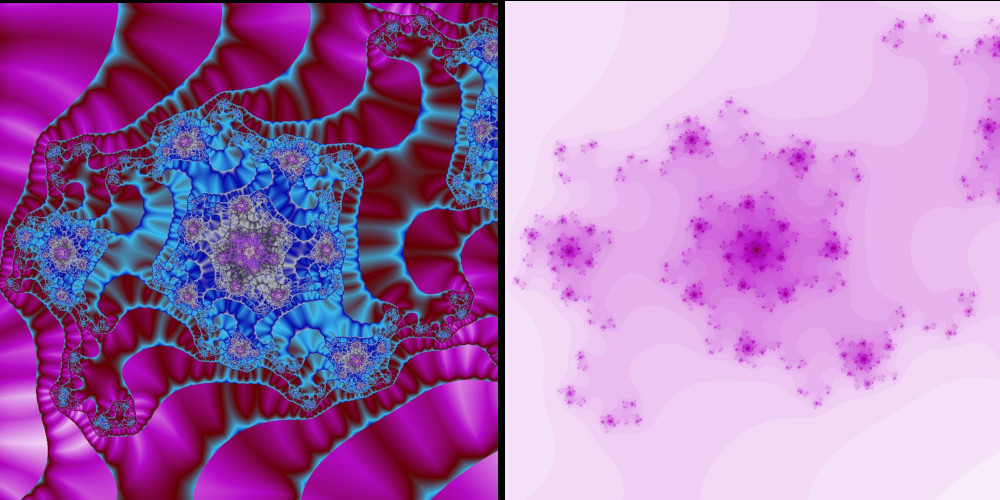
Natürlich kann man die obigen Gleichungen beliebig verändern. Fügt man beispielsweise eine Sinus-Funktion ein, kann
man ein solches Bild erhalten:

Hier einige Beispiele mit den obigen Gleichungen:









Menu