Fraktale: Fallen (Traps) 1
Wozu Fallen aufstellen?
 Um Julia-Fraktale zu zeichnen, beobachtet man für jede Zahl eines Bereiches der komplexen Ebene
beispielsweise maximal 250 Iterationen. Zuvor wählt man einen Radius R um den Ursprung.
Wird der Kreis verlassen, gehen wir davon aus, dass die Folge divergent ist. So bietet sich etwa R = 500 an.
Man färbt nun den Startpunkt entspechend der Anzahl der Iterationen, die für das Verlassen des Kreises nötig waren.
Der Startwert ist dabei der konstante Wert c in der Iterationsformel.
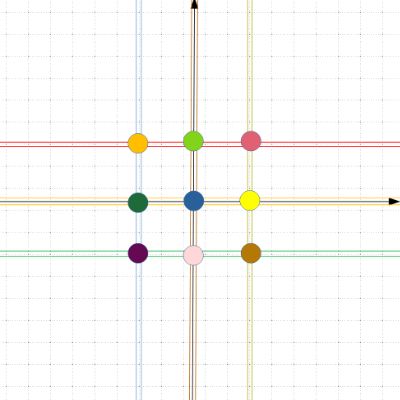
Nun kann man einen Kreis oder ein anderes abgeschlossenes
Gebiet (die Falle!) innerhalb der Definitionsmenge festlegen. Fällt während der Iteraion ein Punkt in das Gebiet,
so wird die Iteration gestoppt. Der Startwert wird dann nach einer in der Falle gültigen Regel eingefärbt. Wenn die
Falle ein Kreis ist, so wird eine dieser Falle zugeordneter Farbe verwendet, wobei man, um dabei einen 3D-Effekt
zu erhalten, den Abstand vom Mittelpunkt bestimmen und die Helligkeit
um so größer wählt, je geringer der Abstand zum Mittelpunkt ist.
Um Julia-Fraktale zu zeichnen, beobachtet man für jede Zahl eines Bereiches der komplexen Ebene
beispielsweise maximal 250 Iterationen. Zuvor wählt man einen Radius R um den Ursprung.
Wird der Kreis verlassen, gehen wir davon aus, dass die Folge divergent ist. So bietet sich etwa R = 500 an.
Man färbt nun den Startpunkt entspechend der Anzahl der Iterationen, die für das Verlassen des Kreises nötig waren.
Der Startwert ist dabei der konstante Wert c in der Iterationsformel.
Nun kann man einen Kreis oder ein anderes abgeschlossenes
Gebiet (die Falle!) innerhalb der Definitionsmenge festlegen. Fällt während der Iteraion ein Punkt in das Gebiet,
so wird die Iteration gestoppt. Der Startwert wird dann nach einer in der Falle gültigen Regel eingefärbt. Wenn die
Falle ein Kreis ist, so wird eine dieser Falle zugeordneter Farbe verwendet, wobei man, um dabei einen 3D-Effekt
zu erhalten, den Abstand vom Mittelpunkt bestimmen und die Helligkeit
um so größer wählt, je geringer der Abstand zum Mittelpunkt ist.
Im Bild links sind insgesamt 15 Fallen aufgestellt. Wenn ein Punkt in einer streifenförmigen Falle gefangen wird, so
bestimmt der Abstand zur Mittellinie die Helligkeit des Farbtons. So kann man erreichen, dass der Farbton in der Mitte
des abgebildeten Bereichs etwas heller ist, als am Rand.
Natürlich hat dieses Verfahren keinerlei mathemtischen Wert. Es geht allein um die Erzeugung ästhetischer Bilder!
Das "Geheimnis" besteht daher nicht nur in der Iterationsformel sondern auch in der Wahl der Fallen und deren
farblichen Auswirkungen. Ein Hinweis: Wählen Sie die Fallen nicht zu groß!
Nachfolgend finden Sie einige Beispiele inklusive zugehöriger Sketche. Beachten Sie, dass, wie schon zuvor, ein Linksklick mit
Faktor 5 in das Bild zoomt. Ein Rechtsklick legt den konstanten Wert c für das Julia-Fraktal fest. Weil interessante
c-Werte nur an den Rändern des Mandelbrot-Fraktals zu finden sind, kann man mit Taste m ein Mandelbrot-Fraktal
zeichnen. Sehen Sie sich den Quellcode an, wenn Sie wissen wollen, welche weitere Funktionen die Sketche liefern.
Gitter-Kreise-Traps für Julia-Fraktale
Im ersten Beispiel werden "Fallen" ähnlich obigem Bild benutzt. Es sind aber im Gegensatz zu oben hier acht Gitterlinien und sechzehn Kreise in den Schnittbereichen der Gitterlinien. Die Farbtafel-Klasse lässt unzählige Einfärbungen zu. Experimentieren Sie auch mit anderen Farbzuordnungen. Die im Sketch benutzte Iteration für das Standard-Julia-Fraktal (z -> z2 + c mit erstem Bild) sollte ebenfalls variiert werden (z.B.: z -> z3 + c mit zweitem Bild).

Julia2TrappedGitterKreise

Julia3TrappedGitterKreise
Ringe-Kreise-Traps für Julia-Fraktale
Im zweiten Beispiel bestehen die Fallen aus mehreren konzentrischen Ringen und acht Kreisen. Die im Sketch benutzte Iteration für die Julia-Fraktale sind: z -> z3 + c und z -> z4 + c
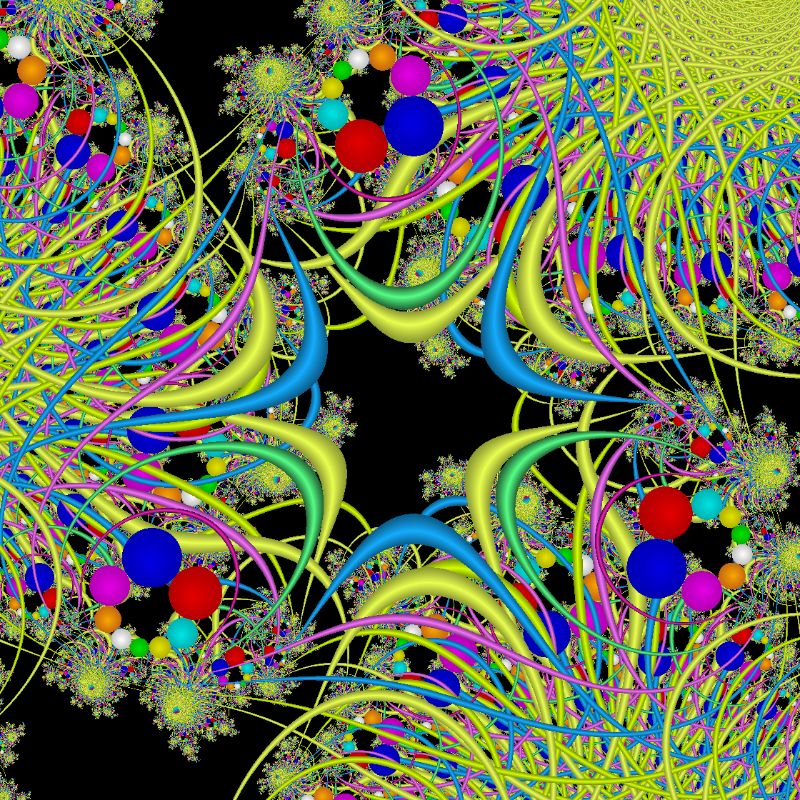
Julia3TrappedRingeKreise

Julia4TrappedGitterKreise
Menu