Winkel- und Streckensummen Färbung
Bisherige Methode
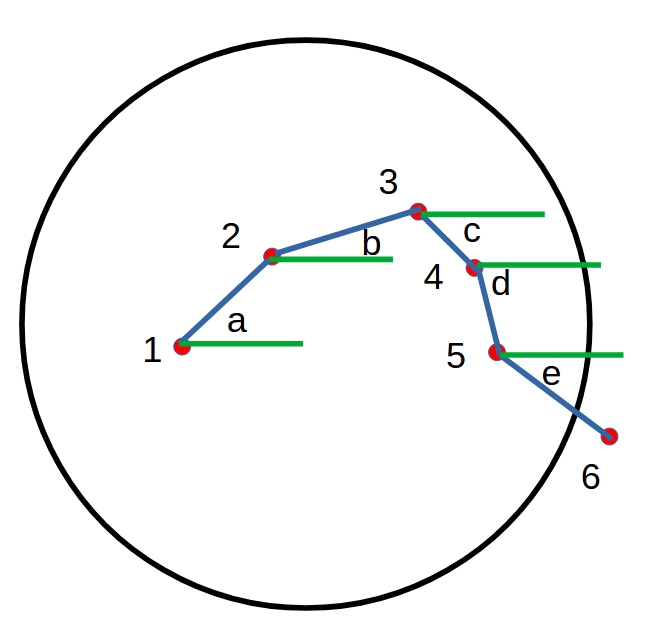
Die Farbe kam dadurch zustande, dass man für jeden Punkt des Definitionsbereichs
der komplexen Ebene überprüfte, wie viele Iterationen mit diesem Punkt als Anfangswert nötig waren, bis ein festgelegter Bereich verlassen wurde.
Im obigen Bild wäre dies die Zahl 6, die dann auf eine bestimmte Farbe der Farbpalette zeigt, mit der das Pixel,
das eben dieser komplexen Zahl entspricht, bei Punkt 1 gefärbt wird.
Das Problem dabei: selbst bei großen Radien kommt man mitunter kaum auf genügend hohe Werte, die einen
glatten Farbverlauf erlauben.
Andere Möglichkeit
Eine deutlich stärkere Farb-Differenzierung bekommt man, wenn man zusätzlich die gesamte Streckenlänge und die Summe
der Differenzbeträge der Winkel zur waagrechten Achse (im Bogenmaß) mit bewertet. Um keine Farbsprünge zu erhalten, verwenden
wir nur positive Katheten bei der Berechnung des Winkels. Da die Summe der Winkel deutlich kleiner
sein dürfte als die Gesamtstrecke, wird die Winkelsumme noch mit einem geeigneten Faktor multipliziert. Die Julia-Iteration
kann dann so aussehen:
Aalt = 0; Balt = 0;
zAlt = Z0;
int n = 0;
double SL=0;
double SW=0;
while (n < maxiterations) {
zNeu = zAlt.multiply(zAlt);
zNeu = zNeu.addC(C);
laenge =zNeu.getLength();
if (laenge > massFuerUnendlich) {
break; // Bail
}
SL = SL + zAlt.subtractC(zNeu).getLength();
A = abs((float)zNeu.re);
B = abs((float)zNeu.im);
Wneu = inversTangens(A,B);
Aalt = abs((float)zAlt.re); // A
Balt = abs((float)zAlt.im); // A
Walt = inversTangens(Aalt,Balt); // A
dW = abs(Wneu-Walt); // A
SW = SW + dW;
zAlt = zNeu;
n++;
}
SW = 100*SW;
n = n+round((float)(SW+SL));
return n;
}
Wie in vorherigen Kapiteln wird hier eine Klasse Complex mit ihren Methoden, wie multiply(), addC() und getLength() verwendet. Es handelt sich in der while-Schleife daher offensichtlich um die Iteration zNeu = zAlt2 + c, wobei c ein fester Punkt der komplexen Ebene ist.
Die Attribute SL und SW enthalten nach dem Verlassen der Schleife die Werte für die Strecken- bzw. Winkelsumme. Als ausgleichender Faktor wird hier 100 verwendet. Das Gesamtergebnis n besteht aus drei Summanden: der Anzahl der Schleifen bis zum Verlassen, der Streckensumme und der hundertfachen Winkelsumme.
Die Methode inversTangens(A,B) lässt sich unter Berücksichtigung der Winkel zwischen 0 und 2*PI so schreiben:
if(z>=0 && n<0) ergebnis = atan(z/n);
if(z<=0 && n <0) ergebnis = PI+atan(z/n);
if(z<=0 && n <0) ergebnis = PI+atan(z/n);
if(z>=0 && n <0) ergebnis = 2*PI+atan(z/n);
return ergebnis;
}
Der Unterschied im Ergebnis soll an drei Beispielen gezeigt werden. Das linke Bild zeigt jeweils das mit der Standardmethode gefärbte Bild. Rechts daneben die Färbung unter Einbeziehung von Winkel- und Streckensumme:
zNeu = ezAlt2 + c mit c = -0.02 + 0.06 * i :

zNeu = zAlt8 + c mit c = 0.7249999 + 0.0416665 * i :
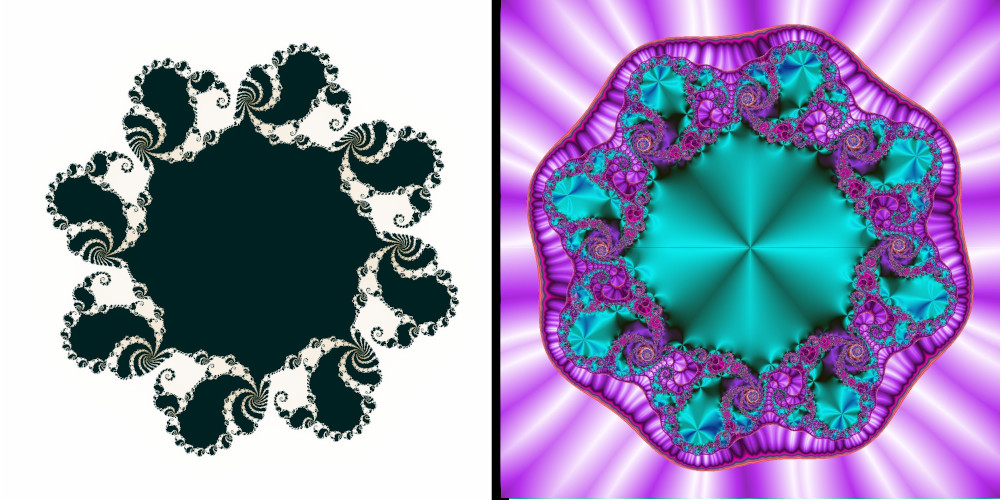
zNeu = zAltzAlt + c mit c = 0.90333342 + 0.4 * i :

Um ein Missverständnis zu vermeiden, sollte man festhalten, dass solch gravierende Unterschiede in der Qualität des Bildes besonders dann auftreten, wenn der Summand c für die Standardmethode ungünstig ist. Ungünstig bedeutet hier: die Anzahl der Iterationen bis zum Verlassen des Kreises unterscheiden sich nur wenig.
Die Farbunterschiede beinhalten nun nicht mehr nur die Geschwindigkeit mit der ein Kreis verlassen wird, sie sind viel mehr auch Indikator für die "Heftigkeit" der Bewegung bei der Iteration.
Feinschliff
Weniger schön ist, dass die Pixel aus dem Bereich der "Ordnung" recht eintönig
gefärbt sind. Ohne Strecken- und Winkelsumme wären die betreffenden Flächen gar einfarbig, da ja alle Werte dort nach der maximalen
Anzahl der Iterationen noch immer die Fluchtgrenze nicht ereicht haben. Verwenden wir als Beispiel die
Iteration zNeu = zAlt3 ⋅ sin(zAlt) + c .
Im Bild links im mittleren Bereich tut sich farblich wenig. ( Schwarze Kreise weisen auf Fixpunkte hin.)
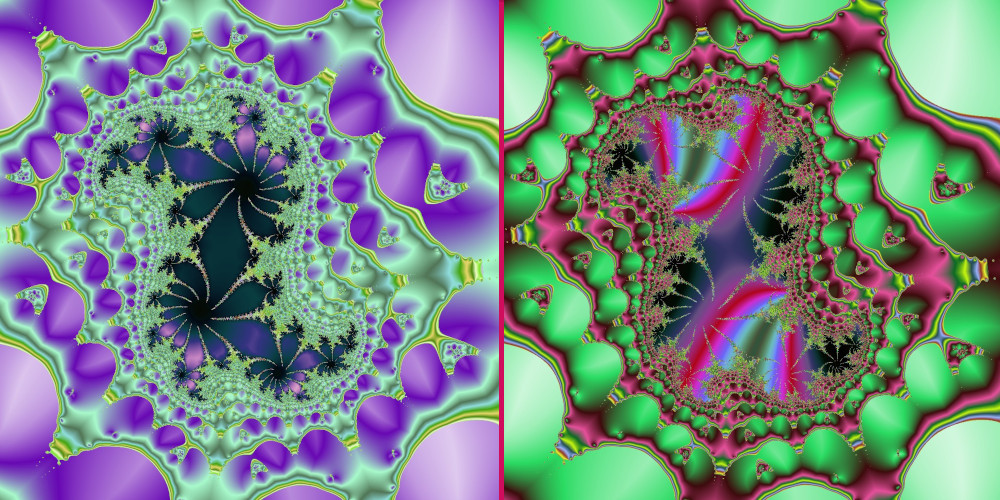
Wenn man in diesem Bereich als Färbekriterium aber den ersten Winkel bei der Iteration verwendet, dann bekommt man
deutlich größere Farbnuancen. Allerdings ist von eventuellen Fixpunkten nichts mehr zu sehen. (Bild oben rechts)
Ein weiteres Problem entsteht, wenn die Iteration die Entfernung vom Ursprung nicht korrekt testet, weil dieser NaN
(Not a Number) wird. In diesem Fall läuft die Iteration einfach weiter und wertet den Punkt als Ordnungspunkt.
Ein Beispiel: zNeu = tan(zAlt)3 + c

Wenn man die Iteration auf NaN testet und zum Beispiel den entsprechenden Punkten die Farbe weiß zuordnet, dann bekommt man die vielen
"weißen Blüten" wie im obigen Bild zu sehen. Prüft man dies nicht, dann fehlen diese Stellen.
"NaN" bedeutet, dass der errechnete Radius "unendlich" ist und die Schleife daher verlassen werden muss. Und dies
lässt sich durch fogenden Code testen:
Am sichersten ist es, wenn man diesen Test in allen Beispielen ausführt. Denn nicht immer erkennt man, ob NaN bei der Iteration vorkommt. Überraschenderweise kommt es bei der Iteration
zNeu = e zAlt3 + c zum Beispiel nicht vor:

Fallen (traps)
Man kann, wie Sie in den beiden letzten Kapiteln zum Thema "traps" gesehen haben, die Bilder dadurch etwas lebhafter
gestalten, in dem man Fallen einbaut. Hier wollen wir insgesamt neun davon verwenden. Den folgenden
Programmcode setzen Sie einfach an das Ende der while-Schleife ein. Die Reihenfolge bestimmt die Verdeckung: je
weiter oben im Code, desto weiter "oben" im Bild.
trapped = true;
int fWert = round(100*(float)laenge);
if (fWert > 255) fWert =255;
N =2*(o%8)*128+fWert;
break;
}
if(C1.subtractC(zNeu).getLength() kR){//Kreis mit Zentrum (1,1)
trapped = true;
double laenge11 =C1.subtractC(zNeu).getLength();
int fWert = round(100*(float)laenge11);
if (fWert > 255) fWert =255;
N =2*((o+1)%9)*128+fWert;
break;
}
if(C2.subtractC(zNeu).getLength() kR){//Kreis mit Zentrum (-1,1)
trapped = true;
double laenge11 =C2.subtractC(zNeu).getLength();
int fWert = round(100*(float)laenge11);
if (fWert > 255) fWert =255;
N =2*((o+2)%9)*128+fWert;
break;
} if(C3.subtractC(zNeu).getLength() kR){//Kreis mit Zentrum (-1,-1)
trapped = true;
double laenge11 =C3.subtractC(zNeu).getLength();
int fWert = round(100*(float)laenge11);
if (fWert > 255) fWert =255;
N =2*((o+3)%9)*128+fWert;
break;
} if(C4.subtractC(zNeu).getLength() kR){//Kreis mit Zentrum (-1,-1)
trapped = true;
double laenge11 =C4.subtractC(zNeu).getLength();
int fWert = round(100*(float)laenge11);
if (fWert > 255) fWert =255;
N =2*((o+4)%9)*128+fWert;
break;
}
if( zNeu.im 1+dy && zNeu.im > 1-dy ){//Gerade auf Höhe y = 1
trapped = true;
int fWert = round(1000*abs(B-1));
if (fWert > 255) fWert =255;
N =2*((o+5)%9)*128+fWert;
break;
}
if( zNeu.im -1+dy && zNeu.im > -1-dy ){//Gerade auf Höhe y = -1
trapped = true;
int fWert = round(1000*abs(B-1));
if (fWert > 255) fWert =255;
N =2*((o+6)%9)*128+fWert;
break;
}
if( zNeu.re 1+dx && zNeu.re > 1-dx ){//Gerade bei x = 1
trapped = true;
int fWert = round(1000*abs(A-1));
if (fWert > 255) fWert =255;
N =2*((o+7)%9)*128+fWert;
break;
}
if( zNeu.re -1+dx && zNeu.re > -1-dx ){//Gerade bei x = -1
trapped = true;
int fWert = round(1000*abs(A-1)); if (fWert > 255) fWert =255;
N =2*((o+8)%9)*128+fWert;
break;
}
zNeu = zAlt2 + c

zNeu = zAlt4 + c
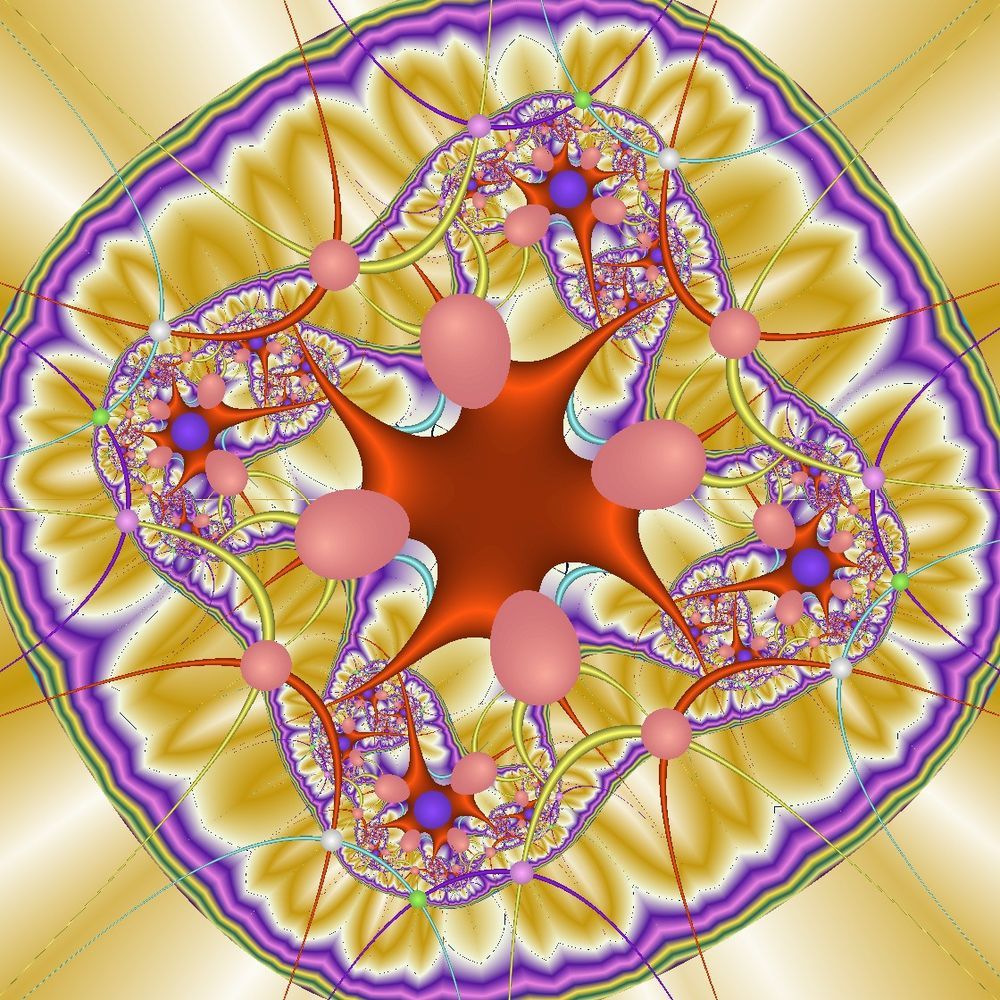
zNeu = zAlt8 + c

zNeu = zAlt5 + c

zNeu = zAlt5 + zAlt2 +c
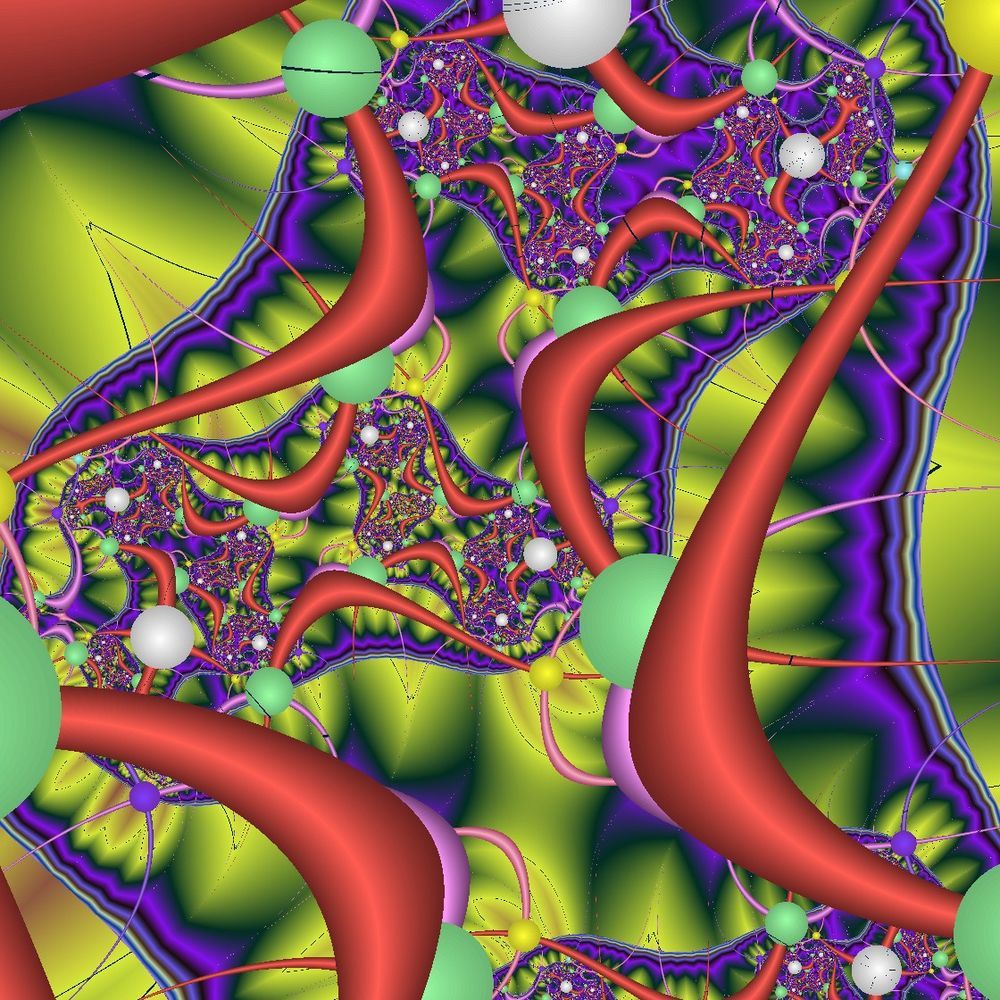
zNeu = zAlt2 + sin(zAlt) + c

zNeu = zAltzAlt + c

zNeu = ezAlt2 + c
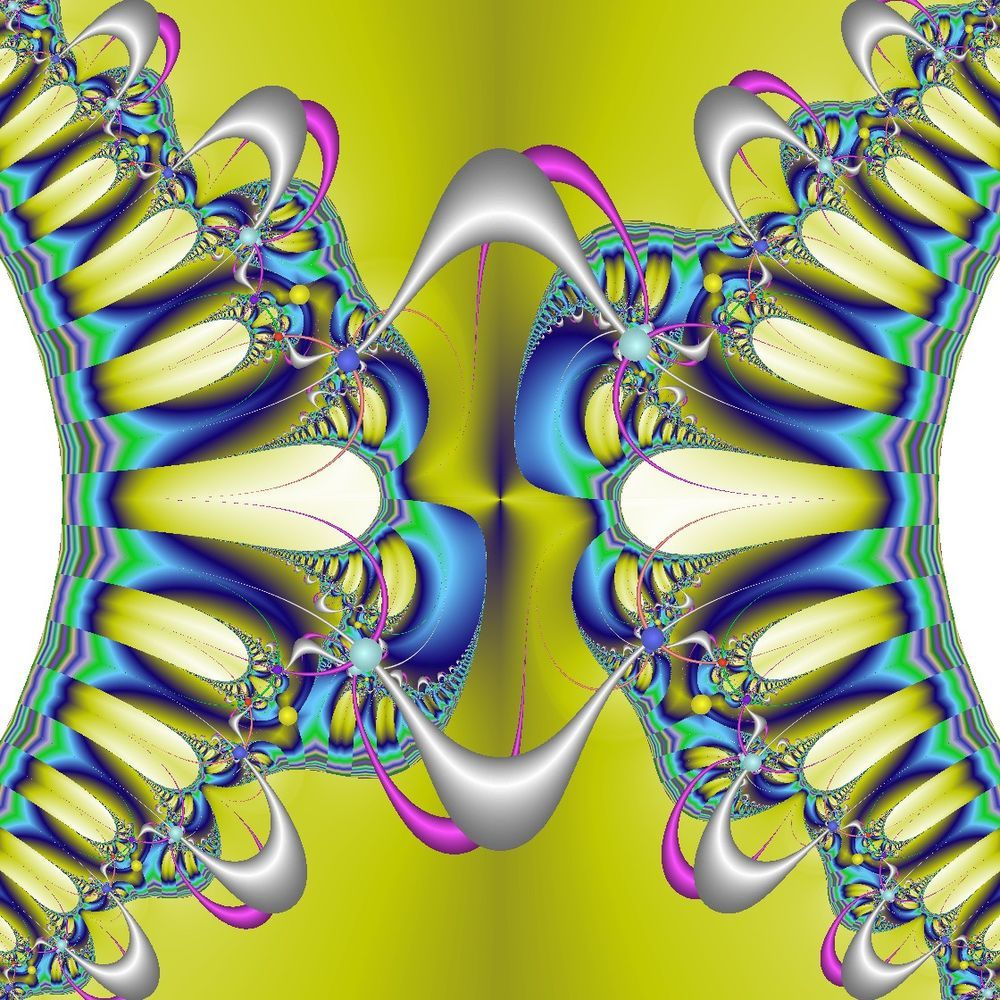
Beachten Sie bei den folgenden Sketchen, dass die Anzahl der Threads mit
anzahlThreads = Runtime.getRuntime().availableProcessors()-4;
ausgelesen wird. Dies müssen Sie an die Anzahl der Core in ihrem Prozessor anpassen.
Julia Fraktale mit üblicher Färbung
Julia Fraktale mit spezieller Färbung
Julia Fraktale mit spezieller Färbung und Traps
Menu