Menu

Fraktale: Julia- und Fatou-Mengen

Julia quadratisch: z_neu = z_alt²+c

Im letzten Kapitel haben wir mit Hilfe der "Mandelbrotmenge" einen c-Wert ausgesucht und mit diesem Wert eine gefüllte "Julia-Menge" gezeichnet. Die Anführungszeichen sind gesetzt, weil die beiden Mengen nur anschaulich und dazu noch recht willkürlich festgelegt wurden. Im Prinzip ging es immer darum, ob ein Orbit bei vorgegebener Iterationstiefe eine Schranke reißt oder nicht. Zumindest im Fall der Julia-Menge wollen wir das nun etwas besser machen, ohne gleich mit unverständlichen Formeln um uns zu werfen...
Die für die Julia-Mengen zugelassenen Iterationen sind gebrochen-rationale Funktionen auf der Menge der komplexen Zahlen. Wir betrachten zunächst die einfachste nicht-lineare Iteration: z_neu = z_alt² (c = 0).
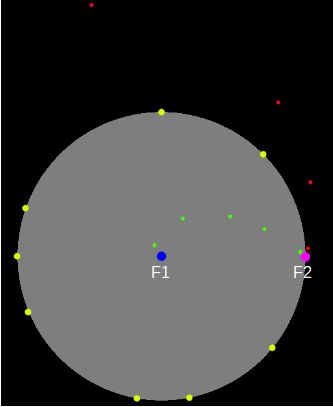
Es gibt offensichtlich zwei Fixpunkte: F₁ = 0 und F₂ = 1. Wir lassen uns einige Orbit-Punkte anzeigen. Die gelben Punkte sind bei F₂ gestartet, die grünen links daneben (also innen) und die roten rechts daneben (also außen). Startwerte z₀ innerhalb des Einheitskreises führen offensichtlich schnell zum anziehenden Fixpunkt F₁. Diejenigen, die außerhalb liegen, führen zum (ebenfalls anziehenden) Fixpunkt ∞ (unendlich). Die Punkte auf dem Einheitskreis aber bleiben immer auf der Kreislinie. Diese trennt den "Gefangenenbereich" (grau) vom "Fluchtbereich" (schwarz) und wird Julia-Menge genannt. Das Komplement in ℂ ∪{ ∞} der Julia-Menge heißt Fatou-Menge(grau und schwarz). Die Julia-Menge selbst ist "abstoßend", denn Punkte in ihrer Nähe werden entweder zu F₁ oder Richtung unendlich gezogen. (Im nachfolgenden interaktiven Sketch können Sie das selbst genauer untersuchen. Der Wert c = 0 ist dort bereits durch einen gelben Punkt markiert. )

Um eine Julia-Menge zeichnen zu könnte, muss man noch folgendes wissen:
Julia-Mengen sind bezüglich der Iteration und ihrer Umkehrung invariant. Das bedeutet, wenn ein Punkt auf der Julia-Menge liegt, dann ist sein Bild- und Ursprungs-Punkt ebenfalls auf der Julia-Menge.
Da die Julia-Menge außerdem abstoßend ist, muss die Umkehrung der Iteration anziehend sein. Das darauf beruhende Verfahren nennt man "inverse Iterations-Methode (IIM)". Die inverse Iteration ist in diesem Fall:
Nun ist diese Iteration wegen der beiden Möglichkeiten (+/-) nicht eindeutig. Abhilfe schafft die Regel, den Zufall bestimmen zu lassen, welches Vorzeichen gewählt werden soll.

Links ein Ausschnitt einer gefüllten Julia-Menge. Die gelben Punkte wurden mit dem IIM-Verfahren erzeugt. Kaum zu glauben: Eine Million mal wurde die inverse Iteration ausgeführt und dennoch "fehlt" ein großer Teil der Julia-Menge! Eine erste Idee wäre, dass man die Anzahl der inversen Iterationen erhöht oder den Algorithmus mehrfach startet. Der Weg durch den (+/-)-Entscheidungsbaum dürfte schon nach wenigen Iterationen ein anderer als der vorherige sein (2^1000000 verschiedene Wege...).
Eine zweite Idee bezieht sich auf den (+/-)-Entscheidungsbaum: Man notiert bei jedem Ergebnis, welches Pixel getroffen wird. Ist ein Pixel beispielsweise n mal getroffen und führt die nächste Entscheidung wieder zum gleichen Pixel, wählt man den anderen Weg. Kommt man aber an eine Stelle des Baums, bei dem beide Pixel schon n mal getroffen wurden, startet man mit einem beliebigen Punkt von vorn. Da die inverse Iteration bezüglich der Julia-Menge anziehend ist, muss man lediglich zum Beispiel die ersten hundert Punkte (wie beim Feigenbaum-Diagramm) unbeachtet lassen. Dieses Verfahren heißt "Modifizierte inverse Iterations-Methode", kurz MIIM .
Das Bild oben rechts wurde durch hundert-malige Anwendung des IIM-Verfahrens mit je einer Million inverser Iterationen und außerdem durch ebenfalls hundert-maliges anwenden des MIIM-Verfahrens erzeugt. Wir können daraus schließen, dass das Treffen mancher Punkte der Julia-Menge mit IIM und MIIM extrem unwahrscheinlich ist. Das ist allerdings nicht immer so, wie sie an fogendem Bild sehen können. Hier wurde IIM nur einmal angewendet:


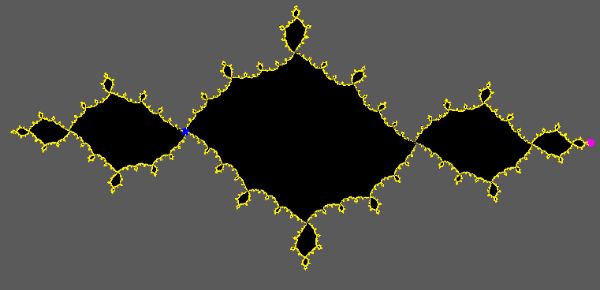
Im folgenden Sketch können Sie nun selbst überprüfen, was IIM und MIIM taugen...

Falls die Mandelbrotmenge angezeigt wird:

Falls die Juliamenge angezeigt wird:


In beiden Situationen:


Die Menge der Möglichkeiten ist zunächst verwirrend. Daher finden Sie hier ein Vorschlag, wie man vorgehen kann. Drücken Sie der Reihen nach folgenden Tasten: P,V,V,V,J,f,O,i,j
Dann landen Sie eventuell bei einem ähnlichen Bild:



(Hier kann der obige Sketch auch runtergeladen werden!)

Um zu demonstrieren, dass mit IIM und MIIM bei manchen c-Werten ein großer Teil der Julia-Menge fehlt, ließen wir die gefüllte Julia-Menge mit anzeigen. Mit bloßem Auge kann man so die korrekte Julia-Menge erahnen. Die "Boundary Scanning-Methode" (BSM) nutzt nun die leicht zu zeichnende gefüllte Julia-Menge, um die Julia-Menge zu zeichnen. Im folgenden Bild wird die Idee erklärt:


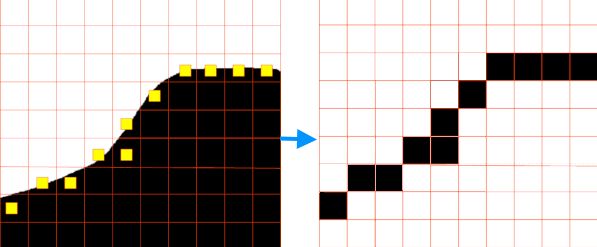
Das Bild der gefüllten Julia-Menge wird von einem Netz aus Quadraten überzogen. Die Seitenlänge der Quadrate sollte möglichst klein sein. Am besten verwendet man als Quadrat ein Pixel. Nun wird an allen vier Eckpunkten die Julia-Iteraton bis zur Iterationsgrenze n durchgeführt. Für jedes Pixel zählt man die Anzahl der Ecken, für die Iteration Konvergenz vermuten lässt. Ist diese Anzahl gleich 2 oder 3, wird das Pixel der Julia-Menge zugeordnet. Das folgende Bild zeigt den Unterschied mit einem c-Wert, das einen Attraktor der Periode 37 in der Julia-Menge erzeugt. Oben die BS- und unten die II-Methode.


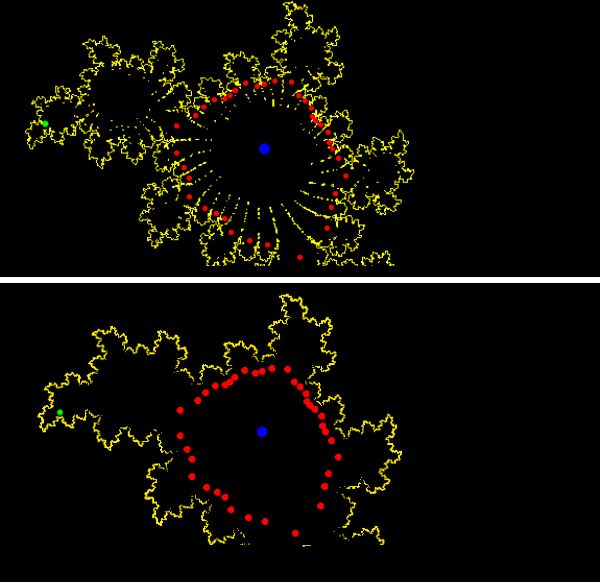
Der zugehörige Sketch Mandelbrot-Julia-BSM wurde multithreaded ausgeführt. Zusätzlich ist der BS-Algorithmus sehr viel schneller als die II-Methode. Von daher erstaunt es nicht, dass das Zeichnen einer Julia-Menge mittels BSM nur wenige Sekunden benötigt.

Die BS-Methode benötigt eine ausgefüllte Julia-Menge. Das übliche Verfahren hierbei ist die Flucht-Methode : Man legt zunächst eine maximale Iterationsgrenze iMax und eine obere Schranke S fest. Wird bei Iteration bis iMax die obere Schranke S nicht übertroffen, wird das entsprechende Pixel beispielsweise schwarz gezeichnet. Wird iMax übertroffen, so wird das Pixel weiß eingezeichnet. Auf das so gewonnene schwarz-weiß Bild wird die BSM angewendet.
Häufig wird die Flucht-Methode durch die EDEM (external distance estimation method) ersetzt. Einzelheit zu dieser Methode findet man zum Beispiel hier in den Wikibooks. Das Bild links ist mit dem oben erwähnten Sketch Mandelbrot-Julia-BSM erstellt worden. Nach einem Rechtsklick, um das Fenster zu aktivieren, muss man dort die Taste 'd' drücken, um die EDEM anzuwenden. Die Julia-Menge wird zur Unterscheidung weiß eingetragen.

Julia allgemein

Im Abschnitt oben wurde die bekannteste Art der Julia-Menge mit der Iterations-Formel
z_neu = z_alt²+c untersucht. Diese Einschränkung war zunächst berechtigt, weil schon in dieser einfachen Form grundlegende Erkenntnisse über Julia-Mengen entdeckt werden konnten.
Allgemein werden Julia-Mengen jedoch über die viel weiter gefasste Iterations-Formel 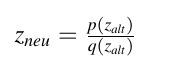definiert. p und q sind hierbei ganzrationale Funktionen über der Menge der komplexen Zahlen. Der "Grad" dieser Iteration soll hierbei der maximale Grad von p und q sein.
Zwei Eigenschaften von Julia-Mengen sollen hier (ohne Beweis) genannt werden:
Julia-Mengen haben keine inneren Punkte.
Für uns heißt das insbesondere, dass Julia-Mengen "unendlich dünn" sind, dass also alle Bilder von ihnen nur den Ort zeigen, an denen sie ungefähr zu finden sind.
Stellen Sie sich nun eine beliebig kleine Umgebung einer Julia-Menge U vor.
Es gibt dann eine natürliche Zahl k, sodass J = f^k (U)
In einfachen Worten ausgedrückt: Wenn man auf diese kleine Umgebung U die Iteration f k mal anwendet, erhält man wieder die ganze Julia-Menge J. Das bedeutet, dass alle Informationen über die Julia-Menge in jeder noch so kleinen Umgebung der Menge bereits enthalten sind.

Wir interessieren uns im Folgenden hauptsächlich für Julia-Iterationen, die aus der Newtonschen Methode der Nullstellenbestimmung einer Funktion f entstehen. Ein einfaches Beispiel soll das Vorgehen erläutern. Die Funktion f, auf der wir die Newton-Iteration aufbauen, nennen wir hier Grundfunktion. Als Beispiel dient uns hier die Funktion f, gegeben durch :f(z) = z² + c. Die beiden Nullstellen dieser Funktion sind √-c und -√-c. Die Nullstellen dieser Grundfunktion bestimmt man näherungsweise mit dem Newton-Verfahren. Die allgemeine Iterationsformel des Newtonverfahrens ist: 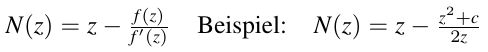Nun "vergessen" wir die ursprünglich Iteration f und widmen uns nur noch der Newton-Iteration N. Die Nullstellen von f werden nun zu den Fixpunkten und Attraktoren von N. Wenn es mehrere Attraktoren gibt, dann muss es disjunkte Bereiche in ℂ geben, die zu den verschiedenen Attraktoren führen.

Die Fixpunkte von N (Nullstellen von f) kann man durch die newtonsche Iteration N ganz leicht näherungsweise ausrechnen. Das Verfahren konvergiert sehr schnell, so dass man meist nur wenige Iteratiosschritte durchführen muss. Wenn der Grad von N beispielsweise fünf ist, dann kann man zunächst versuchen fünf verschiedene Fixpunkte in eine ArrayList einzutragen. Das klappt auch gut, solange es keine mehrfachen Nullstellen von f gibt. Andernfalls sucht man nur nach vier verschiedenen Nullstellen und so weiter. Der Algorithmus ist demnach:

Eine zufällige komplexe Zahl z₀ im Bildbereich wählen. Maximal n Iterationen N mit dieser Zahl durchführen. Sobald der Abstand zwischen z_n und z_n-1 kleiner als eine vorgegebene Zahl ε ist, z_n in die Fixpunkte-Liste eintragen.
Hat man alle Fixpunkte gefunden, ordnet man jedem eine Farbe zu. (Zum Beispiel im HSB-Farbsystem dem Realteil den Farbton und dem Imaginärteil die Helligkeit). Dann prüft man bei jedem Pixel zu welchem Attraktor (= Fixpunkt) der zugehörige Wert z₀ konvergiert und färbt ihn mit der zugehörigen Farbe des Attraktors ein. Verwendet man das obige Beispiel, dann ist das Ergebnis entäuschend:


Ändert man c, dann ändert sich die Steigung der Geraden. Und es ist genau diese Gerade, die die Julia-Menge repräsentiert. Würde ein Startpunkt exakt auf der Julia-Menge liegen, dann wird der Bildpunkt, wie wir oben gesehen haben, wieder auf der Julia-Menge landen.
Ein ganz anderes Ergebnis bekommt man, wenn man als grundliegende Funktion f mit f(z) = z³ + c wählt.



Die drei Fixpunkte sind im Bild links weiß eingetragen. Rechts daneben wurden in einer Variation des BSM-Verfahrens alle Pixel weiß eingetragen, für die höchstens zwei Ecken des Quadrats zum gleichen Fixpunkt führen. Alle anderen Pixel färbt man schwarz. Auf diese Weise bekommt man eine Vorstellung der (eigentlich unendlich dünnen) Julia-Menge.
Es gibt hier offensichtlich drei disjunkte Gebiete, die als Einzugsgebiete der jeweiligen Fixpunkte definiert wurden. Entsprechend nennt man sie auch Fatou-Gebiete. Man kann zeigen, dass die Julia-Menge Rand jedes Fatou-Gebiets ist. Hat man aber mindestens drei Fatou-Gebiete, dann ist dies, wie man leicht sieht, nur dann möglich, wenn die Julia-Menge fraktal ist.
Unten können Sie verschiedene "Newton-Julia" Sketche runterladen und testen. An der Bezeichnung kann man erkennen, was der Sketch tut: Die erste Zahl nennt die Anzahl der Nullstellen, die zweite Zahl den Grad der Grundfunktion f. Ein angehängter Buchstabe "a" zeigt an, dass nicht nur Potenzen von n und 0 in z vorkommen. Die Grundfunktion f ist zum Beispiel gegeben durch f(z) = z⁷ + 4z³ + c. Beim Sketch "Newton-Julia7_7" hingegen ist die Funktion f gegeben durch f(z) = z⁷ + c.
(Man kann sich bei allen Sketchen die Lokalisierung der Julia-Menge in das Bild mit den farbigen Fatou-Gebieten mit Taste eintragen lassen. Leider werden dabei die Fatou-Gebiete stark in Mitleidenschaft gezogen. Daher sind die Repräsentationen der Julia-Mengen im folgenden Bild zusätzlich auf schwarzen Hintergrund gezeichnet. Die weißen Einzelpunkte zeigen die Fixpunkt/Attraktoren von N.)



Wie bestimmt man die Attraktoren? Mit der puren Rechenkraft der Computer! Schauen wir uns die beiden Bilder oben an. Der Grad von N ist hier 11, also versucht man zunächst auch 11 Fixpunkte zu finden. Man wählt einen zufälligen Startwert aus und iteriert so lange, bis der Abstand zwischen letztem und vorletztem iterierten Wert kleiner als zum Beipiel 0,0000000001 ist. Sofern er nicht schon vorhanden ist, trägt man jeden neu gefundenen Fixpunkt in eine ArrayList ein. Kommen keine 11 Fixpunkte zusammen, so merkt man das daran, dass die Suche zu keinem Ende kommt. Dann versucht man es zunächst mit 10 Fixpunkten. In unserem Beispiel erhält man nach wenigen Sekunden:



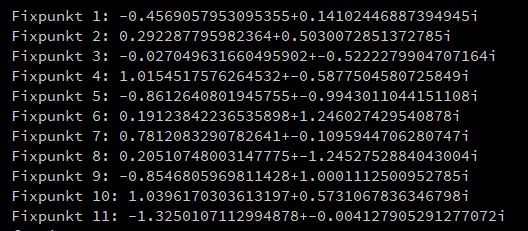
Die Newton-Julia-Sketche unten lassen noch weitere Bildinterpretationen zu. Das folgende Bild zeigt die Anwendung eines "Trap-Algorithmus" (hier besteht die "Falle" aus neun Kreisen). Diese Methode wird in einem extra Kapitel behandelt werden.



Eine weitere Interpretation zeigt das folgende "Konvergenzbild". Je mehr Iterationen bei einem Punkt nötig sind, den zugehörigen Attaktor bis auf eine vorgegebene Genauigkeit zu erreichen, desto heller wird der Punkt eingefärbt. Auf diese Weise wird der Ort der Julia-Menge deutlich sichtbar.





Mandelbrot-Julia-IIM   Mandelbrot-Julia-BSM.

Newton-Julia 2_2   Newton-Julia 3_2   Newton-Julia 3_3

Newton-Julia 3_4   Newton-Julia 5_5   Newton-Julia 7_7

Newton-Julia 7_7a   Newton-Julia 11_11   Newton-Julia 11_11a

Menu