Kryptologie

Cat-Map-Perm

Wenn Sie sich das Kapitel Maps durchgelesen haben, wissen Sie, dass Transformations-Matrizen, deren Determinante den Betrag 1 haben, eine Periode P besitzen. Mit anderen Worten: Wenn man eine derartige Abbildung P mal (modulo Bildbreite - die Punkte müssen ja im Bild bleiben) durchführt, kommt wieder das alte Bild zum Vorschein. Nehmen wir an, die Periode sei 150. Wenn man das Bild zum Beispiel 100 mal abbildet, kann man außer merkwürdigen Farbmustern nichts erkennen. Bildet man dieses Bild mit der gleichen Matrix weitere 50 mal ab, erhält man das ursprüngliche Bild. Verwendet man als mögliche Matrizen diejenige Teilmenge, die sich mit zwei natürlichen Zahlen x und y, mit x,y < 600 schreiben lassen, erhält man 360 000 verschiedene Matrizen. Das ist zwar nicht wenig, für eine ernsthafte Verschlüsselung aber taugt dieses Verfahren nicht.

Ganz anders sieht die Sache aus, wenn man das Ergebnis der ersten (vielfachen) Arnold-Transformation (= AT) erneut abbildet. Dieses mal aber mit einer anderen Matrix. Dann gäbe es schon 130 Milliarden verschieden Kombinationen. Wenn man nun davon ausgeht, dass jede AT im Schnitt 10 mal angewandt wird, sind wir bei 13 Billionen Möglichkeiten. Damit begnügen wir uns nicht. Was genau unser Programm leisen soll, können Sie dem folgenden Bild entnehmen:

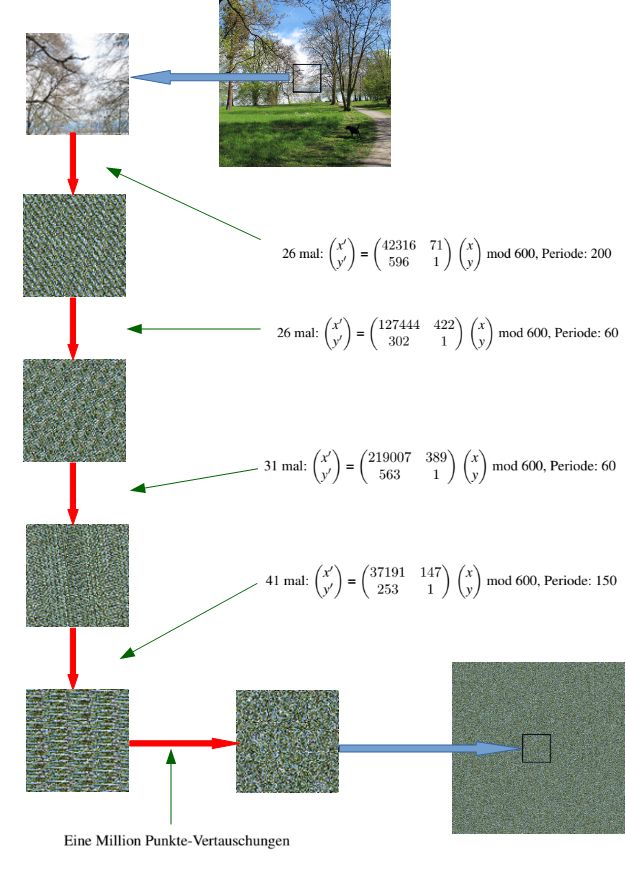
Es werden vier verschiedene ATs angewandt. Im ersten Beispiel hat das Programm drei Pseude-Zufallszahlen zwischen 0 und 599 errechnet: 71, 596 und 426. Die ersten beiden Zahlen benötigt man zur Bestimmung der Transformationsmatrix, die dritte Zahl gibt an, wie oft diese Transformation durchzuführen ist. Die durch die beiden ersten Zahlen eindeutig bestimmte Matrix hat aber die Periode 200. Somit muss man die Abbildung nicht 426 mal durchführen. Es genügen 26 mal. Die zugehörige inverse Abbildung hat die gleiche Matrix. Man muss die Abbildung aber nun 200-26 = 174 mal anwenden, um zum Originalbild zurückzukehren.

Natürlich ist es nicht sonderlich sinnvoll, ein Landschaftsfoto zu verschlüsseln. Wir haben es statt eines Geheimtext-Bildes nur deshalb gewählt, weil man hier besser beobachten kann, was in den einzelnen Schritten passiert. Sie können so in den vergrößerten Bildauschnitten sehen, dass auch das selbst das letzte Ergebnis der ATs noch immer ein gewisses Muster aufweist. Zur Sicherheit werden wir daher zum Schluss eine Million Permutationen der Bildpunkte vornehmen. Wenn die ersten vier Pseudo-Zufallszahlen des Permutationsschlüssels zum Beispiel aus den Zahlen 387, 211, 589 und 94 bestehen, dann soll die Farbe des Pixels (387,211) mit der Farbe des Pixels (589,94) vertauscht werden. Und wie Sie sehen, kann man im Ergebnisbild kein Muster mehr erkennen. Eine derartige Permutation lässt sich übrigens sehr einfach rückgängig machen: Man führt alle Permutationen in umgekehrter Reihenfolge aus.

Aber wie bereits geschrieben geht es uns hier darum, Text zu verschlüsseln. Dieser Text soll nur aus zwei verschiedenen Pixelfarben bestehen: schwarz (0) und weiß 255). Denn eine solch chaotische Verteilung der schwarzen Punkte, wie im Bild unten links, lässt sich hervorragend in einem Foto verstecken. Dazu im nächsten Kapitel mehr...

Weshalb ist die Hintereinander-Ausführung zweier verschiedener ATs ungleich schwerer rückgängig zu machen, als die zweier gleicher ATs? Probieren Sie es aus: Wenn Sie zwei verschieden AT-Matrizen miteinander multiplizieren, dann können Sie die doppelte Transformation auch mit dieser einen durchführen. Allerdings ist die Determinante der Matrix, die aus dem Produkt entstanden ist wegen der Modulo N Rechnung in der Regel nicht mehr vom Betrag 1. Und somit gibt es auch keine Periode mehr. Da die Berechnung der Perioden der ATs viel Rechenaufwand verlangt, ist sie als Multi-Thread angelegt.

Für eine wirklich sichere Verschlüsselung darf man freilich keine Pseudo-Zufallszahlen verwenden. Der Sketch verwendet daher SecureRandom(). Hierbei werden aus dem Betriebssystem im Prinzip unvorhersagbare Zahlen entnommen, mit deren Hilfe die nächste Zufallszahl errechnet wird. Interessant: Bildbreiten, die prim sind, ergeben im Allgemeinen eine höher Periode.

Sketch Verschlüsselung mit Arnold-Transformation und Permutation.

<Menu