Maps
Anosovs Katzenabbildung
Unter einer map versteht man in der Mathematik eine Funktion (Regel), die die Veränderung der Lage von Punkte beschreibt. Man kann diese Funktion beliebig oft ausführen. In vielen Fällen entsteht dann ein Fraktal. Ein einfaches Beispiel: Stellen Sie sich ein Pixelbild vor. Jedem Pixel auf der Fläche wird durch die Funktion ein neuer Ort zugewiesen. Das Ergebnisbild ist möglicherweise dann völlig anders, - erst recht, wenn man die Funktion mehrfach anwendet.
Anosovs "Katzenabbildung", auch Arnold-Transformation (AT) genannt, ist eine Abbildung, mit der man beispielsweise ein quadratisches Digitalbild so abbilden kann, dass einerseits keine Information verloren geht, und andererseits bereits nach wenigen Transformationen nur noch Chaos im Bild zu sehen ist. Und so ist die AT definiert (N ist die Bildbreite in Pixel des quadratischen Bildes):
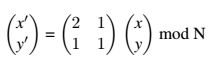
x' = (2x + y) mod N
y' = ( x + y) mod N
Im unten ablaufenden Sketch sehen Sie, wie sich ein Bild (N=377) nach jeder AT verändert.
Und was besonders erstaunlich ist: Nach 14 Transformationen erhält man wieder das originale Bild. Kurz formuliert:
Die Periode der AT mit N = 377 ist P = 14. Der Zusammenhang von N und P ist, wie wir später sehen werden, alles
andere als einfach...
Die obige Matrix ist sehr speziell. Als Wert für die Determinante erhält man D = 2 ⋅ 1 - 1 ⋅ 1 = 1. Tatsächlich führen alle Matrizen mit D = ± 1 zu einer Periode der Transformation.
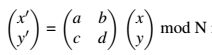
mit |ad - bc| = 1
Eine häufig genutzte Teilmenge ist:
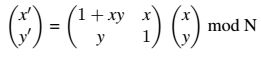
mit x,y ∈ {0,1,2,...N-1}. Bereits diese Teilmenge liefert für 400 Pixel breite Bilder 160 000 verschiedene Abbildungen!
Vielleicht werden Sie sich fragen, worin der Nutzen einer derartigen Map besteht. Es gibt mehr Anwendunsmöglichkeiten
als Sie denken! Wir jedenfalls werden die AT sowohl in der Abteilung Kryptologie als auch in
Steganographie verwenden.
Wir werden dann allerdings die Information benötigen, wie die Periode P von der Bildbreite N und von der
Transformationsmatrix abhängt. Ein entsprechender Sketch liefert die gewünschten Informationen. Hier ein
Beispiel:
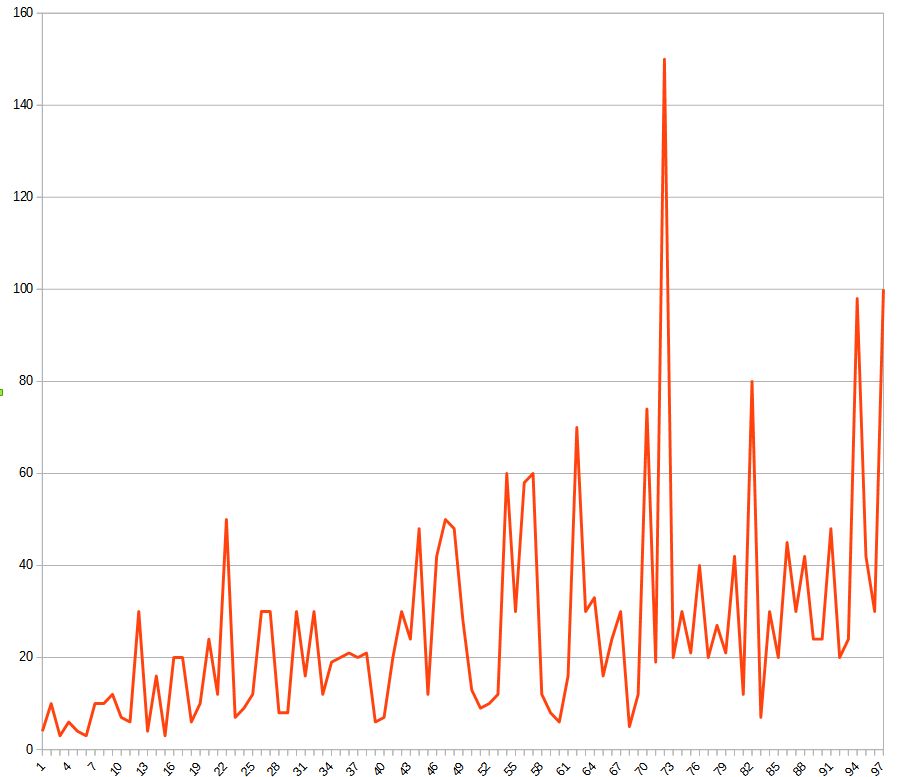
Die x-Achse zeigt die Bildbreite N und die y-Achse die Periode P an. Als Matrix wurde die ursprünglich von
Anosovs vorgeschlagen Matrix (siehe oben)verwendet.
Sketch Periode-Bestimmung.
Menu