Simulation
Mathematisches Pendel
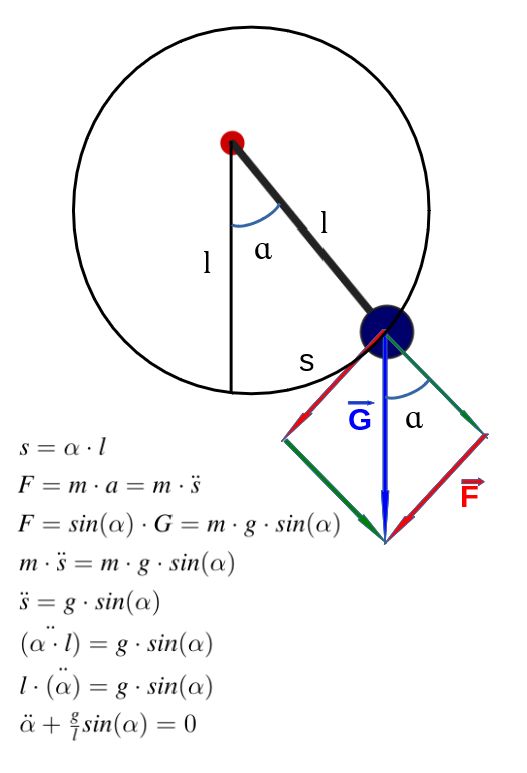
Im Kapitel "Physikalische Simulationen" unserem Buch wird das mathematische Pendel bereits behandelt. Allerdings gibt es dort eine wesentliche Einschränkung: Die Auslenkungswinkel des Pendels sollten in jedem Fall kleiner als 10 ° sein. Sobald man diese Einschränkung fallen lässt, gibt es keine durchgehend definierte Lösungsfunktion. Wie Sie oben links in der Herleitung der Differenzialgleichung sehen, bleibt die Sinusfunktion am Schluss stehen. Wenn man große Winkel zulassen will, muss man daher mit numerischen Näherungsverfahren arbeiten. Es gibt nicht wenige, immerhin. Allerdings sollte bei einer sinnvollen Näherung die Gesamtenergie konstant bleiben. Eine Möglichkeit, dies zu erreichen, ist die Verwendung der "Symplectic Euler"-Methode.
Wenn mit wn der Winkel in der n-ten Iteration bezeichnet wird und mit
gn die Winkelgeschwindigkeit in diesem Moment, dann bekommt man die folgenden Werte,
nachdem Δt verstrichen ist, durch diese Iterationen:
wn+1 = wn + Δt · gn
gn+1 = gn - Δt · K · sin(wn+1)
Weitere Informationen zum Thema
"mathematisches Pendel" finden Sie bei Wikipedia.
Im Kapitel "Physikalische Simulationen" in unserem Buch wird das mathematische Pendel bereits behandelt. Allerdings gibt es dort eine wesentliche Einschränkung: Die Auslenkungswinkel des Pendels sollten in jedem Fall kleiner als 10 ° sein. Sobald man diese Einschränkung fallen lässt, gibt es keine durchgehend definierte Lösungsfunktion. Wie Sie links in der Herleitung der Differenzialgleichung sehen, bleibt die Sinusfunktion am Schluss stehen. Wenn man große Winkel zulassen will, muss man daher mit numerischen Näherungsverfahren arbeiten. Es gibt nicht wenige, immerhin. Allerdings sollte bei einer sinnvollen Näherung die Gesamtenergie konstant bleiben. Eine Möglichkeit, dies zu erreichen, ist die Verwendung der "Symplectic Euler"-Methode.

Wenn Sie mehrfach in die Animation des Pendels geklickt haben, bekommen Sie ein ähnliches Bild wie links. Dabei erkennt man, dass es grundsätzlich zwei Arten von Trajektorien gibt: Geschlossene und ungeschlossene Linien. Die geschlossenen Linien gehören zu Pendelbewegungen, die tatsächlich hin- und herschwingen. Die anderen gehören zu Pendeln, die sich überschlagen. Die rote Linie ist die sogenannte "Seperatix". Sie trennt die beiden Bereiche voneinander. Natürlich gibt es diese Bewegung nicht wirklich, denn sie müsste im obersten Punkt stehenbleiben, aber auch gleichzeitig alle anderen Phasenpunkte erreichen.
Nun untersuchen wir, was sich ändert, wenn wir Reibung zulassen. Wie sieht das zughörige Phasendiagramm aus? Es ändert sich eigentlich nicht viel:
wn+1 = wn + Δt · gn
gn+1 = gn - Δt · K · sin(wn+1) - Δt · A · gn
Die Reibungskonstante A ist proportional zur Winkelgeschwindigkeit und reduziert diese mit der Zeit. Ebenfalls noch wichtig: Je kleiner Δt desto genauer die Simulation. Hier die Interation nach Euler:
w0 = V.x; g0 = V.y;
for(int i =0; i< N;i++){
x1 = w0 +g0*Delta;
y1 = g0 -(A*g0+B*sin(w0))*Delta;
kw = round(map(x1,MinX,MaxX,0,width));
kg = round(map(y1,MaxY,MinY,0,height));
point(kw,kg);
w0 = x1; g0 = y1;
}
}
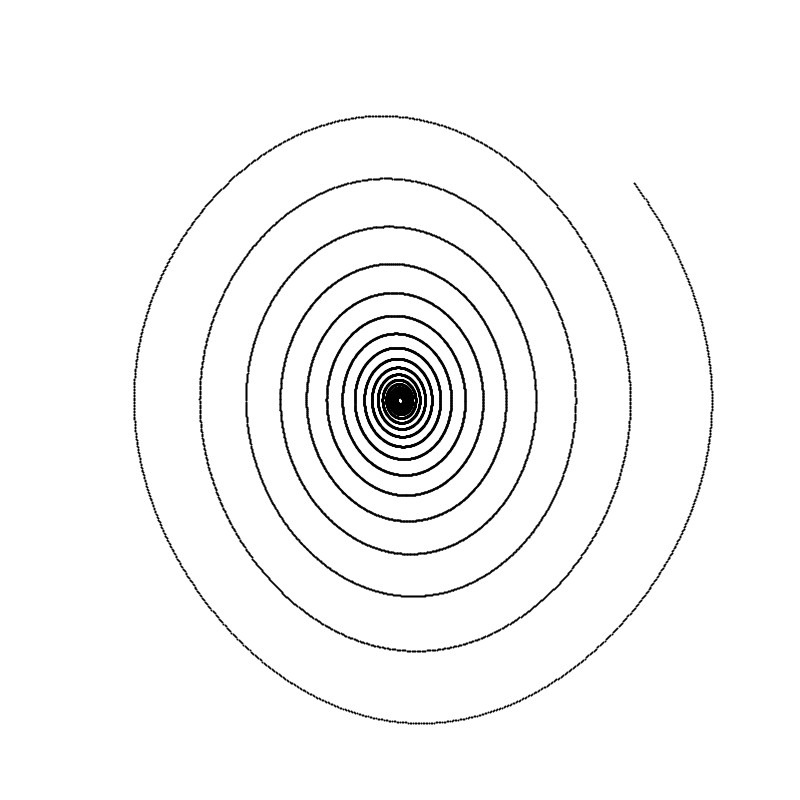
Δt = 0.02 zeigt bereits deutlich die Abstände der Punkte:
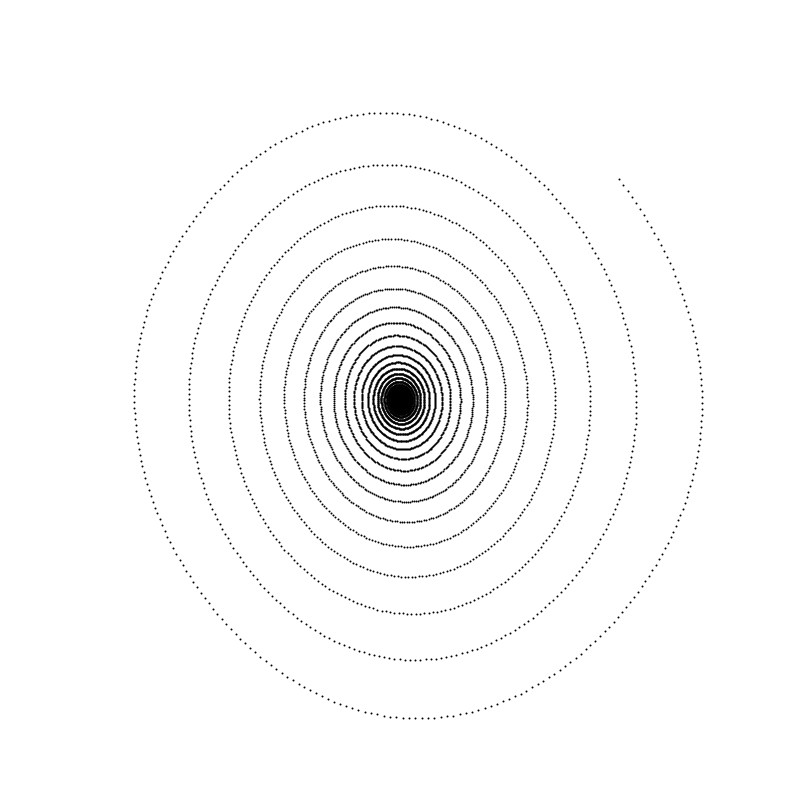
Klar ist, dass kleinere Δt die reale Situation besser simulieren, als größere. Das ist sicher richtig. Aber schauen Sie sich nun das Bild für Δt = 0.10 an:

Hier bekommt die Trajektorie eine Art "Wellenbildung". Das könnte ein Hinweis auf eine neu Art Periodizität hindeuten. Wenn wir in das Bild zoomen, kann man diese Wellen deutlicher sehen:

Man kann die Vergrößerung von Δt nicht beliebig lang betreiben. Oberhalb von Δt =1.8 verschwindet die Trajektorie Richtung unendlich große Geschwindigkeit. Aber falls Δt =1.8 entsteht folgender Attraktor:
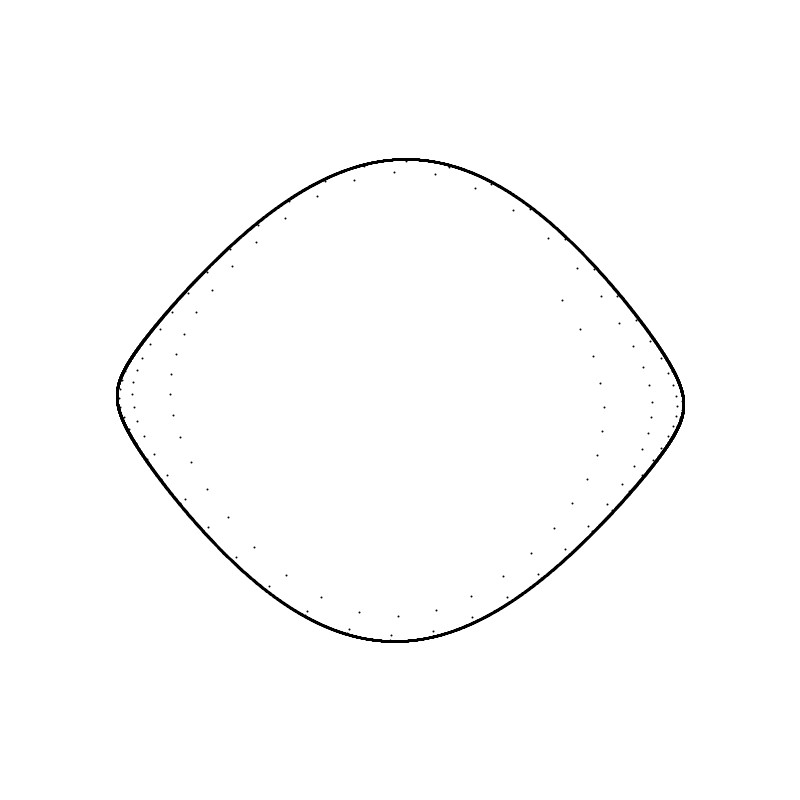
Der 0-dimensionale Attraktor zu Beginn (der Ursprung des Phasendiagramms) hat sich in einen 1-dimensionalen verwandelt. Wenn, wie hier, die Entstehung des folgenden Wertes aus dem alten Wert und der Änderung in Winkel und Geschwindigkeit in diesem Moment bestimmt wird, dann nennt man eine derartige Folge semikontinuierlich. Bleibt die Frage: Was genau tun wir physikalisch, wenn wir Δt vergrößern? Im nächsten Abschnitt "Kicked Rotator" wird genau dieser Sachverhalt diskutiert werden: Wir interpretieren Δt als den Zeitraum, in dem eine äußere Kraft das Pendel dazu zwingt, die aktuelle Änderung in Richtung und Größe über den nun längeren Zeitraum beizubehalten.
Sketch Mathematisches Pendel (kleine Ausschläge).
Sketch Mathematisches Pendel (beliebige Ausschläge).
Sketch Mathematisches Pendel Semikontinuierlich (Kicked Rotator).
Menu