3D-Animationen
Lissajous-Figuren in 3D
Wenn Sie nicht wissen, was Lissajous-Figuren sind, schauen Sie sich zunächst die Erklärungen im Kapitel Design für zwei Dimensionen an.
Im Gegensatz zum zweidimensionalen Lissajous-Bild, in dem die Summe zweier Sinus-Funktionen mit zwei variablen
Frequenzen betrachtet wird, haben wir es hier mit drei Dimensionen zu tun. Das heißt, es gibt auch drei
Sinus-Funktionen mit drei variablen Frequenzen. Man muss nun die Funktionswerte der drei Funktionen auf den
zugehörigen Achsen eintragen. Hat man, abhängig von der Variablen w (=Winkel im Bogenmaß), dies in kleinen
Schritten für den gesamten Definitionsbereich getan, so entsteht eine Kurve im Raum. Im Bild sieht man das
Ergebnis - links für eine Farbe und rechts für einen Farbverlauf. Enttäuschenderweise sieht man selbst beim
Farbverlauf das Bild nicht wirklich dreidimensional. Man kann das zunächst dadurch verbessern, dass man
diese Linien rotieren lässt. Sehr anschaulich ist es dadurch aber noch immer nicht.
Dieses Problem werden wir gleich lösen. Doch schauen wir uns zunächst die drei Funktionen genauer an.

Die zugehörigen Formeln sind unter Punkt (1) aufgeführt.
A1 , A2 und A3 stehen für die Amplituden,
f1 ,f2 und f3 für die Frequenzen. w schließlich ist der Winkel-Variable.
Man kann die Menge der Überlagerungen erheblich vergrößern, wenn man die drei Funktionen geschickt erweitert.
Unter (2)
sind die Formeln aufgelistet, die eine Art Frequenz-Modulation von f1,f2 und f3 zulassen.
Dies erreicht man über die Parameter AMod1 , AMod2 und AMod3
Auf all diese Parameter können Sie, sofern Sie an einem Computer sitzen, im Sketch unten zugreifen.
Da im zweidimensionalen Fall die Bilder auf ganz andere Art entstanden sind, müssen wir noch festlegen,
wie man hier den Raum-Eindruck erhalten will.
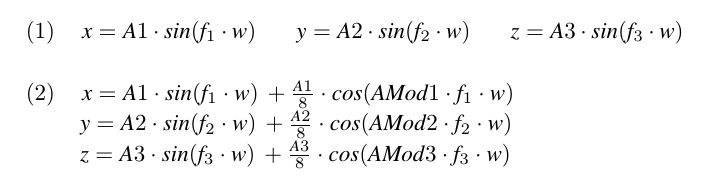
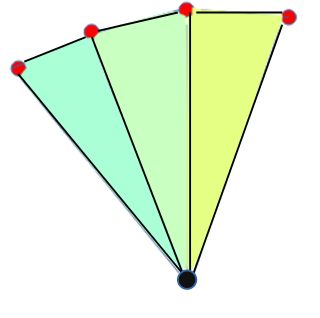
Man zeichnet vom Ursprung (im Bild links der schwarze kleine Kreis) zu zwei benachbarten Punkten ein
Dreieck. In Processing heißt der entsprechende Befehl TRIANGLE_FAN. Die so entstandenen Dreiecke färbt
man mithilfe eines Farbverlaufes.
Sehr schnell werden Sie bemerken, dass es dabei ein Problem gibt: Die Farben flackern heftig und es gibt
kein bleibendes Bild. Das liegt daran, dass die Kurve die Punkte nicht einen nach dem anderen erreicht,
sondern oftmals verharrt und sogar zurück läuft. Das dabei entstehende Flackern können wir verhindern,
indem wir jedem Dreieck, also immer zwei Kurvenpunkten, immer eine feste Nummer des Farbverlaufs zuordnen.
Bleibt das Problem, dass,
wie oben schon erwähnt,
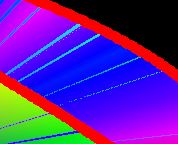
bei der Entstehung der Kurve mitunter eine relativ
große Verweildauer in einer kleinen Umgebung stattfindet. Dadurch entstehen kleine Farbinseln (Bild links).
So kann man das vermeiden:
{ if(q.abstandVon(p)< 4) wegLassen = true; }
Auch das Gegenteil ist möglich, dass nämlich ein großer Sprung stattfindet. Diese beiden Punkte dann zu einem Dreieck zu verbinden, ist sinnlos. Also achten wir auch darauf, dass zwei Punkte eines Dreiecks einen bestimmten Abstand nicht überschreiten dürfen. Und so sieht der Code für das Zeichnen der Dreiecke aus:
noStroke();
strokeWeight(8);
neuStart =von;
l=von;
F=0;
beginShape(TRIANGLE_FAN);
while (l<=reduzAnzPkte-2){
if(F==4096)F=0;
D = lissajousPkte.get(l-1).abstandVon(lissajousPkte.get(l));
if(D< 15 ){//nächsterPunkt näher als D
fill(farben4096[F],255);
vertex(0, 0, 0);
vertex(lissajousPkte.get(l).x, lissajousPkte.get(l).y, lissajousPkte.get(l).z);
vertex(lissajousPkte.get(l+1).x, lissajousPkte.get(l+1).y, lissajousPkte.get(l+1).z);
}else{//nächster Punkt weiter als D entfernt - würde zu falschen Verbindungen führen
if(l>=reduzAnzPkte) neuStart = reduzAnzPkte;
else neuStart= l+1;//starte bei nächstem Punkt neu!
break;
}
l++;
F++;
if(l==reduzAnzPkte-1)neuStart=reduzAnzPkte;//beendet die while-Schleife lissajous3DZeichnen(neuStart)
}
endShape();
}
Der Sketch startet mit den Frequenzen f1=3, f2=6 und f3=7.
Mit folgenden Tasten können Sie die Parameter des Sketches ändern:
| Tastenaktion | Wirkung |
|---|---|
| Taste 1 | Frequenzen f1 um 1 erhöhen |
| Taste 2 | Frequenzen f2 um 1 erhöhen |
| Taste 3 | Frequenzen f3 um 1 erhöhen |
| Taste l | Lissajous Funktionen / erweiterte trigonometerische Funktionen |
| Taste k | Kurve mit Dreiecken / Nur Kurve |
| Taste f | Farbverlauf ändern |
| Taste s | roter Rand / farbiger Rand |

Im Bild links sehen Sie zwei Sonderfälle. Ganz links ist f1 = f2.
Die Figur wird nur noch zweidimensional. Rechts daneben ist f1 = f2 = f3.
Damit ist die Überlagerung eindimensional.
Schauen Sie sich auch die
GeoGebra-Seite an. Interessant sind
dort vor allem die Projektionen auf die drei Koordinaten-Ebenen, die exakt den Ergebnissen des zweidimensionalen
Falls entsprechen.
Sollten Sie sich für den Namensgeber Jules Lissajous interessieren, so finden Sie hier weitere
Informationen:
Jules Antoinde Lissajous
Menu