3D mit Processing
Explizite Flächen
Lesen Sie zunächst auf der Übersichtsseite
Analytische Flächen
die Definition einer Expliziten Fläche durch!
Charakteristisch ist hier vor allem die Eigenschaft, dass die x- und y-Werte der Bildpunkte im Raum
genau den x- und y-Werten der Definitionsmenge entsprechen:
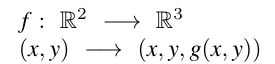
Die Funktion g ordnet allen Punkten der ebenen Definitionsmenge genau einen Wert g(x,y) = z zu.
Eine explizite Fläche kann man sich anschaulich so vorstellen:
Um die Anwendungen auch mit einem Smartphone zu nutzen, wurden hier einige virtuelle Tasten
verwendet. Mit deren Hilfe kann man beispielsweise die Flächen um alle drei Achsen rotieren lassen.
Um die Raumpunkte zu berechnen, benutzt man eine doppelte Schleife, die über alle Gitterpunkte läuft.
Die x- und y-Werte muss man noch durch den map-Befehl anpassen. Da man den Abstand des Gitterpunktes
vom Ursprung für die Farbgebung gut gebrauchen kann, wird der Wert hier in r gespeichert.
Unter switch legen wir die Gegebenheiten für die z-Werte ab. Im nachfolgenden Sketch
haben Sie neun Wahlmöglichkeiten.
for (int iy = 0; iy <= anzahlY; iy++) {
for (int ix = 0; ix <= anzahlX; ix++) {
x = map(ix, 0, anzahlX, xMin, xMax);
y = map(iy, 0, anzahlY, yMin, yMax);//Pixel(ix,iy) auf eKoordinatensystem (x,y) abbilden
punkte[ix][iy] = new PVector();//enthält die unveränderten x und y eKoordinaten
punkte[ix][iy].x = x;
punkte[ix][iy].y = y;
r = sqrt(x*x + y*y);//Abstand vom Ursprung in der Ebene
switch(wahlFunktion){
//case 1 bis case 9
}
}
}
}
| Tasten- oder Mausaktion | Wirkung |
|---|---|
| Taste w | nächste Fläche |
| Taste x | Drehung x-Achse start/stopp |
| Taste y | Drehung y-Achse start/stopp |
| Taste z | Drehung z-Achse start/stopp |
| Tasten g | Gitterlinien anzeigen |
| Tasten + | zoom in |
| Taste s | Hintergrund schwarz/weiß |
| Taste a | Anzahl der Gitterpunkte erhöhen |
| Taste A | Anzahl der Gitterpunkte verringern |
| in das Bild klicken | zoom out |
Wenn man ins Bild zoomt, können die Tasten eventuell verdeckt werden. Mit der Option "in das Bild klicken" können die Tasten wieder sichtbar gemacht werden.
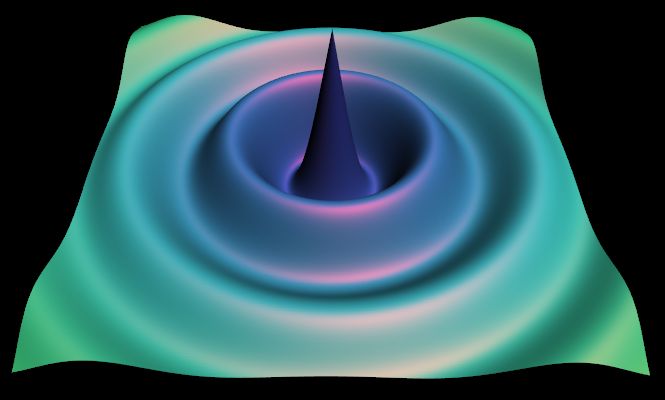
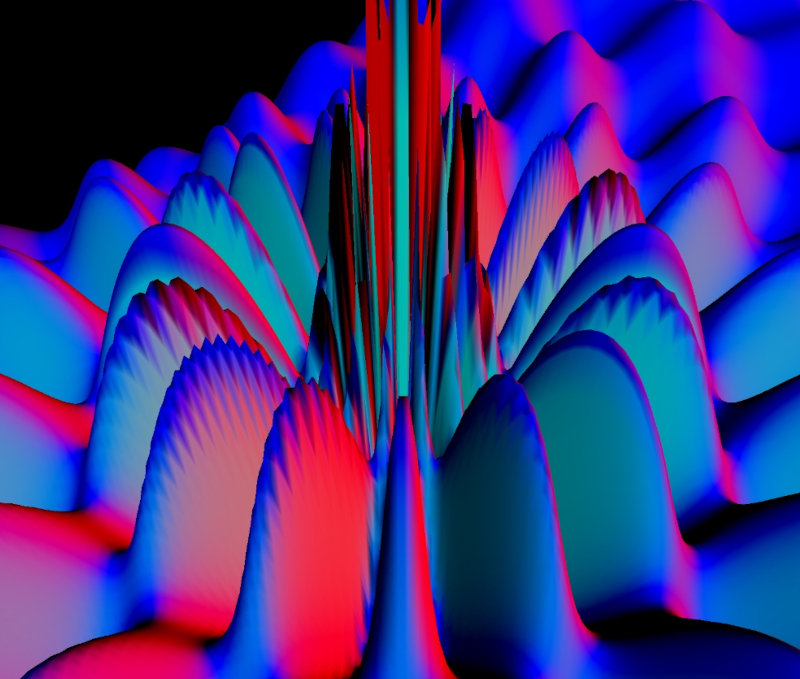
Das obige Bild ist ein Screenshot von Funktion 6 (siehe weiter unten). Die Farben sind nach einer Regel festgelegt:
Oberflächenelemente senkrecht zu x-Achse: rot
Oberflächenelemente senkrecht zu y-Achse: grün
Oberflächenelemente senkrecht zu z-Achse: blau
Bitte beachten: Je größer die Anzahl der Gitterpunkte, desto langsamer die Drehungen.
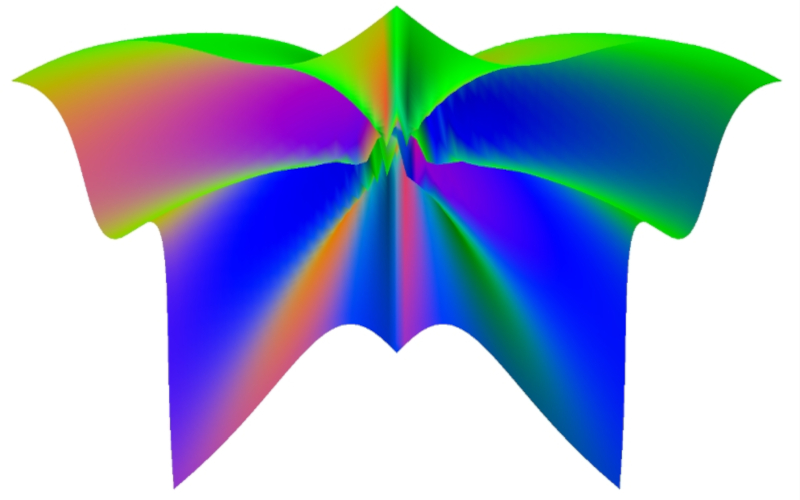
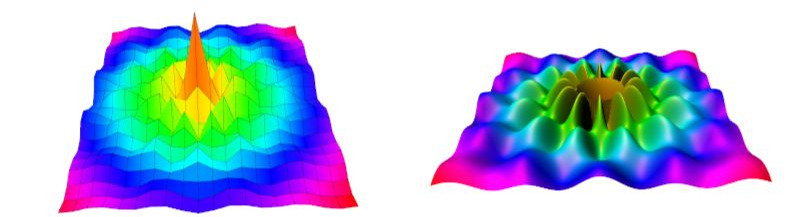
In folgendem Bild (Vergrößerung von Funktion 3) sehen Sie, dass die Anzahl der Gitterpunkte die Genauigkeit
der Darstellung einer expliziten Fläche ganz wesentlich bestimmt.
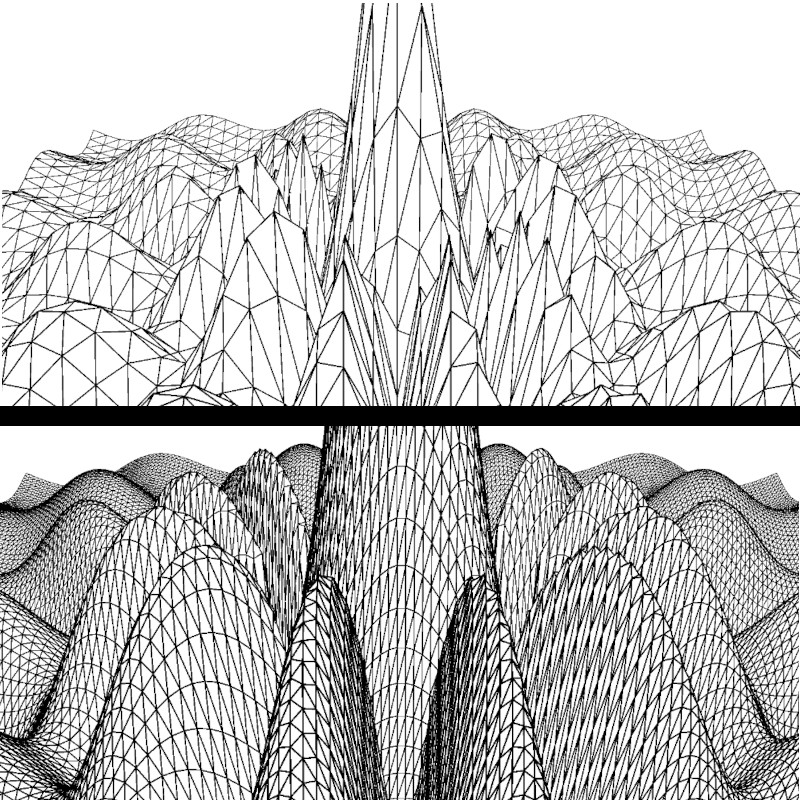
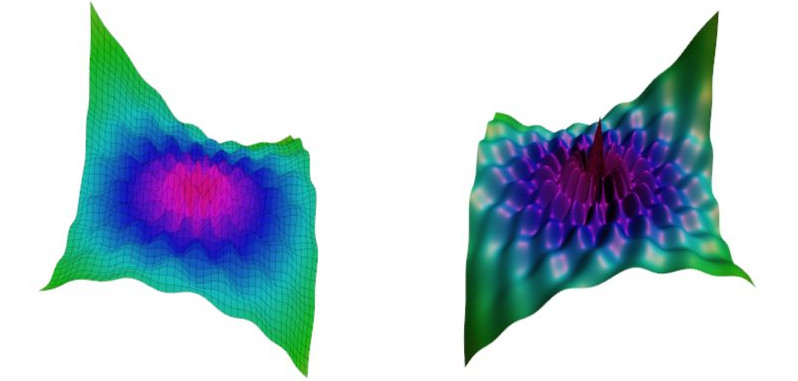
Auch starke Vergrößerungen, wie im nächsten Bild (Funktion 5 Unterseite), bergen mitunter einige Überraschungen.
Hier etwa bekommt man bei großer Anzahl von Gitterpunkten Strukturen zu sehen, die bei geringer Auflösung
"glatt gebügelt" wurden.
Um Grids zu zeichnen, verwenden wir die im Lehrbuch im 14. Kapitel erläuterte Methode:
pg.beginShape(QUAD_STRIP); //oder: pg.beginShape(TRIANGLE_STRIP);}
for (int ix = 0; ix < anzahlX+1; ix++) {
quadsFaerben(ix,iy);}
pg.vertex( punkte[ix][iy].x , punkte[ix][iy].y , punkte[ix][iy].z );
pg.vertex(punkte[ix][iy+1].x , punkte[ix][iy+1].y , punkte[ix][iy+1].z );
pg.endShape();
Hier nun die 9 Funktionen. Die 3D-Darstellung ohne Gitterlinien sehen hier nicht so plastisch aus, wie in den Bildern unten. Das liegt daran, dass die Anwendung hier im Browser in Java-Script geschrieben ist. Zwar gibt es auch dort "directionalLight()", wenn man mit WEBGL arbeitet. Nur leider sind die Ergebnisse in Processing deutlich besser.
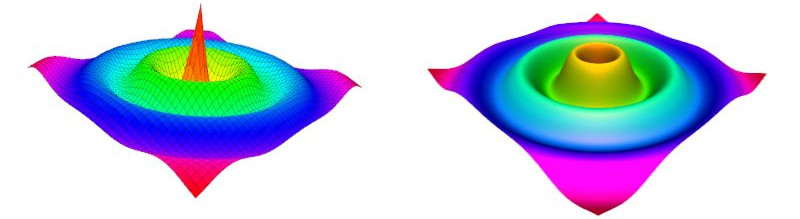
punkte[ix][iy].z = 6* cos(1.5*r)/(r+1);
punkte[ix][iy].z = 8* cos(1.5*r)/(r+1) + 0.05*x*y - 0.01*x*x + 0.01*y*y + 2*abs(sin(2*alpha));
Funktion 2:
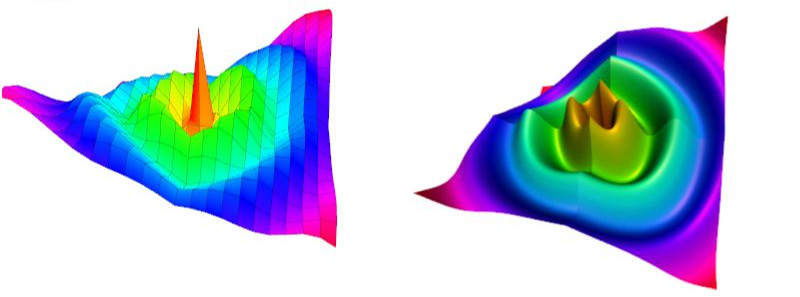
Funktion 3:
if(r>2) punkte[ix][iy].z = 8*cos(r)*sin(12*alpha+PI/2)/(r+1);
else punkte[ix][iy].z = 8*cos(r)/(r+1);
Funktion 4:
punkte[ix][iy].z = 0.06*r*r*cos(0.8*r)*cos(12*alpha);

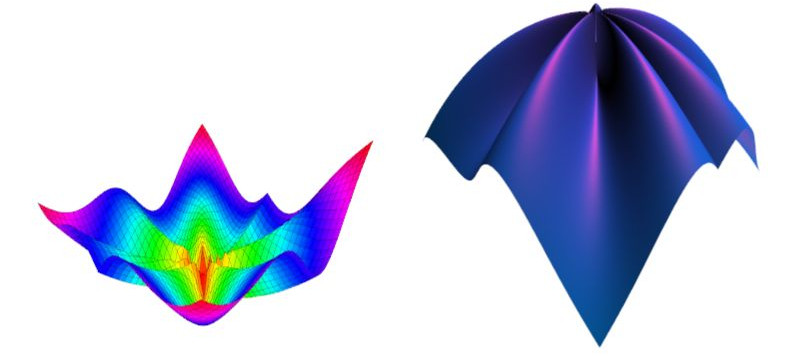
Funktion 5:
punkte[ix][iy].z = 0.003*(x*y+2*x*x*y-2*x*y*y)+ 6*cos(1.5*r)*cos(16*alpha)/(r+1);
Funktion 6:
punkte[ix][iy].z = 0.05*(36-r*r)+8-2*sin(6*alpha);;
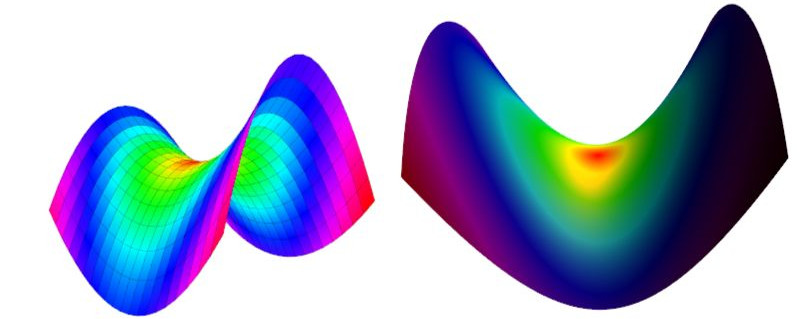
Funktion 7:
punkte[ix][iy].z = sq(y)/16-sq(x)/9;
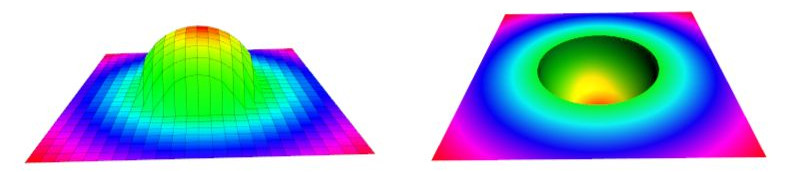
Funktion 8:
if(-sq(x)-sq(y)+25 >=0)punkte[ix][iy].z = sqrt(-sq(x)-sq(y)+25);
else punkte[ix][iy].z = 0;
Menu