Menu

Attraktore

De Jong Attraktor

Grundlagen

Vorab:
Der De Jong Attraktor unterscheidet sich nur wenig vom Clifford Attraktor. Daher werden die Erkärungen hier etwas knapper ausfallen. Wer es genauer wissen will, schaut sich die entsprechende Stelle im Kapitel Clifford Attraktor an.

Die Iteration

Die Parameter a,b,c und d wählt man aus dem Bereich von -2.5 bis +2.5; Da auch hier möglicherweise mehrere Millionen Mal iteriert werden muss, sollte man mit double-Attributen arbeiten. Dies ist auch bei der Sinus- und Cosinusfunktion möglich, sofern man mit die Klasse Math verwendet.
Worin unterscheidet sich dieser Attraktor vom Clifford bzw. vom Henon Attraktor?
Um das zu klären, müssen einige Fragen bezüglich der Erzeugung des Attraktors beantwortet werden:

• Spielt der Startpunkt eine wesentliche Rolle?
  Welche Rolle spielen die Parameter a,b,c und d?
  Haben wir es mit einem Fraktal zu tun?
  

Mit der folgenden Anwendung können Sie dies testen:
(Zu Beginn a = -0.76937; b = 1.86306; c = 1.38907; d = 1.58330;)

Tasten- oder Klickaktion	Wirkung
Taste n	Anzahl der Folgepunkte verdoppeln
Taste h	Hintergrund s/w umschalten
Taste p	Umschalten Zoomen/Startpunkt
Taste z	Zufällige Parameter a,b,c,d
Taste s	Neustart
Klick ins Bild	hier Zoomen/Startpunkt setzen

Drückt man die Taste p, so bewirkt ein Klick ins Bild die Wahl des Startpunktes an dieser Stelle. (Drückt man erneut auf p, kommt man wieder in den Zoom-Modus.)
Im Bild links wurden fünf Starpunkte gewählt.
Bei jedem neuen Startpunkt wurde die Farbe gewechselt. Wir erkennen an den verschiedenen Farben, dass alle Folgepunkte im "wolkigen" Attraktor liegen, - aber öfters andere Stellen dort besetzen. Dies ist für unser weiteres Vorgehen wichtig. Da später hunderte von Millionen Punkte berechnet werden sollen, sollte man multithreaded arbeiten, in dem man jedem Core mit einem anderen Startpunkt beschäftigt.

Um zufällige Parameter zu wählen, verwendet man die Taste z. Wundern Sie sich nicht, wenn Sie oftmals nur einzelne Punkte sehen.

Klicken Sie so lange auf Taste z, bis Sie einen Attraktor ähnlich wie im Bild oben links sehen. Wie im Fall des Henon-Attraktors, zoomen Sie auf benachbarte Linie. Diese werden sich bei jeder weiteren Vergrößerung in mehrere Linien auflösen (Bild oben rechts). Gegebenenfalls mehrfach mit Taste n die Anzahl der Punkte erhöhen!
Damit sind die Fragen 2 und 3 beantwortet: Ein derartiger Attraktor ist bei der Wahl bestimmter Parameter ein Fraktal. Außerdem haben wir festgestellt, dass die Art des Attraktors massiv von der Wahl der Parameter a,b,c und d abhängt. Man bekommt mitunter einzelne Punkt-Attraktoren und auch geschlossene Linien, die nicht fraktal sind.

Trefferdichte

Sucht man im Internet nach "De Long Attraktor" bekommt man zumeist sehr ästhetische und äußerst ansprechende Bilder zu sehen. Diese können unmöglich in der oben beschriebenen Weise erzeugt worden sein. Es handelt sich dabei um sogenannte "Dichtebilder", also die Anzahl der Treffer auf einem Pixel. Die Idee ist simpel: Nehmen wir an, wir möchte ein Bild mit 1600 x 1600 Pixeln erzeugen. Dann benötigen wir einen 2-dimensionalen Array:

Jedem Pixel entspricht also ein Integer-Wert des Arrays und umgekehrt. Haben wir beispielsweise 8 Core zur freien Verfügung, dann ist jeder Thread für 200 x 1600 Startwerte zuständig. Da die ersten Werte meist nicht auch schon im Attraktor liegen, beachten wir die ersten zum Beispiel 10 Iterationsergebnisse nicht ("Leerlauf"). Außerdem werden die Werte, die nicht im Bildbereich liegen, weggelassen. Das Attribut m = 256 gibt an, wieviele Folgepunkte ab dem 10. Iterationsschritt noch zu berechnen sind. Natürlich muss man diesen Wert im Sketch veränden können. Er bestimmt ja die Gesamtzahl der Punkte und somit auch die Punktdichte. Mit den oben angegebenen Werten werden ca. 82 Millionen Punkte erzeugt. Bei einem Bild der Größe 1600x1600 sind das im Schnitt 32 Treffer pro Zelle. Um die Unterschiede in der Trefferzahl sichtbar zu machen, muss außer der Farbe auch noch die Transparenz einbezogen werden.
Jeder Thread bekommt einen eigenen Teil des Bildes zugewiesen, aus dem er zufällig die Anfangspunkte wählt. Vergessen Sie nicht, falls Sie die herunterladbaren Sketche verwenden, die Anzahl der Threads anzupassen. Hat man beispielsweise 8 Cores (virtuelle werden mitgezählt), dann sollte man die Anzahl auf 6 einstellen. Sind alle Threads fertig, addiert man alle Trefferergebnisse im Array MatrixHisto. Je nach Anzahl der restlichen Iterationen, bekommt man dann einen in bestimmten Bereichen gut "gefüllten" Array. In einem konkreten Fall gab es bei 2,56 Millionen Zellen beispielsweise 520000 Zellen, die nur einen Treffer hatten. 13 Zellen hingegen hatten 250 Treffer. Diese Spannweite gilt es mit geeigneter Farbgebung sichtbar zu machen. Man verwendet also die Dichte der Treffer für die Farbgebung. Wir erzeugen dazu einen Farbverlauf mit 2048 Stufen. Eine mögliche Einfärbung des Pixel kann dann so ausssehen: Die verwendeten Parameter bei folgendem Bild werden mit ausgegeben:

Für ein schwarz-weiß Bild verwenden wir folgenden äußerst simplen Algorithmus:
Höhere Trefferzahlen als 245 werden auf 245 gesetzt. Dies erspart uns die Verwendung von Transparenz.
Die Parameter bei folgendem Bild:

Möchte man etwas kompaktere Farben haben, dann wird man auf den Gedanken kommen, die Transparenz auch bei hoher Trefferzahl wegzulassen. Im letzten Kapitel wurde dargelegt, weshalb der Versuch zu keinem guten Ergebnis führen wird.
Weil die Anzahl der Zellen mit einer bestimmten Anzahl von Treffern äußerst ungleichmäßig ist,muss man die Zuordnung Anzahl Zellen mit x Treffern -> Farbwert ändern:
so bekommt man angenähert eine Gerade. Mit einem Farbberlauf color farbe2[] hat man dann Die zugehörigen Parameter bei folgendem Bild:
a = -1.7973 ;b = 1.2248 ;c = 0.8867 ;d = 2.4834;

Klassifikation mit Hilfe von Fixpunkten

Auf der Suche nach ästhetischen Dichtebildern staunt man einigermaßen, wie sehr sich die Ergebnisse durch eine neue Wahl von Parametern ändern. Ergebnisse wie die Dichtebilder oben sind eher selten anzutreffen. Mitunter sieht man schlicht gar nichts, weil nur ein winziges Pixel angezeigt wird. Das liegt dann daran, dass es nur Fixpunkte gibt. Wenn man Folgepunkte erst ab zum Beispiel n = 100 eintragen lässt, dann befinden sie sich möglicherweise so nah an den Fixpunkten, dass der Abstand aller weiteren Folgenelemente zu den Fixpunkten weniger als einem Pixel entspricht.
Wir werden sehen, dass sich die De Jongs Attraktoren auf elegante Weise klassifizieren lassen, wenn man die Anzahl und Art der Fixpunkte bestimmt. Dazu verwenden wir einen einfachen Trick: Es werden eine Anzahl zufälliger Startpunkt erzeugt, deren Folgepunkte aber erst ab n = 1000000 im Bild eingetragen. Das Ergebnis zeigt dann sofort, ob Fixpunkte vorliegen oder nicht. Und das wollen wir uns nun etwas genauer ansehen. (Es empfiehlt sich auch hier, mit doppelter Genauigkeit zu rechnen.)

Gegeben: a = 2.47533; b = 1.80892; c = 1.08907; d = 0.84880; Wir begnügen uns hier mit nur einem Startpunkt (unten, blau):

Der Startpunkt wurde eine Million mal iteriert. Die danach folgenden 200 Punkte verteilen sich unregelmäßig auf dem De Jong Attraktor (Dichtebild). Da sich nach einer Million Iterationen noch immer keine Punktanhäufungen an einer oder mehreren Stellen zeigen, dürfen wir annehmen: Es gibt hier keine Fixpunkte! Ebenfalls ist zu erkennen, dass die Punkte nur auf massiven Linien landen. Wenn man die Punkte erst ab einer höheren Anzahl von Iterationen einträgt, dann würde der transparente Bereich komplett verschwinden.

Bei den Clifford Attraktoren haben wir verschiedene Fixpunkt-Situationen gezeigt. Wir beschränken uns bei den De Jong Attraktoren auf ein einziges Beispiel. Es hat drei Fixpunktmengen, eine mit 3, eine mit 6 und eine mit 16 Fixpunkten. Die zugehörigen Parameter sind hier: a = -1.2342038; b = 2.1405172; c = 1.0269723; d = 0.95824766;


Blau: Fixpunktmenge aus 3 Fixpunkten
Rot: Fixpunktmenge aus 6 Fixpunkten
Grün: Fixpunktmenge aus 4 Fixpunkten

Von daher gibt es drei Farbbereiche, je nach dem, wo der Startpunkt landet. Die Helligkeit jedes Farbbereichs misst die Konvergenzgeschwindigkeit.
Auch ohne Vergrößerung erkennt man, dass die Farben und damit die Zuordnungen chaotisch verteilt sind. Wenn man Treffer erst ab einer hinreichend großen Zahl im Bild einträgt, dann verschwinden die rosa Punkte immer mehr. Sie ziehen sich sozusagen in die Fixpunkte zurück.

De Jong Gleichungen als partielle Ableitungen interpretiert

Bisher wurde jeder neue Punkt allein mit Hilfe des vorherigen Punktes bestimmt. Um einen neuen Attraktor zu bekommen, musste mindestens einer der vier Parameter a,b,c oder d geändert werden.
Nun soll ein System beschrieben werden, das erlaubt, den nächsten Punkt näherungsweise aus dem vorherigen Punkt und aus der Ableitung an diesem Punkt zu berechnen. Dazu verwenden wir die Euler-Methode:

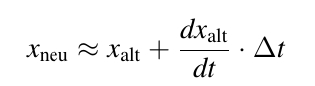
Normalerweise bemüht man sich um ein sehr kleines Δt . Interessanter wird es in unserem Fall, wenn man Δt etwas größer wählt, denn dann ähneln die Gleichungen den Gleichungen bei erzwungenen Schwingungen. Wie wir wissen, kann man dort chaotisches Verhalten erwarten. Und so sehen die partiellen Gleichungen nun aus:

Δt wird dort "delta" genannt. Für einen kurzen Test genügt es, die obigen Gleichungen in den Sketch De Jong Attraktor Multi Thread dieses Kapitels einzusetzen. Variieren Sie Δt zwischen 0.1 und 1.7. Entscheidend ist dabei eine Erkenntis: Die Attraktoren sind vom Startpunkt abhängig!
Etliche Fraktale werden durch die "Konvergenzgeschwindigkeit" eines Startpunktes erzeugt. Allen voran die Mandelbrotmenge. Divergenz in dem Sinn, dass die Punkte bei Anwendung der obigen Gleichungen gegen Unendlich streben, könne wir allerdings nicht erwarten. Andererseits wird es nur in einem Fall Konvergenz geben: Genau dann, wenn ein oder mehrere einzelne Fixpunkte existieren. Die zugehörigen Pixel werden schwarz gefärbt. Diese muss man aber nicht, wie oben, mühsam zuerst bestimmen. Es reicht uns, wenn zwei aufeinander folgende Punkte einen Abstand kleiner als zum Beispiel ein Millionstel besitzen. Ein Beweis für Konvergenz ist das freilich nicht. Denken Sie sich eine Fixpunktmenge bestehend aus zwei Punkten, die besagten Abstand haben. Dennoch dürfte es in den meisten Fällen korrekt sein.
Als Startpunkte verwenden wir die den Pixeln entsprechenden Punkte. Was aber soll mit "Fixpunktmengen" und "ausgedehnten unendlichen Punktmengen" geschehen? Wie soll man prüfen, wohin sich eine Punktfolge bewegt? (Für deren Definition lesen sie den obigen Abschnitt "Klassifikation...").
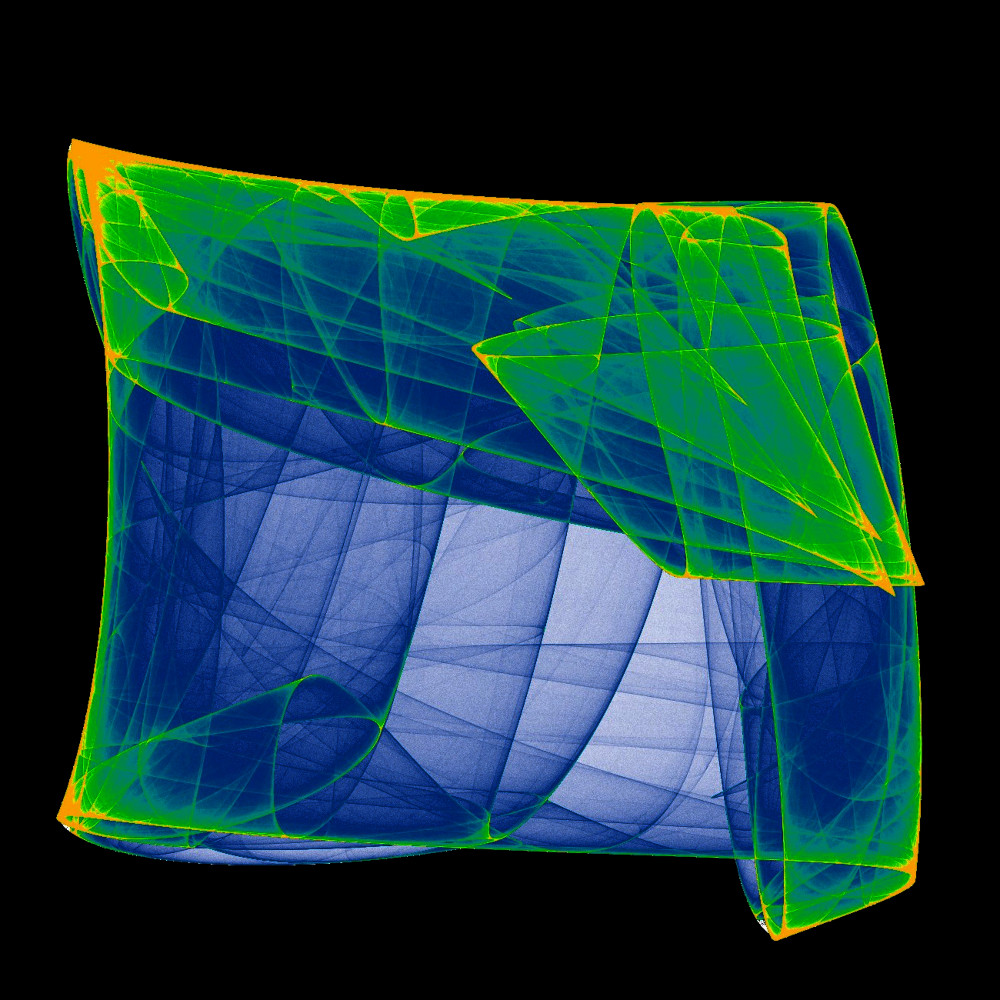
Es gilt also einen Unterschied zu finden, der sich beim Gang zu verschiedenen Fixpunktmengen ergibt. Da ist zunächst der zurückgelegten Gesamtweg und zum anderen der gesamte Winkel. Bei jeder Interation kann man einen Winkel dadurch bestimmen, dass man den Winkel der Strecke von Punkt P_n zu P_n+1 zur x-Achse misst. Da es auch negative Winkel gibt, muss man die Winkelsumme größenmäßig durch einen geeigneten Faktor an die Gesamtlänge anpassen. Die so entstandene Zahl wird einer Farbe zugeordnet. Diese Methode liefert für die Parameter:
a = 1.5207639; b = 0.86242867; c = 1.2873003; d = 0.6905384 und delta = 1.4   folgendes Bild:


Die Ecke links unten ist (-20,-20) und die rechts oben (20,20). Wie man sieht, funktioniert diese Methode recht gut. In manchen Gebieten ändert sich wenig,- es gibt aber auch möglicherweise fraktale Bereiche (Bildmitte).
Die dicken (point(11) farbigen Punkte entstanden durch Zeichnung von 50000 Folgepunkte nach einer Million Iterationen. Einzelne Punkte in der schwarzen Mitte sind offensichtlich Fixpunkte. Die anderen farbigen Punkte gehören zu Fixpunktmengen verschiedener Anzahl. Die weißen Gebilde sind ausgedehnte unendliche Mengen, wie wir sie für die Dichtezeichnung der Attraktoren schon verwendet haben.
Um die Korrektheit der Farbgebung zu kontrollieren, wählen Sie eigene Startpunkte. Hierfür laden Sie den Sketch De Jong Gleichungen als Ableitungen runter. Nach dem Start erscheint nach einiger Zeit ein Bild. Den Startpunkt wählen Sie durch einen Rechtsklick an der gewünschten Stelle. Will man lediglich die Punkte ab der 1000000-ten Iteration sehen, so klickt man zuvor auf die Taste 'X'.


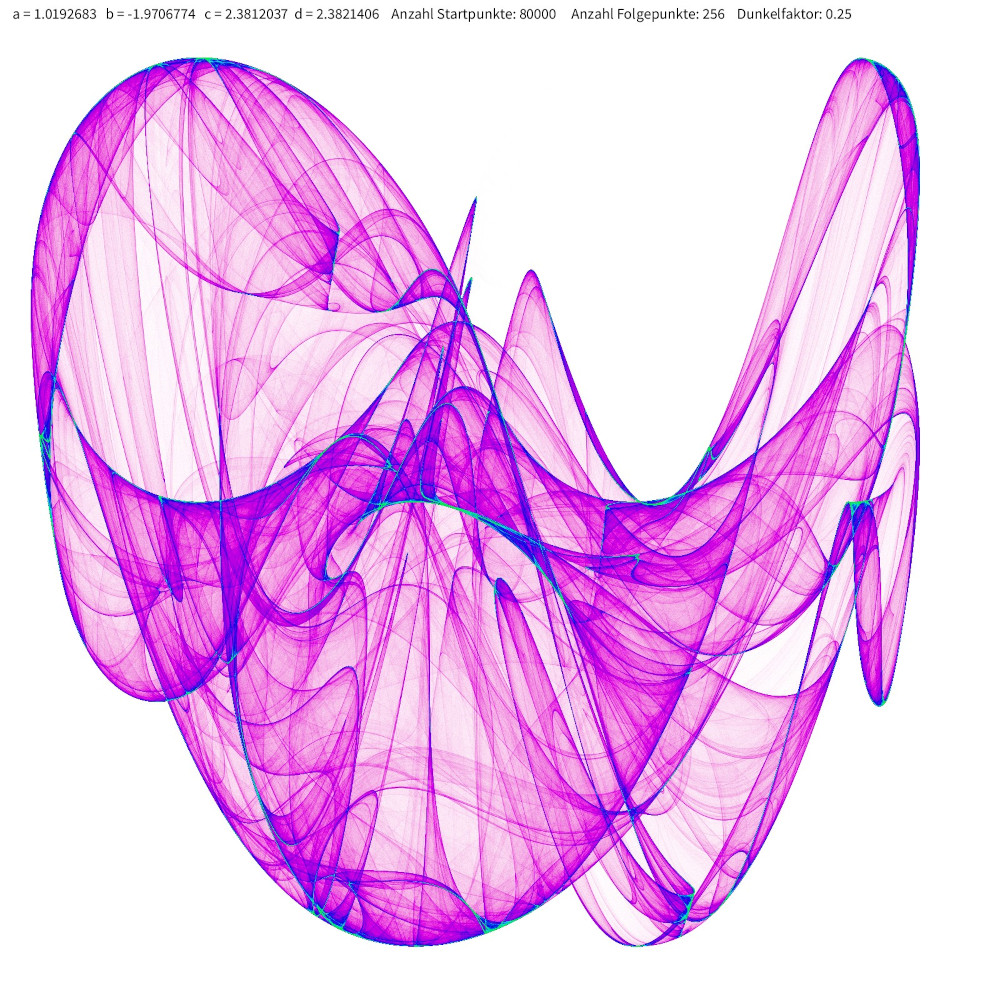
Links delta = 1.3 , rechts delta = 1.4. Man bekommt, wie bereits angedeutet, für identische Paramter verschiedene Attraktoren, sobald man delta ändert. Das nutzen wir, um wie im Abschnitt Trefferdichte ästhetischere De Jong Attraktorenbilder zu erzeugen. Dabei sind nur wenige Änderungen im Sketch De Jong Attraktor Multi Thread nötig: Das Zentrum ist nicht der Ursprung, sondern der ungefähre Mittelpunkt des zu zeichenden Attraktors. (Nicht vergessen, die Iterationsgleichungen anzupassen!) In den folgenden Bildern gelten immer noch die gleichen Parameter. Großes Bild: delta = 1.5.




Kleine Bilder von links oben nach rechts unten: delta = 1.0, delta = 1.1, delta = 1.2 und delta = 1.6.


Den bereits für diese Situation angepassten Sketch "De Jong Gleichungen Multi Thread als Ableitungen" können Sie unten runterladen.

Sketch De Jong Attraktor Single Thread

Sketch De Jong Attraktor Multi Thread

Klassifikation der De Jong Attraktoren

De Jong Gleichungen als Ableitungen

De Jong Gleichungen Multi Thread als Ableitungen

Menu