Dynamische Systeme
Doppelpendel ohne Schwerkraft
Ein mathematisches Pendel hat, wie bereits erwähnt,
zwei Freiheitsgrade. Da der Vorgang reibungsfrei ablaufen soll, gilt der Energieerhaltungssatz, der eine
Beziehung zwischen Winkel und Winkelgeschwindigkeit fordert. Daher bleibt hier nur ein Freiheitsgrad übrig.
Das zugehörige Phasendiagramm zeigt für jedes Endergieniveau entweder eine ellipsenförmige Figur
oder eine Welle, je nachdem, ob das Pendel nur schwingt oder sich überschlägt. Es kann hier weder chaotische
noch echte
quasiperiodische (= pseudoperiodische ) Schwingungen geben. Aber selbst in diesem einfachen Fall kann man einen Poincaré-Schnitt
erzeugen. Trägt man beispielsweise immer wenn das Pendel durch die Ruhelage schwingt, den Wert der Winkelgeschwindigkeit
ein, dann sähe man auf dem Schnittbild für jede Energie genau zwei symmetrisch zur Null liegende Punkte.
Wie schon im Abschnitt "Wege ins Chaos" dargestellt, hat man bei einem Doppelpendel das im schwerefreien
Raum schwingt, zwei Freiheitsgrade und die Garantie, dass allenfalls pseudoperiodische Schwinungen entstehten.
Was also hindert uns, genau wie im Fall des mathematischen Pendels, ein
Phasendiagramm zu erstellen und zwar derart, dass für jeden neu errechneten Zustand ein Punkt eingetragen wird.

Das obige Bild ist ein auf diese Weise entstandenes "doppeltes Phasendiagramm". Hübsch anzuschauen, aber welche
Informationen liefert mir das Bild? Dabei ist dies ein noch recht "ordentliches" Bild. Versuchen Sie im folgenden
Sketch weitere deratige Diagramm zu erstellen. (Bei jedem Klick startet das Programm mit neuen Zufallswerten.
Rot wird für das obere und Grün für das untere Pendel verwendet.) Nachdem Sie in die Anwendung geklickt haben,
können Sie durch einen Klick in die rechte untere Ecke die Bewegung beschleunigen oder durch einen Klick in
die linke untere Ecke die Bewegung verlangsamen.
Sie werden verschiedene Bilder zu sehen bekommen:
Entweder wird im Laufe der Zeit ein großer Teil der Fläche ausgefüllt oder es entsteht ein Muster bei dem die
Trajektorien nach einer gewissen Zeit immer wieder auf ihre alten Spuren zurückkommen. Obwohl hier niemals
Chaos vorherrscht, ist in den meisten Phasendiagrammen recht wenig Information zu entnehmen. Im Poincaré-Schnitt
aber erhält man in diesem Fall entweder ein ellipsenförmiges
oder ein wellenförmiges Gebilde zu sehen. Zu erwähnen wäre allenfalls noch,
dass die ellipsenförmigen Linien nicht geschlossen sein müssen und dass die Lage der Form von der
Gesamtenergie abhängt.
(Siehe letztes Kapitel.)
Nicht immer ist das doppelte Phasendiagramm wertlos. In sehr seltenen Fällen sieht man sofort, was hier los
sein muss. Das folgend Bild zum Beispiel ist genau mit dem gleichen Sketch entstanden, wie die Animation
weiter oben, die Sie hoffentlich schon ausgiebig getestet haben.
Lediglich das Doppelpendel wurde weggelassen, damit schneller sehr viele Phasenpunkte errechnet
werden können (weiß ist die Null-Linie für die Winkelgeschwindigkeit des oberen Pendels) :
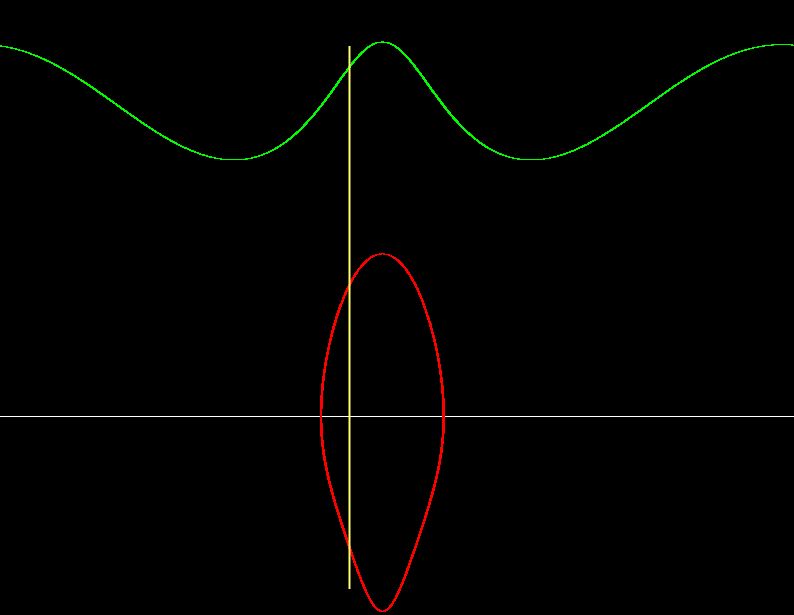
Es war zugebenermaßen recht mühsam einen passenden Startwert für die beiden Winkel und Winkelgeschwindigkeiten zu finden. Wenn Sie selber einen solchen Startpunkt finden möchten, nur zu! Andernfalls laden Sie sich den Sketch Doppelpendel ohne Schwerkraft Periodisch runter. Dort sind die "geheimen Werte" schon fertig eingetragen, so dass Sie überprüfen können, ob das obige Bild wirklich echt ist ...
Bleibt die Frage: Was sehen wir hier eigentlich? Ist das ein periodischer Fall? Die Antwort ist einfach: Nehmen Sie diese Anfangswerte und erstellen Sie einen Poincaré-Schnitt! (Gelbe senkrechte Linie). Maximal drei Punkte und minimal einen Punkt. Also eindeutig periodisch!
Im letzten Kapitel wurde ein Sketch für ein Doppelpendel im Schwerefeld vorgestellt. Man bekam dort einen Poincaré-Schnitt für das obere Pendel. Ihre Aufgabe könnte nun sein, den Sketch so umzuschreiben, dass ein Poincaré-Schnitt für das untere Pendel errechnet wird. Das folgende Bild ist bei E = 2500 entstanden.
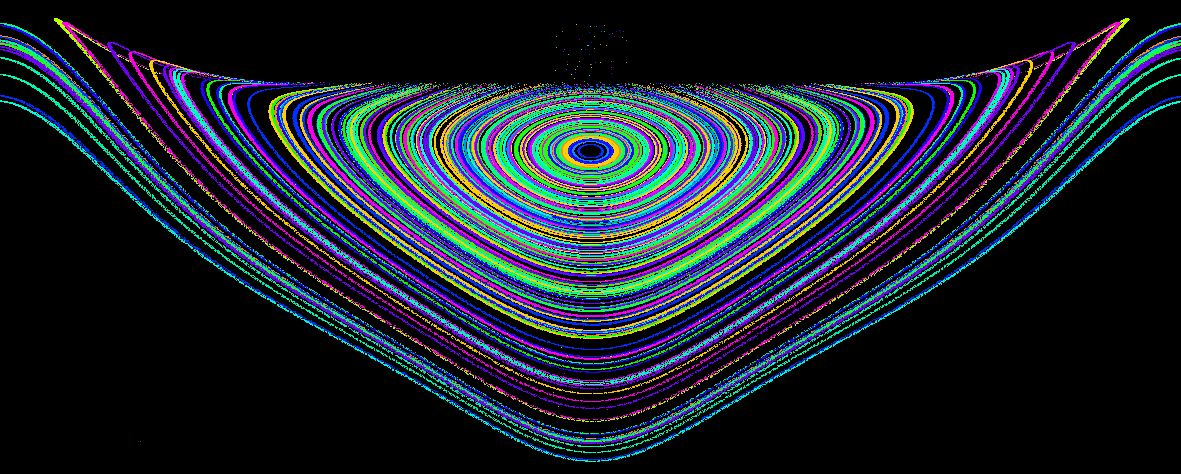
Damit man solch schmale Trajektorien bekommt, muss man den Zeitschritt dt sehr klein wählen.
Klein heißt hier in jedem Fall kleiner als 0.005 . Dies treibt den Rechenaufwand gewaltig in
die Höhe. Selbst mit einem Processor mit 16 Core und 4 GHz Taktfrequenz benötigt der Sketch, der den Processor
zu fast 100% auslastet, gut 5 Minuten.
Dennoch war die Genauigkeit möglicherweise noch nicht ausreichend. Es gibt in den oberen Ecken Überschneidungen
von Trajektorien. Das muss nicht notwendigerweise falsch sein. Denn immerhin gibt es zu zwei festgelegten
Winkeln und einer festen Winkelgeschwindigkeit wegen des Energie-Erhaltungssatzes
zwei Lösungen der quadratischen Gleichung für die zweite Winkelgeschwindigkeit. Es wäre allerdings zu prüfen,
ob dies hier auch zutrifft...
Sketch Doppelpendel ohne Schwerkraft Periodisch.
Sketch Poincaré-Schnitt für ein Doppelpendel (Threaded).
Menu