Fraktale: Fallen (Traps) 2
Welche Fallen für welche Fraktale?
 Zunächst muss festgelegt werden, in welchem Bereich das Fraktal gezeichnet werden soll. Genau in diesem Bereich
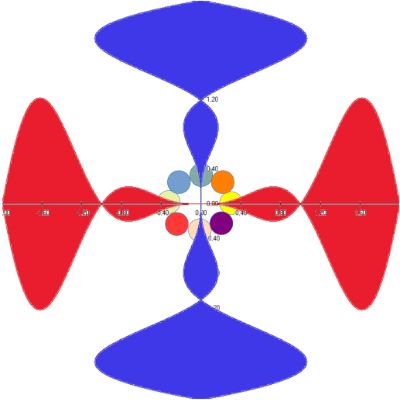
kann man nun die Fallen konstruieren. Wir schauen uns das am Beispiel eines Mandelbaum-Fraktals an. Im Bild links
sind einige Gebiete der Definitionsmenge (die Fallen) des Fraktals farbig eingetragen.
Die rote "Hantel" entsteht, wenn man alle
Punkte markiert, für die gilt:
Zunächst muss festgelegt werden, in welchem Bereich das Fraktal gezeichnet werden soll. Genau in diesem Bereich
kann man nun die Fallen konstruieren. Wir schauen uns das am Beispiel eines Mandelbaum-Fraktals an. Im Bild links
sind einige Gebiete der Definitionsmenge (die Fallen) des Fraktals farbig eingetragen.
Die rote "Hantel" entsteht, wenn man alle
Punkte markiert, für die gilt:
|yWert| <= |0.5*xWert*xWert*sin(PI*xWert|,
wobei yWert für den imaginären
und xWert für den reellen Wert der komplexen Zahl z der Definitionsmenge steht. Was diese Funktion
angeht, sind der Phantasie keine Grenzen gesetzt. Die blaue "Hantel" ist die rote Hantel um 900 gedreht.
In der Mitte schließlich sind 8 Fallen in der Form von Kreisen platziert. Die verwendeten Farben sollen zwei Dinge
ausdrücken. Erstens wird damit verdeutlicht, dass alle Punkte, die in einer Falle landen, genau einen Farbwert
zugeordnet bekommen. Es wird lediglich die Helligkeit in Abhängigkeit von der Entfernung von der Achse bzw. dem
Kreismittelpunkt variiert. Zweitens kann man erkennen, dass beispielsweise die rote Hantel zwei Kreise teilweise
abdeckt. Das passiert dann, wenn man zuerst die Hantel-Falle testet. Landet ein Punkt dort, dann wird die Iteration
abgebrochen und es ist somit gleichgültig, dass dort auch eine Kreis-Falle liegt.
Sinus-Kreise-Traps für Mandelbrot-Fraktale
Im ersten Bild unten sehen Sie die Wirkung der obigen Traps auf das Standard-Mandelbrot-Fraktal
z -> z2 + c.
Auch hier lässt die Farbtafel-Klasse unzählige Einfärbungen zu. Im zweiten Bild beispielsweise wurden die Kreis-Traps
mit knalligen Farben markiert. Experimentieren Sie auch mit anderen Farbzuordnungen.
Die im Sketch benutzte Iteration
für das Standard-Mandelbrot-Fraktal (z -> z2 + c mit erstem Bild) sollte ebenfalls variiert werden
(z.B.: z -> z3 + c mit zweitem Bild).
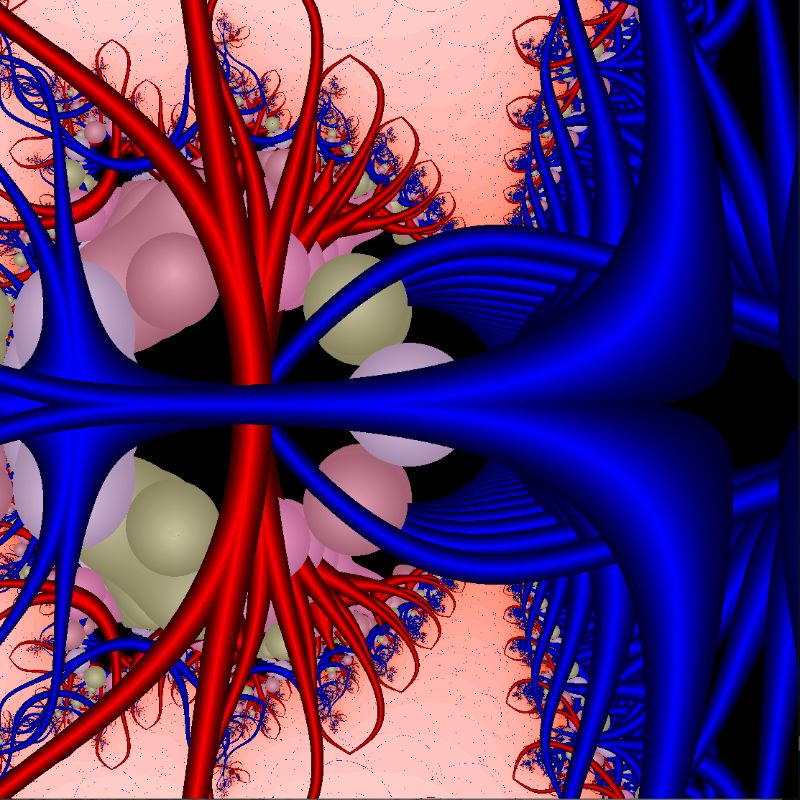
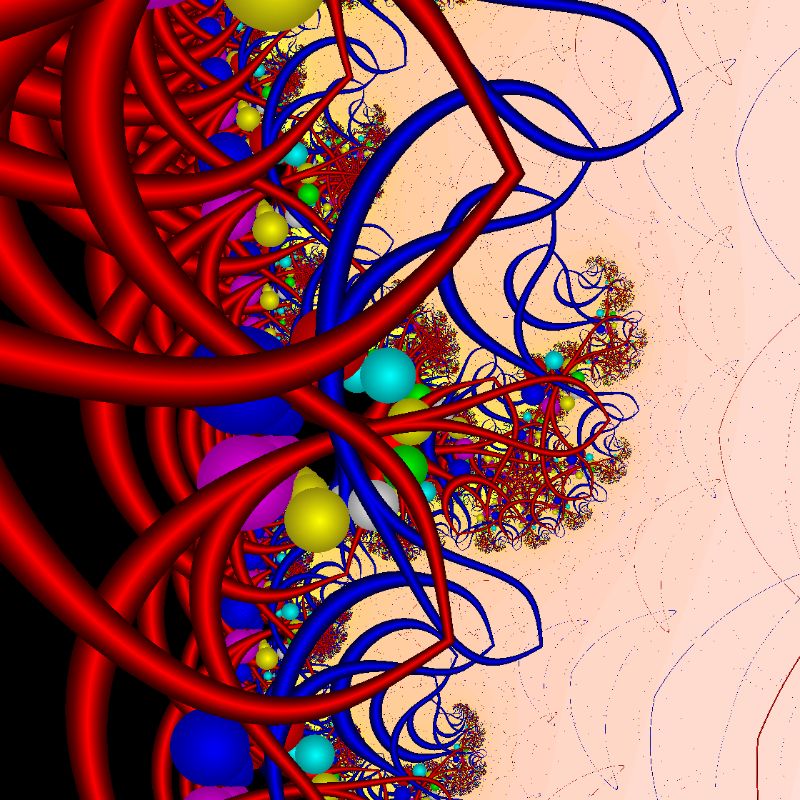

MandelbrotTrappedSinusXYKreise
Ringe-Kreise-Traps für Julia-Fraktal
Im zweiten Beispiel bestehen die Fallen aus mehreren konzentrischen Ringen und acht Kreisen. Die im Sketch benutzte Iteration für die Julia-Fraktale sind: z -> z3 + c und z -> z4 + c

Julia3TrappedRingeKreise

Julia4TrappedGitterKreise
Verschiedene Traps für Newton-Fraktale
Bevor Sie weiterarbeiten, schauen Sie sich das Kapitel
Julia- und Fatou-Mengen an. Wir verwenden hier nämlich
die dort gezeigten Newton-Julia-Sketche. Auch ohne die zu programmierenden Traps sind die Sketche
bereits jetzt recht
vielseitig verwendbar. Es ist also darauf zu achten, dass die Programme nach der Erweiterung nicht überladen werden.
Zunächst verwenden wir die Funktion f auf der Menge der komplexen Zahlen mit:
f(z) = z11+5z4-3z3 +c
Als Fallen verwenden wir die schon oben erwähnten "sinus-Hanteln". Außerdem einen schmalen Streifen um x-und y-Achse.
Die Nullstellen (also Fixpunkte der Newton-Iteration) kennzeichnen wir durch Kreise.
Diese Kreise stellen also keine Falle dar. (Um den Unterschied zu erkennen, sind beim dritten Bild die Kreise
als Fallen verwendet.)
Die Konstante c kann vom Benutzer zufällig gewählt werden.



JuliaNewton11
Wie verändern sich die Bilder, wenn man Sinus- und/oder Cosinus-Funktionen bei der Funktion f zulässt? Das folgende
Beispiel verwendet die Funktion f auf der Menge der komplexen Zahlen:
f(z) = z10+z5sin(z) + cos(z2) + c
Die folgenden beiden Bilder geben eine Vorstellung davon.


JuliaNewton10Sinus
Menu