Fraktale: Farbtafeln (color maps)
Konstruktion einer eigenen Farbtafel
Mathematisch betrachtet ist es ziemlich gleichgültig, wie die Ergebnisse der Iterationen in Farben umgesetzt werden. Hier
zählt nur, dass die Abbildung wesentliche Eigenschaften des Fraktals sichtbar macht. Ob das entstandene Bild
"esthetisch" oder "schön" ist, spielt hier keine Rolle. Zumal die beiden Eigenschaften mathematisch kaum quantifizierbar
wären. Auf der anderen Seite kann man sich, selbst wenn man nur mathematische Einsichten anstrebt,der Faszination
mancher Fraktale kaum entziehen. Die ersten Fraktale wurden mit Nadeldruckern in Computer-Papier gestanzt.
Hier dürfte sich die Begeisterung in Grenzen gehalten haben. Auch danach, wenn auch schon bunt, wurden die meisten
Fraktale mit großen Farbabstufungen gedruckt. Auch das ist noch nicht die große Kunst.
Wenn Sie
auf das Bild unten klicken, wird eine neue Farbtafel gezeigt. Man muss die Farben von links nach rechts und von oben nach unten
lesen. Somit hat die gezeigte Farbtafel vier mal 800, also 3200 Farben. Farbabstufungen kann man nicht erkennen,
weil mit dem Befehl
lerpColor() stetige Farbübergänge
zwischen zwei Farben erzeugt werden. Wenn Sie eine eigene Farbtafel erzeugen wollen, müssen Sie drei Entscheidungen
treffen:
Wieviele Farben soll die Tafel enthalten?
Welche "Ankerfarben" sollen gewählt werden?
Wieviele Zwischenfarben zwischen zwei Ankerfarben soll es geben?
In der vom Sketch farbVerlaeufe erzeugten Farbtafel
(Bild unten) ist der Ort der Ankerfarben durch weiße senkrechte Striche markiert. Man kann diese zentralen Farben
entweder explizit angeben, durch Zufall bestimmen oder mit einem wie auch immer gearteten Algorithmus errechnen lassen.
Schauen Sie sich den Sketch an! Dort finden Sie viele verschiedenen Methoden in der Klasse FarbTafel.
Beispiel 1: Viele Fixpunkte als starke Attraktoren
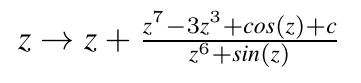
Auf den ersten Blick könnte man meinen, dass die Iteration links wieder aus der Nullstellenberechnung einer Funktion f
entstanden ist. Da der Nenner jedoch nicht die Ableitung des Zählers ist, haben wir es hier mit einer ganz anderen
Iteration zu tun. Bedenken Sie auch, dass Sinus und Cosinus auf der Menge der komplexen Zahlen nicht beschränkt sind.
Der Betrag der Funktionen wächst mit dem imaginären Anteil sogar exponentiell! Einen ersten Überblick über die
Besonderheiten dieser doch recht komplizierten Iteration bekommt man, indem man zunächst einen größeren Ausschnitt
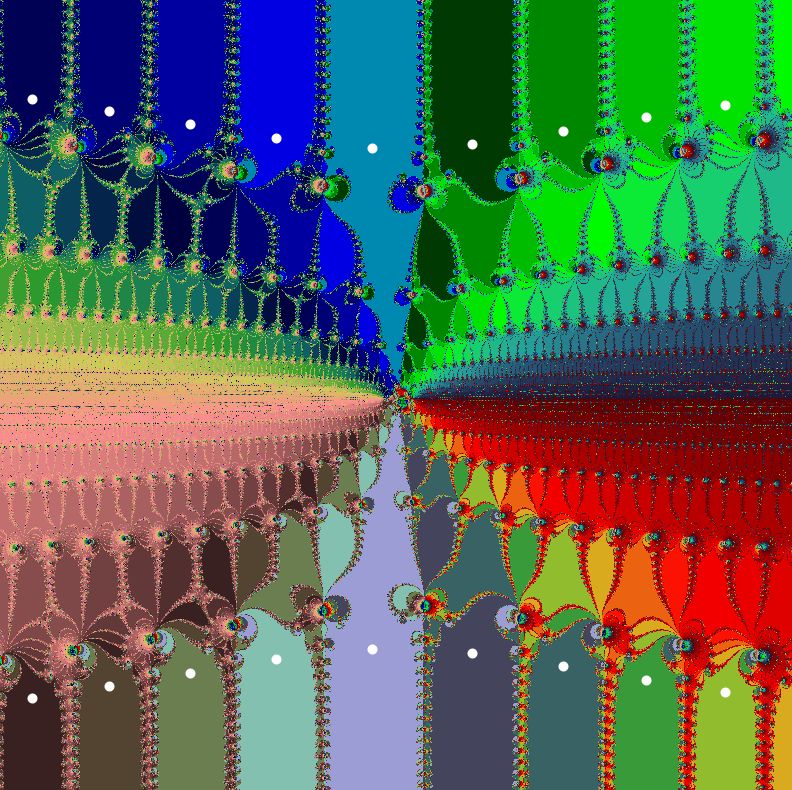
kontrolliert (hier im Realteil wie Imaginärteil von -36 bis 36). Die Zuordnung der Farben geschah beim folgenden
Bild durch den Winkel des n-ten Folgengliedes. Das funktioniert deshalb hier recht gut, weil es viele Fixpunkte
gibt (weiß), die starke Attraktoren sind. Dadurch werden auch die verschiedenen Fatou-Gebiete deutlich sichtbar.
Die verwendete Farbtafel im zugehörigen Sketch juliaBeispiel1
konstruiert elegante Farbübergänge, ohne dabei zu bunt zu sein. In der Gegend des Ursprungs (in der Mitte des obigen
Bildes) scheint es etwas hektischer zuzugehen (unten Bild 1).
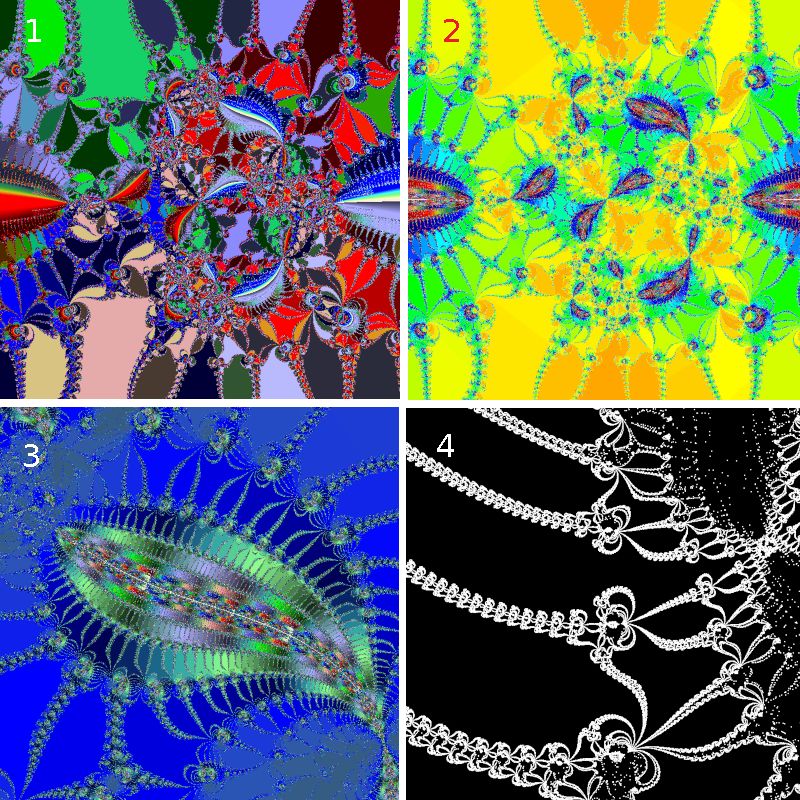
Weniger bunt wird das Bild durch die Verwendung ähnlicher "Ankerfarben".
In Bild 2 (gleicher Bildausschnitt wie in Bild 1) kommt nicht nur eine andere Farbtafel zum Einsatz,
die einzelnen Farben sind auch ganz anders zugeordnet. Es handelt sich hier um ein "Fluchtgeschwindigkeits-Bild".
Während in 1 die Winkel des n-ten Folgengliedes die Farbe bestimmen und damit haupsächlich die Fatou-Gebiete
herausheben, ist es in 2 die Entfernungen des n-ten Folgengliedes.
Bild 3 ist eine vergrößerter Ausschnitt aus Bild 2 mit einer anderen Farbtafel. So entsteht der Eindruck eines in Wasser
schwimmenden Pantoffeltierchens.
Bild 4 zeigt in weiß auf schwarz den ungefähren Ort der Julia-Menge an. (Siehe letztes Kapitel)
Beispiel 2: Viele Fixpunkte als schwache Attraktoren
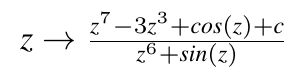
Die verwendete Farbtafel ist im Idealfall für die aktuelle Iteration maßgeschneidert. In diesem Beispiel, das sich vom
vorherigen nur durch das Fehlen eines Summanden z unterscheidet, sind die Attraktoren nur ganz schwach anziehend.
Mit anderen
Worten, um einen Orbit zu zeichnen, der seinem Fixpunkt beliebig nahe kommt, müssen eventuell hunderttausend Iterationen
vorgenommen werden. Der Ausschnitt unten zeigt den Bereich für x und y zwischen -3 und 3. Die Farben wurden
entsprechend der "Konvergenzgeschwindigkeit" zugeordnet, wobei berücksichtigt wurde, dass sich die Werte in einer
Iteration nur minimal ändern. (Fixpunkte gibt es in diesem Ausschnitt nicht.)

Im nächsten Bild links oben (1) wird wie in Beispiel 1 der Ausschnitt von -36 bis 36 in x und y dargestellt.
Die Farben werden dem Winkel des letzten Folgengliedes zum Ursprung zugeordnet. Neben den
Fixpunkten sind 500 Orbits bis zum Element z100000 eingetragen (weiß).
Man sieht hier sehr schön die verschiedenen Fatou-Gebiete mit ihrer fraktalen Struktur.

Bild 2 ist eine starke Vergrößerung mit Farbkodierung per Konvergenzgeschwindigkeit. In Bild 3 sind wieder
Fatou-Gebiete erkennbar. Zusätzlich wurde einige "Fallen" aufgestellt. (Mehr dazu im nächsten Kapitel "Traps").
Bild 4 zeigt einen Ausschnitt aus der Julia-Menge. Experimentieren Sie doch selbst mit dieser Iteration.
Der ausführlich kommentierte Sketch juliaBeispiel2
kann hier runtergeladen werden.
Beispiel 3: Zyklische Fixpunkte als starke Attraktoren
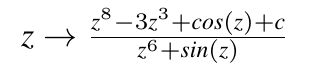
Beispiel 3 unterscheidet sich vom letzten Beispiel lediglich im ersten Summanden des Zählers: z8
statt z7. Die weißen Punkte im Bild unten (x und y im Bereich -36 und 36) sind sieben von tatsächlich
neun vorhandenen zyklischen Fixpunkte. Die beiden fehlenden Fixpunkte befinden sich außerhalb des Bildausschnitts.
"Zyklisch" bedeutet, dass die einzelnen Fixpunkte nach jedem neunten Iterationsschritt angelaufen werden.

Es gibt hier daher nur zwei verschiedene Fatou-Gebiete (Bild unten. Attraktor "unendlich": schwarz).
Da die Folge nach n Schritten, falls sie nicht divergiert, bei einem der neun zyklischen Attraktoren stehen bleibt,
benötigt man bei der Zuordnung der Farbe mit dem Ursprungswinkel-Verfahren nur genau 10 Farben.
(Siehe folgendes Bild mit x- und y- Ausschnitt zwischen -7,2 und 7,2)

Der gleiche Ausschnitt- aber nur schwarz-weiß (schwarz für Divergenz und weiß für Konvergenz):

Nachfolgend wieder gleicher Ausschnitt, wobei mit dem
BSM-Verfahren
die Julia-Menge markiert wird:

Die nächsten zwei Bilder zeigen ein Bildausschnitt für x und y zwischen -2 und 2. Das erste Bild wurde mit dem
Konvergenz-Geschwindigkeits-Verfahren und das zweite Bild mit dem Ursprungswinkel-Verfahren eingefärbt.
Achten Sie darauf, dass im unteren Bild aus dem gerade dargelegten Grund keine Farbübergänge möglich sind.


Es gibt unzählige Möglichkeiten, eine Farbtafel mit der oben dargestellten Methode zu erstellen. Wer sehr
viele verschiedene Tafeln benötigt, tut gut daran, nicht nur eine Klasse FarbTafel zu erstellen. Die
Klasse wird dann schnell unübersichtlich. Weiter unten kann man daher drei verschieden FarbTafel-Klassen
runterladen. Alle drei sind in einer kleinen Anwendung untergebracht, mit Hilfe derer man die Tafeln auch
anschauen kann. Die drei Klassen heißen FarbTafelTrap, FarbTafel1024 und FarbTafel8192.
Die erste Klasse eignet sich besonders für "Traps" (siehe nächstes Kapitel - Beispiel im Bild unten)
, die zweite stellt zahlreiche
Farbtafeln zur Verfügung, die aus 1024 Farben bestehen. Die dritte schließlich ist für den Fall gedacht, dass
man sehr viele Farben im Farbverlauf benötigt. Wie der Name schon sagt, sind es hier bis zu 8192 Farben, auf
die man zugreifen kann.

juliaBeispiel1 juliaBeispiel2 juliaBeispiel3
Menu