Bilderfallen in Juliafraktalen
 Im Themenbereich Fraktale haben wir auch "Fallen" (traps) untersucht. Diese Fallen waren entweder Kreisflächen oder sie wurden
durch zwei parallele Geraden begrenzt. Die Art der Färbung sorgte dafür, dass eine Art 3D-Effekt entstand.
Man kann natürlich ebenso gut Bilder zur Definition der Fallen verwenden. Stellen Sie sich vor, auf einem schwarzen
Hintergrund sind, wie beim Bild links, kleine Teile eines oder mehrer Fotos platziert. Landet eine Iteration auf einem
dieser Bilder, wird die Iteration - wie bei Fallen üblich - gestoppt. Der Ausgangspunkt bekommt dann den dort
gefundenen Farbwert. Wichtig ist dabei, dass der Hintergrund außerhalb genau color(0) ist. Ist dies der Fall,
kann die Iteration weiter laufen - es sei denn, es ist bereits die maximale Anzahl der Iterationen erreicht.
Bei komprimierten Bildformaten, wie jpg oder png, kann diese Eigenschaft verloren gehen. Wir verwenden daher das
nicht komprimierte bmp-Format. Außerdem verwenden wir für die Färbung des Julia-Fraktals die
Winkel- und Streckensumme Methode.
Im Themenbereich Fraktale haben wir auch "Fallen" (traps) untersucht. Diese Fallen waren entweder Kreisflächen oder sie wurden
durch zwei parallele Geraden begrenzt. Die Art der Färbung sorgte dafür, dass eine Art 3D-Effekt entstand.
Man kann natürlich ebenso gut Bilder zur Definition der Fallen verwenden. Stellen Sie sich vor, auf einem schwarzen
Hintergrund sind, wie beim Bild links, kleine Teile eines oder mehrer Fotos platziert. Landet eine Iteration auf einem
dieser Bilder, wird die Iteration - wie bei Fallen üblich - gestoppt. Der Ausgangspunkt bekommt dann den dort
gefundenen Farbwert. Wichtig ist dabei, dass der Hintergrund außerhalb genau color(0) ist. Ist dies der Fall,
kann die Iteration weiter laufen - es sei denn, es ist bereits die maximale Anzahl der Iterationen erreicht.
Bei komprimierten Bildformaten, wie jpg oder png, kann diese Eigenschaft verloren gehen. Wir verwenden daher das
nicht komprimierte bmp-Format. Außerdem verwenden wir für die Färbung des Julia-Fraktals die
Winkel- und Streckensumme Methode.
Entscheidend für die Berechnung von Fraktalen ist die Beziehung zwischen Pixeln des Bildschirms und den komplexen
Zahlen in der Iteration. Das ändert sich auch hier nicht. Allerdings benögigt man hier auch Attribute für das
verwendete Bild, die sich auch bei Zoomvorgängen nicht ändern. Innerhalb der Iteration prüft man, ob der aktuelle Wert
der Iteration im Bild zu liegen kommt. (xUB, yUB) und (xOB, yOB) sind die den Ecken links unten und
rechts oben des Bildschirms zugeordneten komplexen Zahlen xUB + yOB · i und xOB + yOB · i.
Hier wird geprüft, ob der aktuelle Punkt überhaupt im Bildbereich liegt. Ist dies der Fall, dann berechnet man das
zum Punkt gehörige Pixel und setzt das boolsche Attribut innerhalb für diesen Punkt auf true.
Danach muss nur noch festgestellt werden, ob das entsprechende Pixel schwarz ist.
xTrapF = map((float)zNeu.re,(float)xUB,(float)xOB,0,width-1);
yTrapF = map((float)zNeu.im,(float)yUB,(float)yOB,height-1,0);
xTrap = round(xTrapF);
yTrap = round(yTrapF);
innerhalb = true;
}
......................................................
if(innerhalb && bildMatrix[xTrap][yTrap] != color(0)){
trapped = true;
break;
}
zNeu = zAlt2 + c1

zNeu = zAlt2 + c2

zNeu = zAlt2 + c3

zNeu = zAltzAlt + c

Was die Art der Bild-Fallen angeht, sind der Phantasie keine Grenzen gesetzt. Hier einige Beispiele:
zNeu = zAlt3 + c
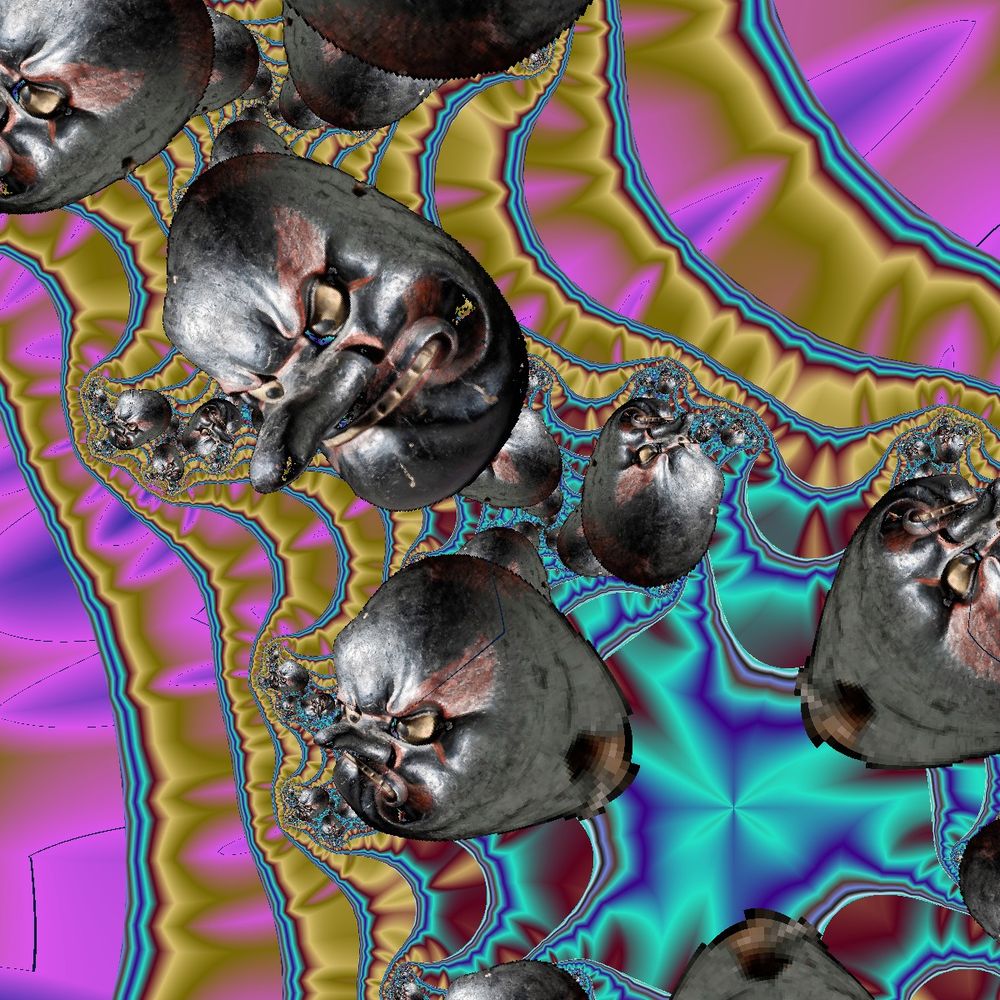
zNeu = zAlt4 + c

zNeu = zAlt8 + c

zNeu = zAlt5 + c
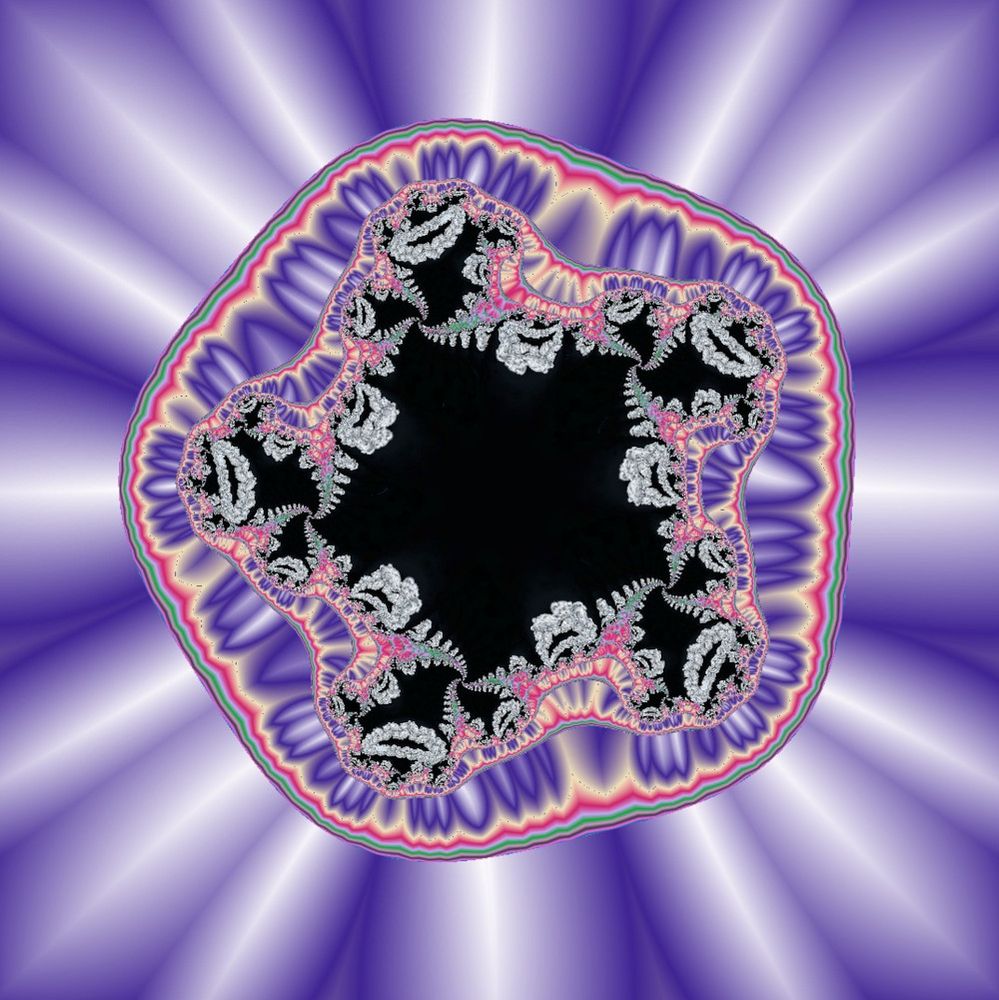
zNeu = zAlt5 + zAlt2 +c
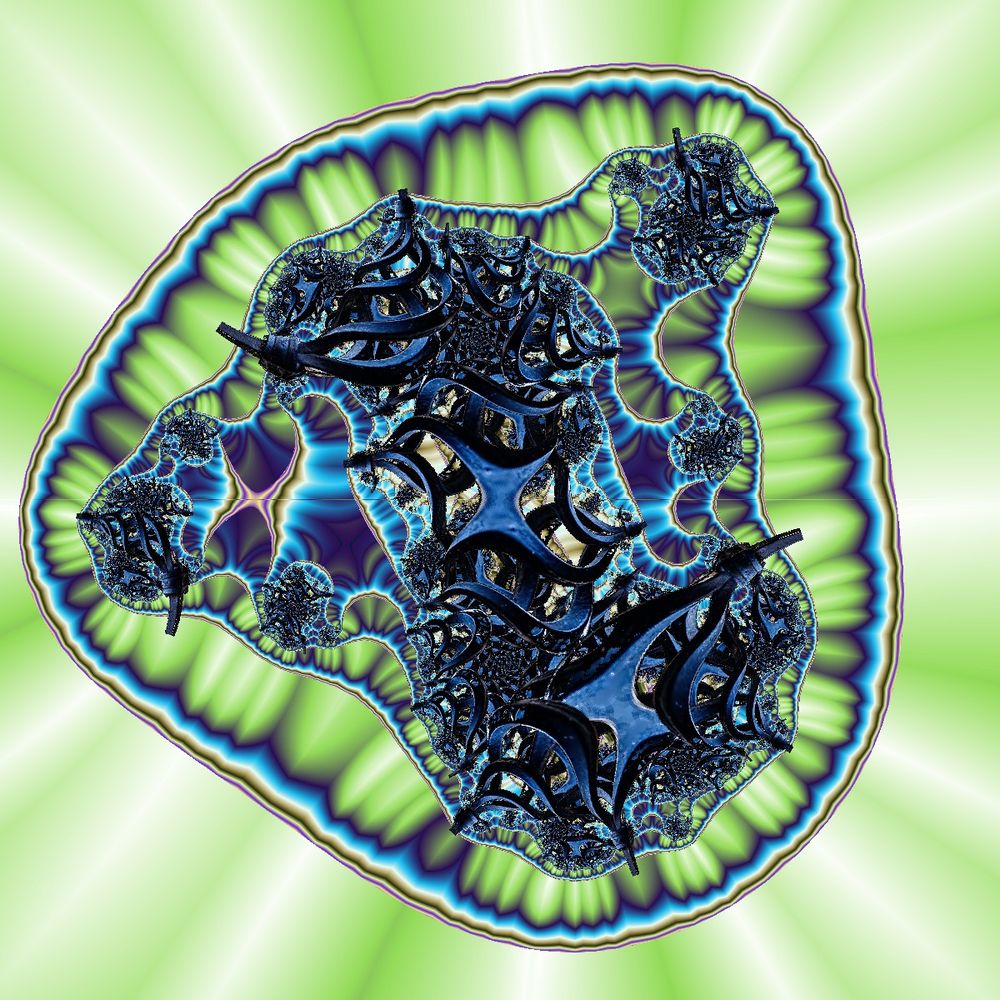
zNeu = zAlt5 + sin(zAlt) + c

zNeu = zAltzAlt + c

zNeu = ezAlt2 + c

Die Sketche können unten heruntergeladen werden. Bei allen Sketchen kann man durch einen Linksklick in das Bild zoomen. Vergessen Sie nicht, vor dem Start ein bmp-Bild in dem Sketchordner abzulegen.
Beachten Sie auch, dass die Anzahl der Threads mit
anzahlThreads = Runtime.getRuntime().availableProcessors()-4;
ausgelesen wird. Dies müssen Sie an die Anzahl der Core in ihrem Prozessor anpassen.
Sketche: Julia Bilderfallen
Menu