Maps
Horseshoe-Map und Cantor-Menge
Die Smalesche "Hufeisen-Abbildung" liefert keine schönen Bilder. Sie ist ein Werkzeug, mit dessen Hilfe man
physikalische Systeme auf chaotisches Verhalten untersuchen kann. Darüber hinaus ist sie äußerst nützlich, wenn
man in anderen Maps, wie zum Beispiel in der Standard-Map
die sehr merkwürdigen hyperbolischen Fixpunkte untersuchen möchte. Im Folgenden Bild wird
auf anschauliche Weise erklärt, wie die Horseshoe-Map und ihre Umkehrung funktioniert.
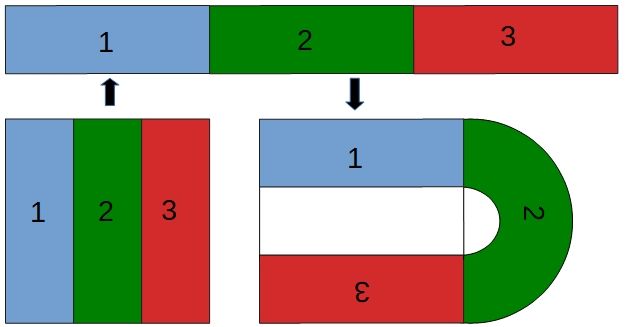
Das Quadrat wird in drei gleichgroße Rechtecke aufgeteilt. Dann wird mit dem Faktor 3 in der senkrechten
Richtung gestaucht und mit dem gleichen Faktor in der waagrechten Richtung gestreckt. Danach biegt man das
Ergebnis zu einem Hufeisen. Die Punkte im grünen Teil sind nicht mehr im Bild vorhanden. Somit ist die Abbildung
nicht bijektiv. Weshalb lässt man das grüne Rechteck nicht einfach weg? Ganz einfach: Dann wäre die Abbildung
nicht mehr differenzierbar!
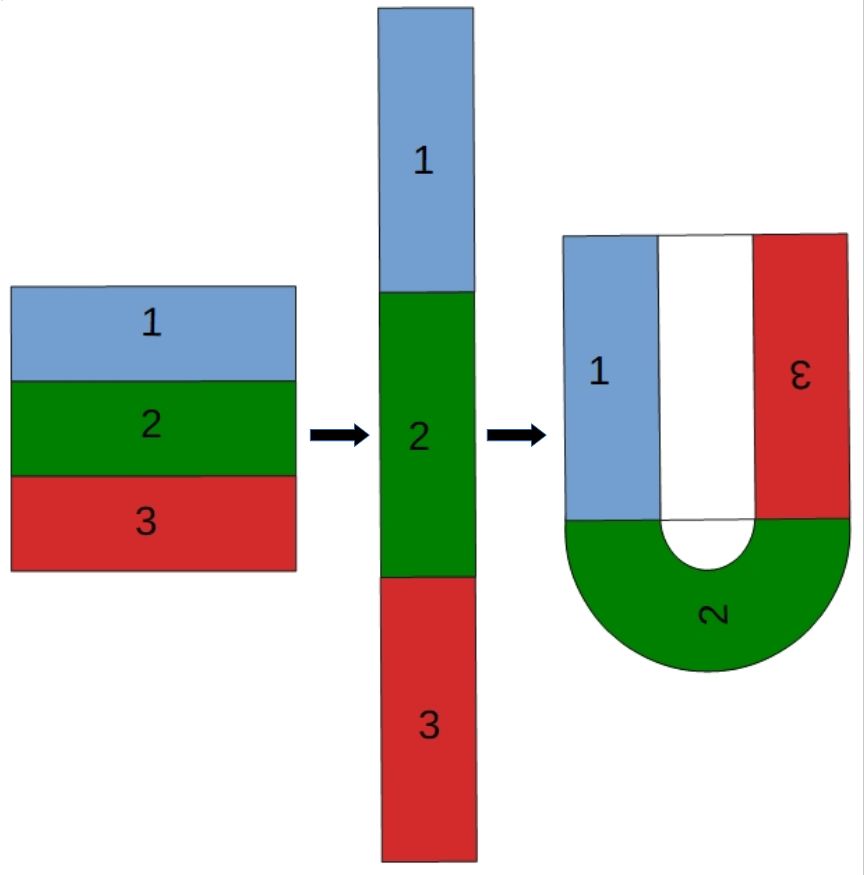
Man kann die Hufeisen-Abbildung umkehren. Wie das geht zeigt das obige Bild. Wieder fallen die Punkte im grünen
Rechteck unter den Tisch. Es wird zuerst waagrecht gestaucht, dann senkrecht gestreckt und schließlich, wie oben,
das Hufeisen geformt. Damit Sie verstehen, dass dies wirklich die Umkehrabbildung ist, versuchen Sie gedanklich
das Ergebnis der Umkehrabbildung erneut abzubilden. Und siehe da, alles sieht so aus, wie zu Beginn. Nur die
Punkte des grünen Rechtecks sind erwartungsgemäß verschwunden.
Im obigen Sketch wurde die Hufeisenabbildung bereits einmal angewendet. Sie können nun durch Klicken der linken
Maustaste jeweils eine weitere Iteration durchführen lassen. Durch Klicken mit der rechten Maustaste wird der
y-Wert mit dem Faktor 2 gezoomt. Auf diese Weise lassen sich bis zu zehn Iterationen durchführen, sofern man
zwischendurch immer wieder die Auflösung der y-Achse vergrößert. Da man beim zoomen mehrer Startpunkte benötigt,
um sauber gezeichnete Rechtecke zu bekommen, dauert der Rechenvorgang etwas länger. Im folgenden Sketch können
Sie die Umkehrung der Abbildung testen:
Die Iterationsformeln können Sie dem Programmcode der Sketche entnehmen. Achten Sie dabei auch auf
eine Besonderheit des Algorithmus: Will man scharf abgegrenzte Rechtecke bei den Iterationen und beim Zoomen
bekommen, muss man viele Millionen Startpunkte wählen. Dann dauert die Rechnung aber sehr lange. Von
daher bedient man sich eines (mathematisch korrekten) Tricks. Wenn bei der Hufeisenabbildung ein y-Wert
errechnet wurde, zeichnet man dort nicht den Bildpunkt, sondern eine waagerechte Linie ein. Denn es gilt:
Wenn beispielsweise der Punkt P(105,432) Bildpunkt ist, dann sind es alle Punkte P(x,432), mit 0 < x < a.
Bei der Umkehrabbildung zeichnet man senkrechte Linien für jeden gefundenen x-Wert.
Stellen Sie sich vor, Sie müssten die Schnittmenge der Bildpunkte der Horseshoe-Map und ihrer Umkehrung bilden.
Der Cantor-Mengen Sketch hat dies bereits erledigt:
Die gelben Punkte dort markieren die Schnittmenge für den Fall, dass man jede Abbildung genau einmal anwendet.
Wie sähe die Schnittmenge aus, wenn man beide Abbildungen zweimal durchführt? Klicken Sie mit der linken Maustaste
auf die Animation und Sie haben das Ergebnis! Nach vier Iterationen werden die kleinen Quadrate ziemlich
ausgefranst. Dann drücken Sie die rechte Maustaste, um in die Ecke oben links mit Faktor zwei zu zoomen. Dieses
Prozedere kann man mehrfach ausführen und somit zehn Iterationen und mehr zu erzeugen.
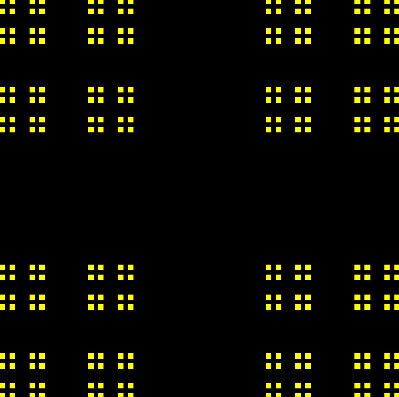
In nebenstehendem Bild sieht man das Ergebnis nach vier Iterationen. Wenn man immer weiteriteriert und nie
damit aufhört, was bleibt dann?
Cantor Staub. (Genauer: Das Kreuzprodukt der
Cantor-Menge mit sich selbst.)
Und dieser Cantor Staub hat es in sich! Zunächst mal hat er ein nichtganzzahlige (Hausdorf-)Dimension, ist
somit ein Fraktal, also auch selbstähnlich.
Das hatten Sie sicher schon vermutet. Dass aber die Menge der Punkte des Cantor Staubs überabzählbar unendlich ist, damit
tut man sich schon deutlich schwerer. Die Menge der reellen Zahlen ist also gleichmächtig wie die Cantor-Menge.
Und nun die merkwürdigste aller Eigenschaften: Das Flächenmaß der Cantor-Menge ist Null! Das können Sie sehr
leicht selbst beweisen. Nehmen wir an, die Seitenlänge des Quadrats und damit auch sein Flächeninhalt sei 1.
Berechnen Sie einfach den Flächeninhalt der schwarzen Fläche, die bei der jeweiligen Iteration
dazu kommt. So kommen Sie auf eine
geometrische Reihe .
Mit den Bezeichnungen der Wikipedia-Seite gilt: a0=5/9 und q =4/9.
Setzt man die beiden Werte in die Formel dort ein, so ergibt sich im Grenzwert ein Flächeninhalt von 1.
Für die Cantor-Menge bleibt also nichts übrig.
Die Punkte in der Cantor-Menge sind, aufgrund der Tatsache, dass sie in allen Schnittenmengen
liegen invariant bezüglich der Horseshoe-Map. Alle anderen Punkte landen ja irgendwann außerhalb des
Quadrats.
Zum Schluss noch eine Bemerkung zur Frage der Bijektivität. Es ist durchaus möglich, die Abbildung so zu verändern, dass sie alle Punkte behält. Man muss dann nur statt des Faktors 3 für Streckung und Stauchung den Faktor 2 verwenden. Dann gibt es keinen "mittleren Bereich" mehr. Diese Art der Abbildung kann dann zum Beispiel an die Cat-Map angeschlossen werden,um noch etwas mehr Chaos im verschlüsselten Bild zu erzeugen...
Horseshoe-Map .Umkehrung der Horseshoe-Map .
Cantor-Menge .
Menu