Maps
Standard Map: Darstellungen
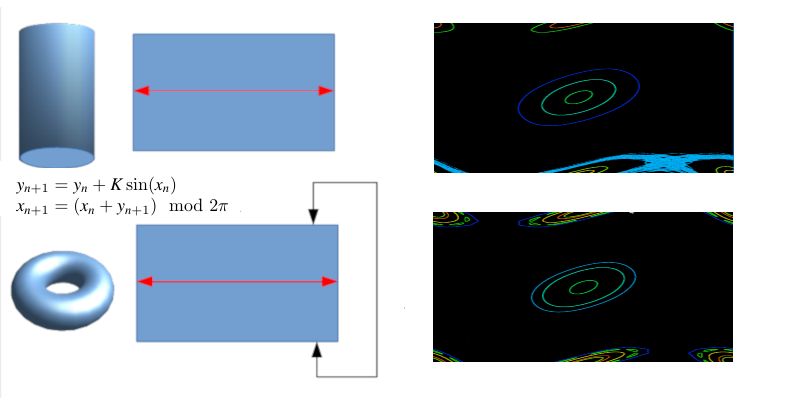
Die Standardabbildung wird erst dann interessant, wenn man mit ihrer Hilfe einen physikalischen Sachverhalt
modellieren kann. Neben dem erwähnten angestoßenen Rotator gibt es unzählige andere physikalische
Gegebenheiten, die sich, möglicherweise mit etwas anderer Interpretation der Variablen, ebenfalls zur
Modellierung mit der Standardabbildung eignen.
Oft erwähnt wird ein auf einer (vertikal, sinusförmig) bewegten Unterlage hüpfender Ball.
Allen gemeinsam ist die Reduktion der Dimension im Poincaré-Schnitt. Im Bild oben ist der Schnitt die Oberfläche
eines Zylinder bzw. ein Torus.
Durch weitere geeignete Schnitte lassen sie sich zu einem Rechteck "aufklappen". Dadurch muss beim Zylinder ein Punkt
auf der linken Seite mit dem Punkt auf der rechten Seite identifiziert werden. Beim Torus ist darüber hinaus
noch die obere und die untere Seite zu identifizieren. (Link zu Sketchen) Durch diese Transformationen bietet
sich nun die Verwendung zweier Variabler x (waagrechte Achse) und y (senkrechte Achse) an. Beim Zylinder ist
y unberschränkt, beim Torus sind beide Variable beschränkt.
Aber auch Elektronen im einer magnetischen Flasche, einem Zyklotron oder Microtron
kann man mit Hilfe Standardabbildung auf Ordnung bzw. Chaos untersuchen. Dort allerdings ist der Querschnitt
kreisförmig, weshalb wir nun die Variablen der Standardabblidung als Polarkoordinaten eines Punktes auf dem
Kreis deuten. Wie Sie sehen werden, ist dies aber nicht der einzige Grund, sich mit dieser dritten Interpretation
zu beschäftigen. Es lassen sich dort manche Zusammenhänge besser erkennen, als mit der aufgeklappten Zylinder oder Torus
Darstellung.
Klicken Sie ins Bild, um eine Trajektorie zu zeichnen, die den angeklickten Punkt enthält. Vergrößern (verkleinern) um Faktor
zwei können Sie durch Drücken der '+'-Taste ('-'-Taste). Man kann mit den Tasten 'r' und
'l' 'den Ausschnitt nach recht bzw. links verschieben.
Nach unten und oben lässt sich der Ausschnitt mit den Tasten 'u' bzw. 'o' verschieben. Damit
lässt sich also jeder beliebige Bereich mit etwas Geduld über 100-fach vergrößern. Mit der Taste 'p' ('m')
vergrößert (verkleinert) man den Störungsfaktor K um 0.05.
Neustart mit Taste 'N'
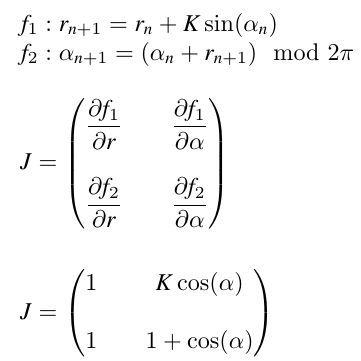Welche Eigenschaften hat die Standardabbildung? Links sehen Sie nochmals ihre Definition bzgl. Polarkoordinaten.
Bei einer differenzierbaren Funktion mit einer Variablen wissen Sie, dass man mit ihrer Ableitung an einer
Stelle x, die Steigung der Tangente an dieser Stelle erhält. So kann man in einer kleinen Umgebung von x die
Funktion durch ihre Tangente ersetzten.
Im Falle der Standardabbildung ist das nicht wesentlich anders. Die links mit J bezeichnete Matrix
heißt Jacobi-Matrix. Die Einträge dort werden durch die "partiellen" Abbleitungen der beiden Funktionen
bestimmt. "Partiell abbleiten" bedeutet, dass man die andere Variable, nach der nicht abgeleitet wird,als Konstante
betrachtet.
(Das Ergebnis steht direkt darunter. So können Sie testen, ob Sie die Methode verstanden haben. Beachten Sie
dabei, dass man für rn+1 in f2 die Definition in f1 verwenden muss!)
Die Rechnung zeigt, dass die Determinante von J (unabhängig von K und α) 1 ist. Das bedeutet
zweierlei: Erstens ist die Funktion umkehrbar (da die Determinate nicht Null ist) und
zweitens ist sie flächen- und orientierungstreu.
Mit Hilfe der Polarkoordinaten Darstellung lässt sich der Beweis des Poincaré-Birkhoff Fixpunkt Theorems
sehr einfach skizzieren. (Ursprünglich wurde das Theorem für das Drei-Körper-Problem benötigt.)
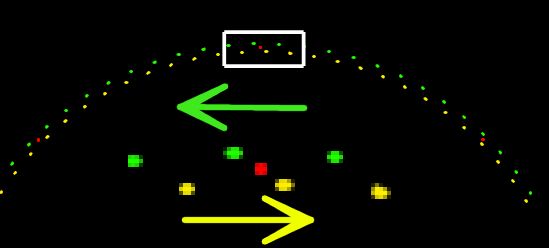
Erinnern Sie sich an die "Rotationszahl"? Man
kann sie hier ganz einfach definieren:
RZ = r/2π, wobei r der Radius der Polarkoordinaten eines
Punktes darstellt. Es gibt, wie Sie sich erinnern, zwei Möglichkeiten: Entweder ist die Rotationszahl rational
oder sie ist irrational. Im Bild oben sehen Sie einen Auschnitt für 1/8 = r/2π (rot) 1/7.9 = r/2π (grün) und
1/8.1 = r/2π (gelb). Der Wert für K ist sehr, sehr klein und beträgt hier K = 0.00001. Es wurden hier 100
Iterationen durchgeführt und trotzdem ist der rote Punkt immer an der gleichen Stelle. Die grünen Punkte hingegen
wandern, wie die Vergrößerung zeigt, nach links (gegen den Uhrzeigersinn), die gelben nach rechts.
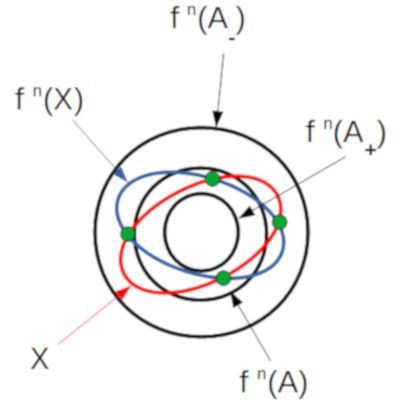Bei so kleinem Wert für K sieht man hier fast perfekte Kreise. Die Punktemenge A im Bild links, bekommt man,
wenn man zu jedem Startwinkel n Iterationen durchführt. In unserem Fall im Bild oben ist n =8 und nur
ein Startwinkel wurde verwendet. Somit bekommt man 8 Punkte eines regelmäßigen Achtecks. (Lässt man mehr als
1000 mal iterieren, dann landen die Punkte irgendwann nicht mehr exakt auf dem vorherigen Punkt, weil die
Rechenungenaugikeit trotz der hier verwendeten double-Attribute zu groß wird.)
Die Mengen A+ und A- stehen für die Rotationzahlen 1/8.1 und 1/7.9. Da der Übergang
der Rotationzahlen von 1/7.9 zu 1/8.1 stetig verläuft, muss es für jeden beliebigen Startwinkel einen Punkt
zwischen fn(A-) und fn(A+) geben,
bei der sich der Winkel unter n-maliger Abbildung nicht verändert. Also fn : (α,r) → (α,r').
Dies gilt für jeden Startwinkel. Die Menge aller Punkte, für die sich bei der Abbildung der Winkel nicht ändert,
sei X (rot). Diese Menge lässt sich ebenfalls mit fn abbilden und man bekommt die Menge fn(X).
Nun ist aber die Standardabbildung, wie wir oben gezeigt haben, f flächenerhaltend,
sodass auch fn flächenerhaltend sein muss.
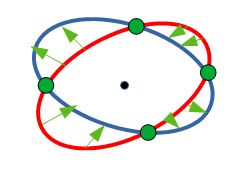Beachten Sie, dass fn auf X rein radial wirkt!
Nun kann man schließen, dass erstens die Schnittpunkte von X und fn(X) Fixpunkte sein müssen
und zweitens, dass es immer ein gerade Anzahl von Fixpunkten geben muss.
Nehmen wir an, ein Fixpunkt sei (α0,r0).
Dann müssen auch f1(α0,r0), f2(α0,r0),...
,fn-1(α0,r0) Fixpunkte sein. Also gibt es für die Ordnung n immer
mindestens n Fixpunkte. Überlegen Sie nun, weshalb es sogar immer mindestens 2n Fixpunkte geben muss!
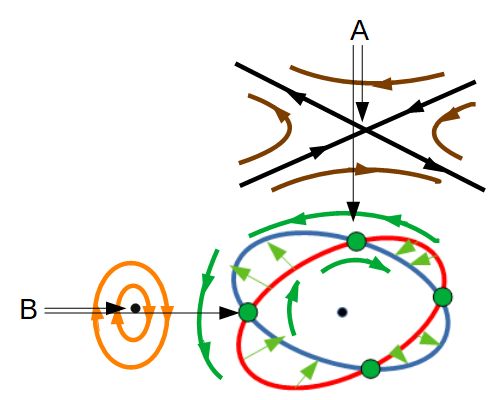Im obigen Bild wurden nun alle bekannten Bewegungsrichtungen der Punkte unter in der einfachen oder mehrfachen Anwendung
der Standardabbildung eingetragen. So kann man deutlich erkennen, dass es mindestens zwei verschiedene Arten
von Fixpunkten geben muss. Punkt A wird hyperbolischer Fixpunkt genannt, Punkt B hingegen
zeigt einen elliptischen Fixpunkt.
Mehr zu diesem Thema finden Sie im Kapitel Fixpunkte
Standard Map Torus .
Standard Map Polarkoordinaten.
Standard Map Torus spezial .
Menu