Maps
Standard Map: KAM- und Can-Torus
Im Sketch unten wurden verschieden Startpunkte, die zu periodischen bzw. quasiperiodischen Bewegungen führen als
Punkt bzw Orbit eingetragen. Es gibt beispielsweise 5 grün gezeichnete Orbits, die in der Mitte einen roten Punkt
besitzen. (Dieser rote Punkt repräsentiert die periodische Schwingung.) Der Nenner der zugehörigen Schwingungszahl
ist daher 5.
Wenn Sie die anderen anderen vier Orbit-Inseln unten zählen, kommen sie auf 8 (rot), 13 (blau) und 21 (gelb) als Nenner. Der Zähler
ist bisher nicht bekannt. Man weiß also beispielsweise noch nicht, ob die Schwingungszahl für die grünen Orbits 1/5, 2/5, 3/5
oder 4/5 ist. Man könnte den Zähler, wie Sie wissen, dadurch bestimmen, dass man kontrolliert, wie oft die Breite 1
durchlaufen wurde, bis der ursprüngliche Orbit wieder erreicht wird. Wären es zum Beispiel 3 mal, dann bekommt man
für den Zähler 3 und für die Schwingungszahl 3/5.
Viel interessanter ist allerdings die Frage, wie man die Orte im Phasendiagramm finden kann, an denen eine
periodische Bewegung vorliegt. Wie Sie im Kapitel Fixpunkte
sehen können, lässt sich das Problem dadurch lösen, dass man zeigt, dass die
Standardabbildung als Hintereinander-Ausführung zweier Involutionen geschrieben werden kann. (Involutionen
sind Abbildungen, die ihre eigene Umkehrabbildung sind, wie zum Beispiel f(x) = -x .) Danach bestimmt man die
Fixpunkte der beiden Involutionen. Diese sind auch gleichzeitig die Fixpunkte der Standardabbildung.
Ein Ergebnis der Rechnung war, dass elliptsche Orbits immer einen Fixpunkt
auf der Geraden x = π haben müssen. (Bei der Normierung auf 1 ist es x = 1/2). Dann kann man mit dem Sketch
Elliptische Fixpunkte bestimmen zugehörigen
y-Werte testen, ob der Punkt (1/2;y) zum Beispiel nach 5 Iterationen wieder sich selbst ergibt. Wenn die Schrittweite
für die y-Werte klein genug ist, bekommt man dadurch einen Startpunkt, der zu allen anderen zugehörigen Fixpunkten
führt. Das Verfahren funktioniert allerdings nur dann zuverlässig, wenn man mit double-Größen arbeitet.
Und so können Sie den Sketch verwenden:
Klick ins Bild: Trajektorie an dieser Stelle
Taste "N": Neustart
Taste "+" und "-": K um 0.01 vergrößern bzw. verkleinern.
Der obige Sketch zeichnet nur für einige besondere Startpunkte die Folgepunkte ein. Hier die
Umgebung dieser Trajektorien und ein letzter KAM-Torus:
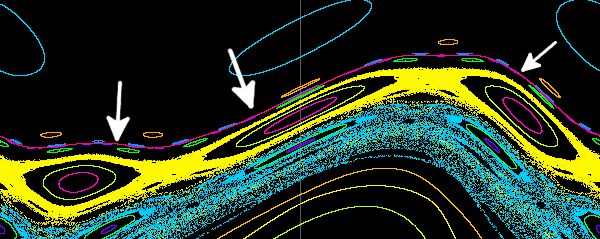

Dieser "letzte" KAM-Torus wird auch goldener KAM-Torus genannt. Man erhält ihn bei K = 0.971635.
Seine Schwingungszahl ist die
"irrationalste Zahl"
, die es gibt, also diejenige, die sich am schlechtesten durch rationale Zahlen approximieren lässt.
Eine solche Approximation bekommt man mit Hilfe der Fibonacci-Zahlen auf folgende Weise:
1/1, 1/2, 2/3, 3/5, 5/8, 8/13, 18/21, ...
(Summe aus Zähler und Nenner des letzte Elements ergibt den neuen Nenner, neuer Zähler ist alter Nenner.)
Die orangen Orbits im Sketch gehören zur Schwingungszahl 3/5, die grünen zu 5/8, die blauen zu 8/13 und
die nur in der Vergrößerung darunter zu sehenden magenta-farbenen zu 18/21.
Nun können Sie versuchen in obigem Sketch den sich gerade auflösenden, letzten KAM-Torus (rot) zu überprüfen.
Natürlich bleibt die rote Linie nicht als Linie erhalten, sofern man nur stark genug vergrößert. Sie können
durchaus versuchen, einen "besseren" Wert für den letzten KAM-Torus zu finden.
Erhöht man
K ein wenig, dann bekommt man eine fraktale Inselkette, die Cantorus genannt wird. Der Cantorus stellt
keine Barriere mehr da für die Trajektorien, ist also durchlässig.
Golden-KAM-Torus .
Elliptische Fixpunkte bestimmen .
Menu