Simulation
Doppelpendel
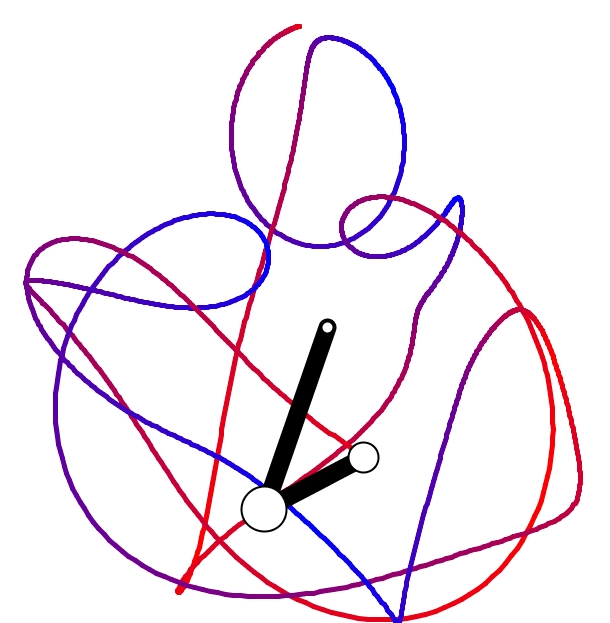
In diesem Sketch wird ein Doppelpendel, auch Chaospendel genannt, simuliert. "Chaos" deswegen, weil man
nicht in der Lage ist, aus einer gegebenen Anfangssituation den Ablauf der Bewegung zu berechnen. Allerkleinste
Abweichungen von der Anfangslage ergeben völlig andere Abläufe der Bewegung. Weil man diesen Sketch leider
nicht mit geringerem Rechenaufwand schreiben kann, sehen die Smartphone-Nutzer die Bewegung möglicherweise zu langsam.
Um den Ablauf später als Ganzes zu sehen, lassen wir den unteren Pendelkörper eine Spur zeichnen.
Das Bild links zeigt einen Screenshot, der nie mehr wieder genau so aussehen wird.
Die Mathematik dahinter ist recht anspruchsvoll. Wenn Sie den Sketch runterladen, sehen Sie eine Methode
"updatePendel". Dort werden die nötigen Differentialgleichungen näherungsweise mit
"Runge-Kutta 4" gelöst.
Man kann den Programmcode
auch dann im Wesentlichen verstehen, wenn man nicht genau weiß, wie die nächste Positionen in besagter Methode
berechnet werden. Die Animation unten können Sie durch Klick in den Raum des Pendels mit neuen Anfangswerten neustarten. Dabei
wird abwechselnd mit und ohne Spur animiert. Weil bei jedem draw()-Durchgang alles gelöscht wird,
müssen die Punkte in einem ListArray gespeichert werden. Das Verlangsamt die Darstellung mit der Zeit immer mehr.
Ein Klick auf das grüne Rechteck unten verlangsamt die Bewegung und führt durch das kleinere Zeitintervall dt zu
genaueren Werten. Ein Klick auf das rote Quadrat lässt das Pendel schnellere Bewegungen ausführen, die aber,
durch das größere Zeitintervall dt zu ungenaueren Werten führt. Für genauere Werte klicken Sie (eventuell mehrfach) auf das grüne
Quadrat.
Hintergrundinformationen zum
Doppelpendel finden Sie bei Wikipedia.

Um zu verstehen, was an dem Verhalten des Doppelpendels chaotisch werden kann, hilft es (wie auch beim Kicked Roatator) ein Phasenbild, wie links dargestellt, zeichnen zu lassen. Die waagrechte Achse gibt den aktuellen Winkel, die senkrechte die aktuelle Winkelgeschwindigkeit an. Die Frage ist nur: Von welchem der beiden Pendelkörper? Wenn wir wirklich nur ein Schaubild erzeugen wollen, das alle wichtigen Informationen enthält, dann bleibt uns nichts anderes übrig, als uns auf einen Pendelkörper zu konzentrieren. Und das geht so: Weil der Vorgang reibungsfrei ablaufen soll, bleibt die Gesamtenergie erhalten. Aus vier Freiheitsgraden werden dann nur noch drei. Um auf die gewünschten zwei Variablen (z. B. Winkel und Winkelgeschwindigkeit des oberen Pendels) zu kommen, vereinbaren wir, dass nur genau dann, wenn der untere Pendelkörper von rechts nach links durch seine Ruhelage läuft, der Zustand des oberen Pendels festgehalten wird. Man erhält dann einen sogenannten "Poincaré-Schnitt" . Wir werden an anderer Stelle darauf zurückkommen.
Wenn Sie sich vorstellen, dass so unglaublich viele Punkte im Bild links eingetragen sind und ein Punkt immer
nur dann entsteht, wenn das untere Pendel von links kommend durch die Ruhelage schwingt, dann ist Ihnen klar,
dass die Animation etliche Stunden gelaufen sein muss...
Sie können das aber selbst testen. Entweder indem Sie sich den Sketch "doppelPendelPhase" herunterladen oder,
sofern in ihrem Browser JavaSkript nicht deaktiviert ist, gleich
hier
zur Tat schreiten.
Sketch doppelPendelPhase.
Menu