3D mit Processing
Analytische Flächen drucken

Bonan-Jeener-Klein Surface
Falls Sie sich in Blender noch nicht auskennen, lesen Sie sich zunächst folgende Seiten durch:
How to Prepare a Model for 3D Printing
Parametrische Flächen drucken
Inzwischen besitzen viele Bastler einen 3D-Drucker. Was liegt näher, als die berechneten Flächen in der Form einer
Datei dem Programm zu übergeben, das damit den Ausdruck vorbereitet. Ein solches Programm nennt man Slicer .
Leider ist die Sache nicht ganz so einfach, denn bisher haben wir keine derartige Datei erzeugen können.
In der Regel erwartet der Slicer eine stl-Datei. Beginnen wir mit einem drucktechnisch einfachen Fall:
Den Sketch dazu finden Sie im Abschnitt
"Parametrische Flächen" .
Wir benötigen hierfür eine Bibliothek:
Wir führen eine boolean-Variable namens "aufzeichnen" ein, die man per geeignetem Tastendruck verändern kann. Dann muss im draw()-Teil folgender Code stehen:
MeshExport obJ = (MeshExport) createGraphics(400,400,"nervoussystem.obj.OBJExport","infos3D.obj");}
obJ.setColor(true);
obJ.beginDraw();
gridZeichnen(obJ);
obJ.endDraw();
obJ.dispose();
aufzeichnen = false;
Nach entsprechendem Tastendruck findet man drei neue Dateien im Sketch-Ordner, wobei hier nur die Datei info3D.obj benötigt wird. Die Auflösung ist hier auf 400x400 eingestellt. Diese können Sie nach Ihren Bedürfnissen anpassen.
Zunächst wollen wir das Ei in eine "3D-druckbare Form" bringen. Mit anderen Worten: Wir müssen eine Mannigfaltigkeit aus den 3D-Daten erzeugen. Ob das gelungen ist, kann man in Blender testen:
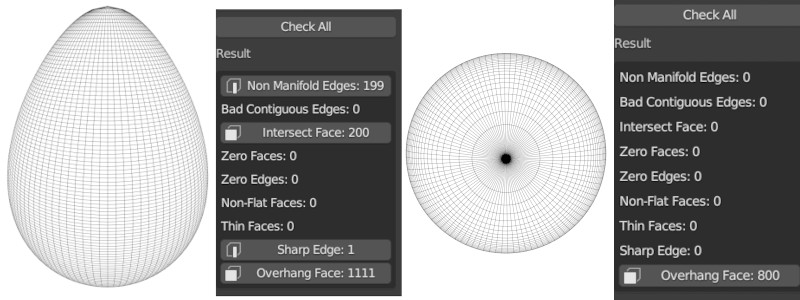
Was soll bei einem solch einfachen Netz schon schiefgehen? Links oben erkennt man, dass Blender keinesfalls zufrieden ist. Rechts daneben sehen wir den Grund: Es gibt ein Loch im Netz oben und unten. Das kann man Blender automatisch reparieren lassen, indem man "Make Manifold" wählt. Danach ist alles so weit in Ordnung, bis auf die überhängenden Flächen. Damit kommen aber die meisten Slicer zurecht. Notfalls werden leicht zu entfernende Stützstrukturen eingefügt.
Bei der ganz oben abgebildeten Bonan-Jeener-Klein Fläche ist die Sache nicht mehr so einfach. Schaut man sich das folgende Bild an, ist klar, woran das liegt:
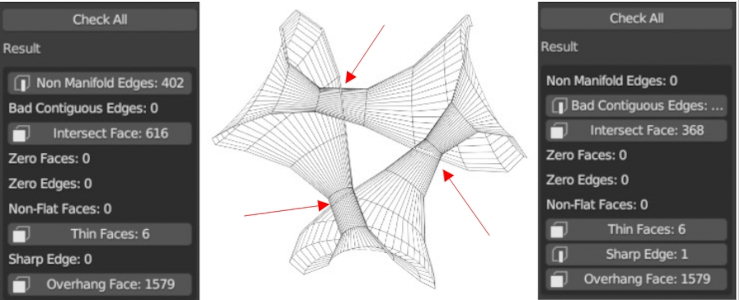
Vor der Bearbeitung mit Blender bekommen wir die Nachricht, dass sich 616 Flächen (hier Vierecke) schneiden. In der Mitte ist die Bonan-Jeener-Klein Fläche in der Mitte durchgeschnitten dargestellt. (Außerdem wurde die Anzahl der Teilflächen, der besseren Übersicht wegen, stark verkleinert.) Die roten Pfeile zeigen die Stelle, an denen sich die Teilflächen durchdringen. Nach der Bearbeitung durch Blender ist die Anzahl der Schnitte zwar verringert, aber immer noch sind es 386 solche Problemstellen. Händisches Löschen derartiger Flächen ist ein Aufwand, der sich nicht lohnt. Denn es entstehen dadurch Lücken. Die drei Fehlermeldungen am Schluss stellt für die meisten Slicer kein Problem dar. "Intersect Face" allerdings bringt viele zum Straucheln. Wie Sie im Bild oben sehen, gelang der 3D-Druck dennoch. Wenn Sie Glück haben, kennt der äußerst mächtige, kostenlose Slicer UltiMaker Cura Ihren 3D-Drucker. Denn dessen automatische Korrektur löst das Problem ohne Mühe.
Implizite Flächen drucken
Links unten sehen Sie die ausgedruckte Trefoil-Fläche, rechts daneben das berechnete Bild für eine etwas
schlankere Variante. Verwendet wurde der Sketch nach Idee 4 im Kapitel
Implizite Flächen, in dem die Bibliothek
toxiclibs verwendet wurde.
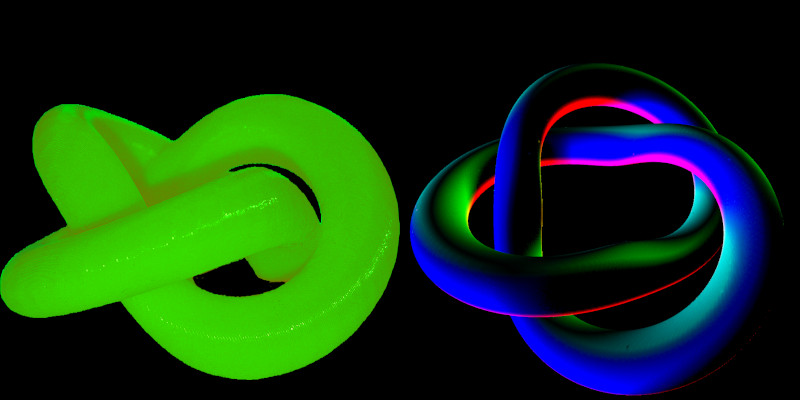
Trefoil Surface
Mit wenigen Zeilen lässt sich eine Triangulierung als stl-Datei erstellen:

gfx.mesh( mesh );
endShape();
mesh.saveAsSTL( sketchPath( "trefoil.stl" ));
Menu