Menu

3D mit Processing

Implizite Flächen

1.Idee

Lesen Sie zunächst auf der Übersichtsseite Analytische Flächen die Definition einer Implizite Flächen durch!
Die gesuchte Fläche ist die Menge der Nullstellen der Funktion f :

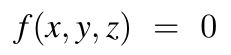
Hier die Nullstellen zu finden, dürfte im Normalfall ein wesentlich größeres Problem darstellen, als bei expliziten und parametrischen Flächen die Punkte auf eben diesen Flächen zu bestimmen.
Das Bild unten zeigt beispielsweise einen Ausschnitt der implizitenFläche bei folgender Nullstellenmenge:


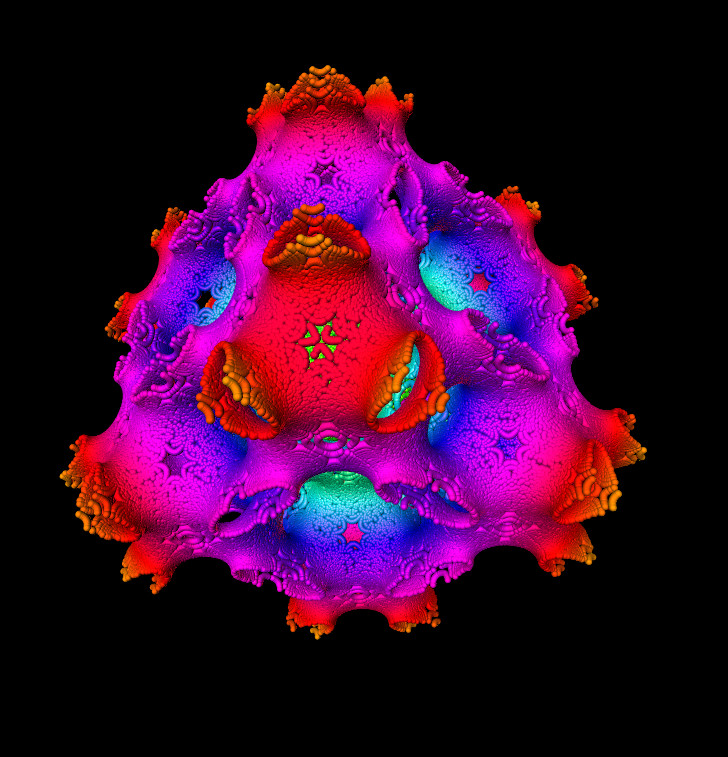
Wie Sie erkennen können, besteht die Fläche aus lauter sehr kleinen Sphären. Das Bild entstand nach einem sehr einfachen, aber äußerst zeitaufwendigen Algorithmus: Man legt in Gedanken ein Gitter über das zu untersuchende Volumen. So entstehen bei gleichem Maßstab lauter Würfel einer bestimmten Kantenlänge. Die Länge der Kanten und die Größe des untersuchten Raumes bestimmen die Rechenzeit. Nun setzt man das Zentrum der Würfel in die Gleichung ein. Dass sich dann exakt Null ergibt, dürfte äußerst selten vorkommen. Daher definiert man einen Grenzwert g. Ergib die Einsetzung des Gitterpunktes einen Fehler betragsmäßig kleiner als g dann wird der Würfel als "Treffer" markiert. Im Bild oben wurden anstatt Würfel kleine Kugeln eingesetzt. Sieht gut aus, ist aber unnötig rechenaufwendig, weil der 3D-Renderer für jede Kugel Licht und Schatten berechnen muss. Gleichgültig ob Würfel oder Kugel, diese kleinen räumlichen Einheiten werden Voxel genannt - zusammengesetzt aus Volumen und Pixel . Eine sehr grobe Voxelpräsentation der obigen Fläche sieht dann zum Beispiel so aus:


Die Schrittweite im Gitter beträgt hier 100 Pixel. Von daher kann man nur eine äußerst grobe Vorstellung der Fläche bekommen. Maximale Auflösung bekommt man mit der Schrittweite ein Pixel. Das Voxel wird dann nur noch durch dieses eine Pixel repräsentiert. Die Farbe wird hier durch den Abstand vom Ursprung bestimmt. Die Voxelstruktur ist nun natürlich nicht mehr sichtbar:



Um die Flächen von allen Seiten anschauen zu können, bietet sich die Methode camera an. Wir richten sie auf den Ursprung aus und bewegen sie auf einer Sphäre mit Radius r. Man benötigt für Positionierung zusätzlich zwei Winkel. Sie kennen das System vermutlich unter dem Namen Polarkoordinaten. So kann die passende Methode aussehen:


In draw rufen wir camera auf und sorgen gleichzeitig für eventuelle direkte Beleuchtung von allen Seiten.


Bleibt der Aufruf unter keyPressed() :


Beachten Sie dabei, dass der Winkel für UP und DOWN nur zwischen -PI/2 und PI/2 liegen darf!
Im folgenden Bild sind vier weitere implizite Flächen abgebildet:



Die Fläche unten links wird Römerfläche oder Steinerfläche genannt. Ihre Gleichung ist:

Oben rechts ist die Boysche Fläche zu sehen. Ihre Gleichung ist ungleich komplizierter: Unten können Sie die fünf hier behandelten Sketche runterladen.

2.Idee

Wenn man wie oben camera und cube benutzt, werden hinter den Kulissen Drehungen durchgeführt und fertige Shapes verwendet. Im folgenden Sketch machen wir alles selbst, ohne rotateX oder ähnliches zu verwenden. Drehungen mit Hilfe von Matrizen und Voxel mit selbst erzeugten Shapes. Dadurch wird das Programm deutlich langsamer, ein Zeichen dafür, wie elegant die fertigen Routinen programmiert sind. Der Vorteil aber, ist, dass man auf diese Weise sozusagen in den "Motorraum" schauen kann. So zum Beispiel kann die Drehung um die x-Achse aussehen:



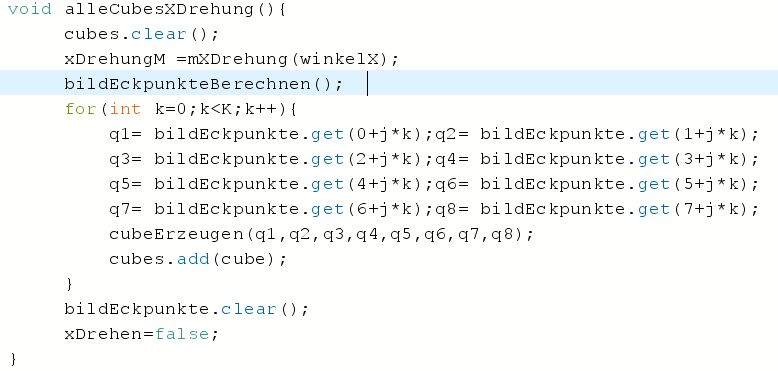
Die benötigte Matrix realisiert man auf folgende Weise:



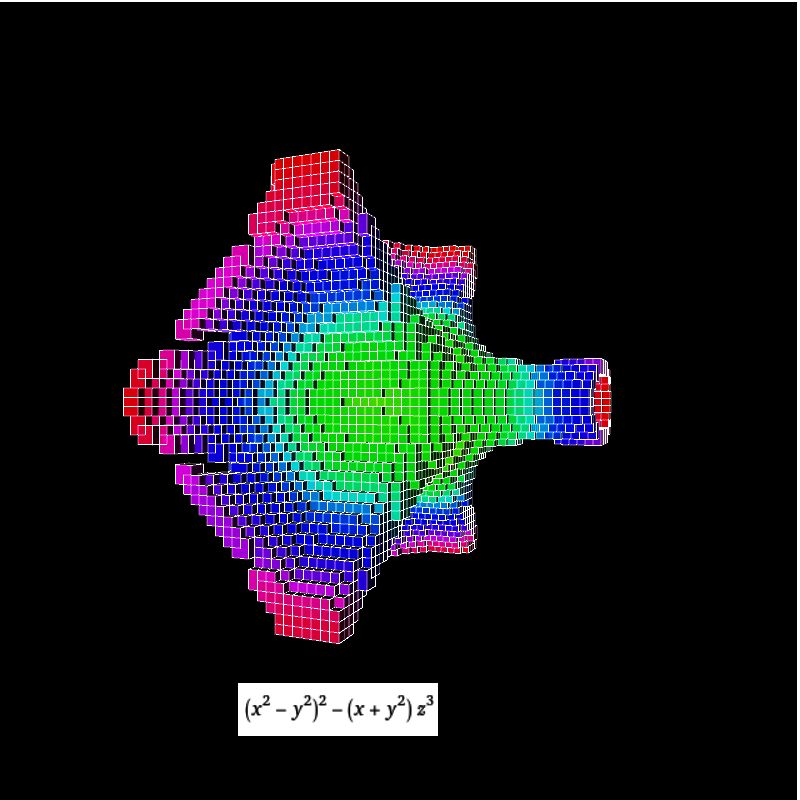
Im folgenden Bild sieht man das Voxelbild, wenn man den dargestellten Term Null setzt. Wenn Sie mit dem unten herunterzuladenden Sketch selbst experimentieren wollen, ist allerdings Geduld gefragt ;-))

3.Idee

Sowohl im Buch als auch hier haben wir das Thema Threads behandelt. Anlass war, dass die heutigen Prozessoren mehrere unabhängig voneinander arbeitende Cores besitzten, so dass man bei geeigneten Sketchen, bestimmte Programmteile auf die verschiedenen Prozessorkerne verteilen kann ("beiläufige Programmierung"). Dieses Kapitel sollten sie zuvor durchlesen.



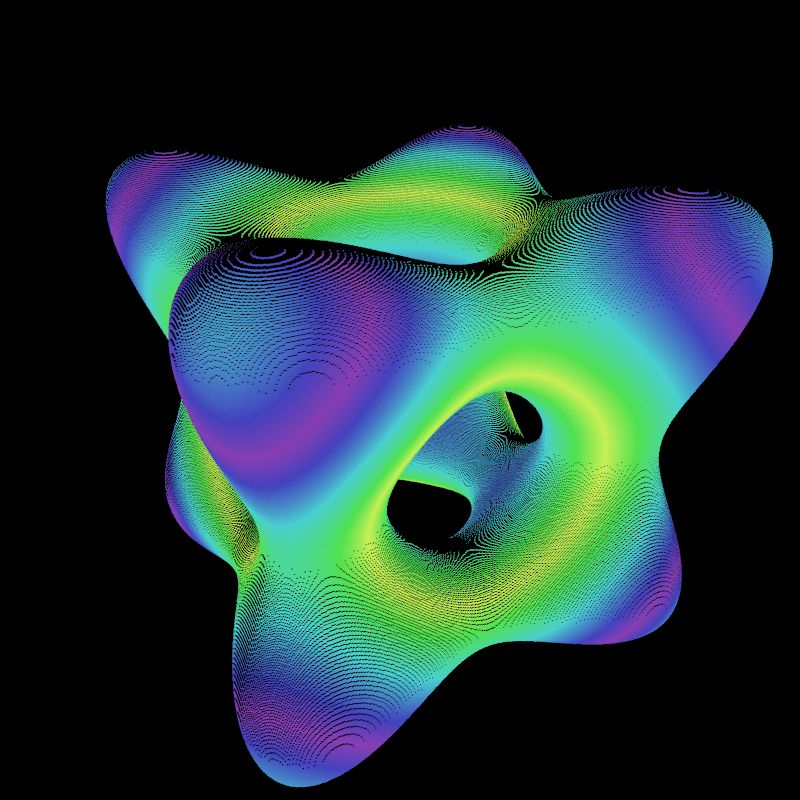
Dem obigen Bild (Tangle Cube) liegt die folgende Gleichung zugrunde:
sq(x)*sq(x)+sq(y)*sq(y)+sq(z)*sq(z) - 5*(sq(x)+sq(y)+sq(z)) +11.8 = 0
Trotz eines sehr engen Prüfgitters (d = 0.01) und einer dadurch einige Millionen starken Treffermenge, benötigt ein PC mit beispielsweise 12 unabhängigen Cores nur wenige Sekunden, bis das Bild entstanden ist. Das liegt hier natürlich auch daran, dass man, wegen der Symetrie der Gleichung, nur ein Achtel des Gitters überprüfen muss.
Und dieses Achtel teilt man in so viele Bereiche ein, wie Cores zur Verfügung stehen. So sieht dann der Programmteil, eine dreifache Schleife, für einen Core aus, sofern man M davon beteiligen will:

Die Methode punktHinzu() befüllt die M ListArrays nach ihrer Nummer n.

Ein weiteres Beispiel ist die Nordstrand's-Weird Fläche. Man muss im Vergleich zu oben lediglich die Gleichung und die Grenzen austauschen:




Interessant ist auch die Banchoff's Chmutov Fläche:



Die zugehörige Gleichung:


Drei Tori, die auf einander senkrecht stehen



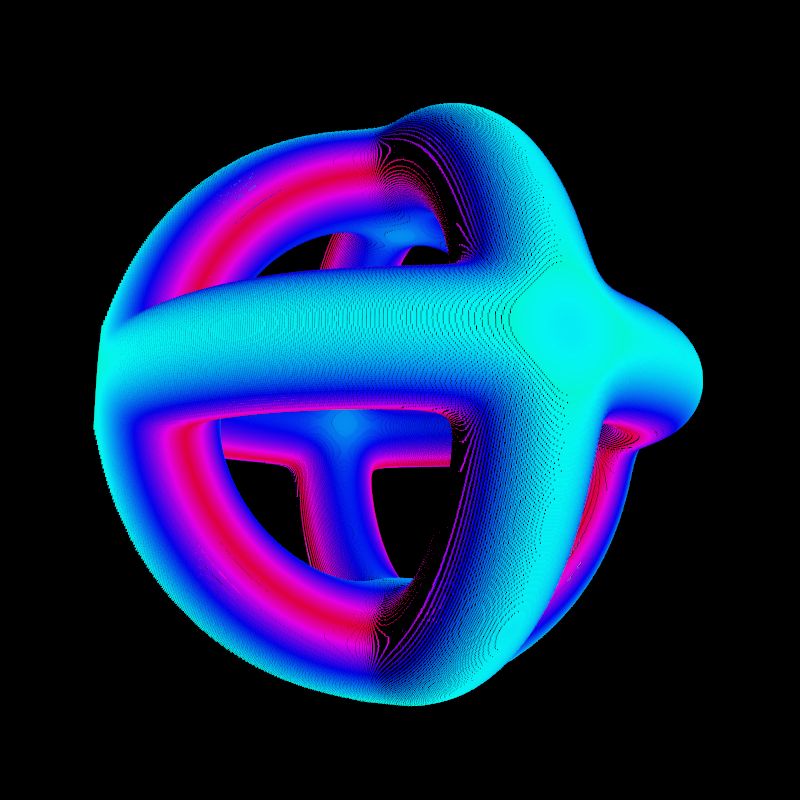
Die zugehörige Gleichung mit den Parametern R und a:



Tangle Cube und Nordstrands Weird



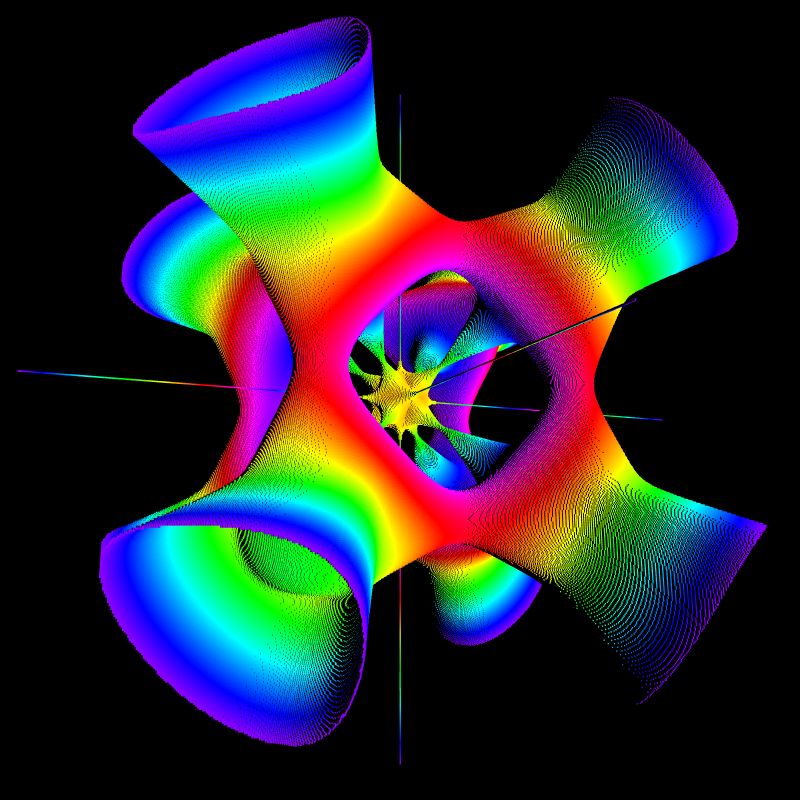
Die zugehörige Gleichung:


Alle fünf Multithreading-Sketche können Sie am Seitenende runterladen.

4.Idee

Im letzten Kapitel des Lehrbuches werden Bibliotheken behandelt. Für unsere Zwecke wären die toxiclibs von Karsten Schmidt hilfreich. Mit ihnen ist es möglich, die Flächen mit der Maus zu drehen und so problemlos von allen Seiten zu betrachten. Die dort verwendbaren Methoden sind hoch effektiv und benötigen daher sogar noch weniger Zeit, als die oben gezeigten Sketche mit Multithreading. Die Flächen werden mit einstellbarer Genauigkeit "triangulisiert". Der Nachteil soll nicht verschwiegen werden: Wer sich nicht die Mühe macht, die Klassen und ihre Methoden in der Dokumentation nachzuvollziehen, versteht oftmals nicht, was genau gerechnet wird. Da dies bereits die vierte Methode ist, derartige Probleme zu behandeln, ist dieser Mangel akzeptabel, zumal man ja die Möglichkeit hat, genauere Informationen in der Dokumentation zu bekommen.
Ein Mittelweg wäre, sich den Marching Cubes Algorithmus , der hier verwendet wird, anzuschauen.



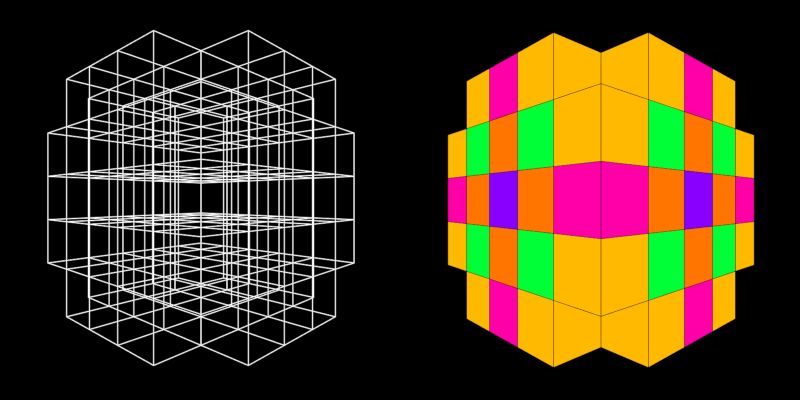
Im Bild oben sehen Sie den schon bekannten Tangle Cube. Links in geringer Auflösung (16 Bit) das aus lauter Dreiecken bestehende Netz. Rechts daneben mit hoher Auflösung (256 Bit) das wesentlich feinere Netz, bei dem die Dreiecke gefärbt worden sind. Mit diesem Sketch ist es möglich, die Flächen durch die bewegte Maus zu drehen. Die Beleuchtung ist so eingestellt, dass die räumliche Struktur besser zu erkennen ist. Die folgenden Bibliotheken benötigt man:

Initialisierungen im setup():


Gezeichnet wird in draw():


Zunächst werden den durchnummerierten Voxeln die Koordinaten x,y und z zugeordnet:


Schließlich muss noch kontrolliert werden, welcher Wert sich ergibt, wenn man x,y und z in die implizite Funktion einsetzt. Das Ergebnis wird in valTest gespeichert. Sollte der Wert kleiner als die vorgegebene Schranke MAX_ISO sein, wird dieser Wert ausgegeben, ansonsten Null.


Hier eine Auswahl erstellter impliziter Flächen:
OL: Banchoff Surface, OR: Barth Sextic, UL: Blob Surface, UR: Boy Surface



OL: Butterfly Surface, OR: Chair, UL: Neovius Surface, UR: No name Surface



Es gibt zwei Methoden, die man in diesem Sketch anwenden kann: Glättung der Fläche durch Lapalace und "voxelize Mesh", was nichts anderes bedeutet, ls dass man das Netz gleichsam mit Legosteinen erzeugt. Bei beiden Methoden geht Information verloren. Außerdem entstehen Lücken, wo sie eigentlich nicht hingehören. Optisch interessant sind solche Gebilde in jedem Fall:


OL: No name Surface, OR: Nordstrand-Weird Surface, UL: Helocoid, UR: Trefoil Surface

Alle zweiundzwanzig zugehörigen Sketche könne Sie unten runterladen.

5.Idee

Vier Methoden zur Bestimmung impliziter Flächen wurden aufgeführt. Weshalb eine 5. Methode?
In einem der folgenden Kapitel soll der "Mandelbulb" behandelt werden. Dort werden wir eine Technik namens "Ray-Tracing" kennenlernen. Um diese Idee vorzubereiten, besprechen wir etwas ganz ähnliches zur Untersuchung bestimmter impliziter Flächen, das hier "Mesh-Tracing" genannt werden soll. Dabei benötigen wir P3D überhaupt nicht mehr. Bedenken Sie dabei: Auch in den vier vorhergehenden Methoden ist das Ergebnis jedes Mal ein zweidimensionales Bild. Bleiben wir doch einfach in zwei Dimensionen! 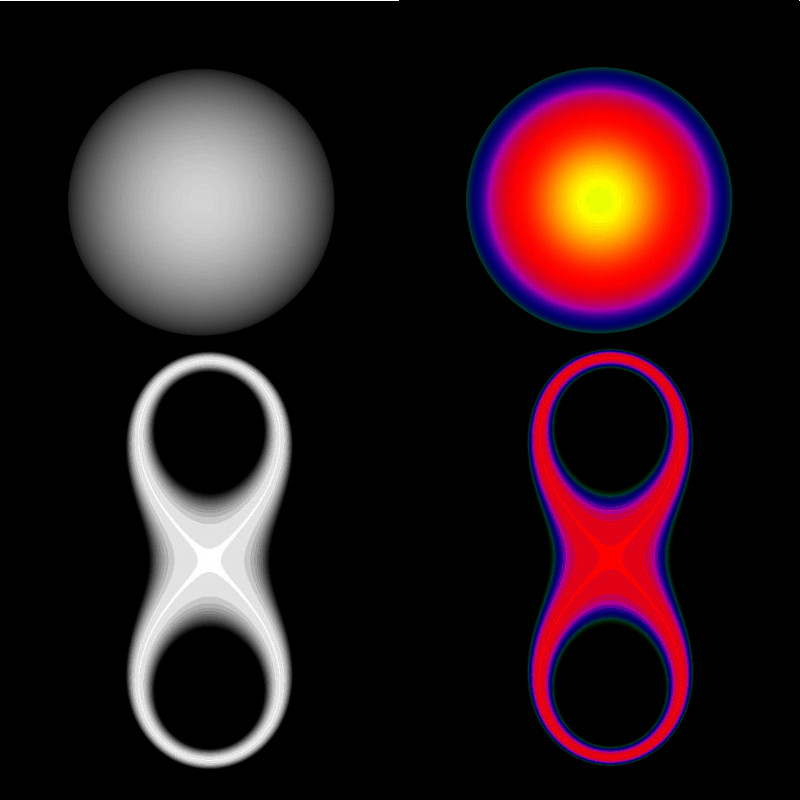Der Sketch unten gibt eine erste Idee: Die zu untersuchende analytische Fläche ist hier eine Kugeloberfläche. Eine Fläche, die in einem bestimmten Abstand zur Kugel aufgestellt ist, denken wir uns ein enges Netz (mesh!) von Punkten. Jeder Punkt auf der Fläche entspricht einem Pixel. Die Fläche ist in alle Richtungen drehbar, was hier als Rotation um die y-Achse dargestellt wird. Somit kann man die Kugel von allen Seiten betrachten. Von jedem Pixel geht nun ein Strahl (ray) senkrecht von der Fläche aus Richtung Gegenstand (Kugel). Auf diesen Strahlen läuft man in kleinen Schritten vorwärts. Die Anzahl der Schritte bis zum Gegenstand wird als Farbe des Pixels codiert. Eine zweite Möglichkeit wäre, die Farbe nach dem Abstand zum Ursprung zu wählen.
Da der Rechenaufwand bei kleiner Schrittweite auf den Strahlen sehr hoch ist, übergeben wir Teilflächen an die einzelnen Core. Die Drehung der Projektionsfläche wird durch Matrizen erzeugt. Wichtig dabei ist, dass man dann den neuen Einheitsnormalen-Vektor (EVN) bestimmt, in dessen Richtung die Punkte auf dem Strahl laufen werden.
Man lässt nun eine Doppelschleife über die Pixel der Projektionsfläche laufen und schreitet auf jedem Strahl so lange vorwärts, bis der Punkt, eingesetzt in die implizite Gleichung einen vorher festgelegten kleinen Wert ergibt. Die Schritte werden gezählt und deren Anzahl bestimmt einen Farb- bzw Grauwert.
So könnten die Schleifen implementiert werden:

Wenden wir unsere Erkenntnisse auf eine hier noch nicht behandelte implizite Fläche an:


Es handelt sich hierbei um einen "Doppeltorus". Das folgende Bild zeigt beide Ergebnisse.




Sketche implizite Flächen (Voxel)

Sketche implizite Flächen (Matrixdrehungen)

Sketche implizite Flächen Multithreading

Sketche implizite Flächen mit Toxiclibs

Sketche implizite Flächen mit Mesh-Tracing

Menu