Menu

3D mit Processing

Parametrische Flächen

Lesen Sie zunächst auf der Übersichtsseite Analytische Flächen die Definition einer Parametrischen Fläche durch! Die Funktion f (siehe unten) wird drei Funktionen erzeugt. Im Gegensatz zu den expliziten Flächen, können hier geschlossene Flächen dargestellt werden.

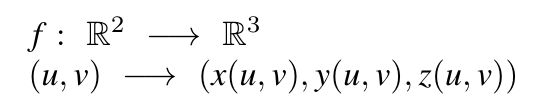
Die Funktion f besteht aus drei verschiedenen Funktionen. Diese ordnen jeder Koordinaten des Raumes per eigener Funktion auf der ebenen Definitionsmenge je einen Wert zu: x = x(u,v), y = y(u,v) und z = z(u,v) zu. Eine parametrische Fläche kann man sich anschaulich so vorstellen:


Unser Ziel ist es, wie bei den expliziten Flächen erwähnt, alle analytischen Flächen mit der Maus "anzufassen", um sie von allen Seiten betrachten zu können.

Die Drehungen um die x- und y-Achse werden daher von der Position der Maus bestimmt. Die Dreheung um die z-Achse bekommt einen festen Winkel, den man aber mit Hilfe der Pfeiltasten vergrößern bzw. verkleinern kann.
Um die Raumpunkte zu berechnen, benutzt man eine doppelte Schleife, die über alle Gitterpunkte läuft. Die x- und y-Werte muss man noch durch den map-Befehl anpassen. Da man den Abstand des Gitterpunktes vom Ursprung für die Farbgebung gut gebrauchen kann, wird der Wert hier in r gespeichert. Unter switch legen wir die Gegebenheiten für die z-Werte ab. Im nachfolgenden Sketch haben Sie neun Wahlmöglichkeiten.

Wie die Shape(QUAD_STRIP) bzw Shape(TRIANGLE_STRIP) gezeichnet werden, entnehmen Sie dem Kapitel Explizite Flächen.
Hier können Sie vierzehn parametrische Flächen erzeugen:

Narushin-Eier

Tasten- oder Mausaktion	Wirkung
Taste w	nächste Fläche
Taste x	Drehung x-Achse start/stopp
Taste y	Drehung y-Achse start/stopp
Taste z	Drehung z-Achse start/stopp
Tasten g	Gitterlinien anzeigen
Tasten +	zoom in
Taste s	Hintergrund schwarz/weiß
Taste a	Anzahl der Gitterpunkte erhöhen
Taste A	Anzahl der Gitterpunkte verringern
Taste t	Teilfläche
Taste f	Farbgebung verändern
in das Bild klicken	zoom out

Wenn man ins Bild zoomt, können die Tasten eventuell verdeckt werden. Mit der Option "in das Bild klicken" können die Tasten wieder sichtbar gemacht werden.

Bemerkung zur letzten (14.) Fläche:
Sie ist ein Spezialfall der "allgemeine Eierformel" von Valeriy Narushin. Am Ende dieser Seite finden Sie weitere Erläuterungen zu dieser Fläche. Zu den Eiern

In diesem auf der html-Seite in JavaScript verwandelten Sketch funktioniert directionalLight leider nicht. Daher sind die räumlichen Effekte nur eingeschränkt zu sehen. In der unten runterzuladenen Version wird der Befehl aber benutzt. Wie er sich auf das Ergebnis auswirkt und welche Funktion benutzt wurde, zeigen die folgenden Screenshots.

Funktion 0: Jeener-Klein Taste: '0'

T = 0.75*cos(3*x+PI/4)+1;
Tx = 3*(2*cos(x)+cos(2*x)-T*sin(x/2)*cos(y));
Ty = 3*a*T*sin(y);
Tz = 3*(2*sin(x)-sin(2*x)-T*cos(x/2)*cos(y));
punkte[ix][iy].x = Tx;
punkte[ix][iy].y = Ty;
punkte[ix][iy].z = Tz;

//Die folgenden Zeilen dienen der Farbgebung. Sie sind für alle folgenden Flächen gleich.

r3D = sqrt(sq(Tx)+ sq(Ty)+sq(Tz));
if(r3D>r3DMax) r3DMax = r3D;//Radius im Raum
if(r3D<r3DMin) r3DMin = r3D;
radius[ix][iy]=sqrt(sq(Tx)+ sq(Ty));//Abstand vom Ursprung in der Ebene
r= radius[ix][iy];
if(r>rMax) rMax = r;//maximaler Radius in der x-y-Ebene
if(r < rMin) rMin = r;
if(Tz > rMax) zMin = Tz;
if(Tz > zMax) zMax = Tz;//für eine Färbungsvariante

Funktion 1: Sphäre, Taste: '1'

Tx = a*8*cos(x)*sin(y);
Ty = 8*sin(x)*sin(y);
Tz = 8*cos(y);

Funktion 2: Clover Knot (Trefoil), Taste: '2'

T=2+0.6*cos(x/2);
Tx = 3*(T*cos(x/3)+0.6*cos(x/3)*cos(y-PI));
Ty = 3*(T*sin(x/3)+0.6*sin(x/3)*cos(y-PI));
Tz = 3*(0.6+sin(x/2)+0.6*a*sin(y-PI));

Funktion 3: Cross Cap, Taste: '3'

Tx = 8*cos(x)*sin(2*y);
Ty = 8*sin(x)*sin(2*y);
Tz = 8*(sq(cos(y))-a*sq(cos(x))*sq(sin(y)));


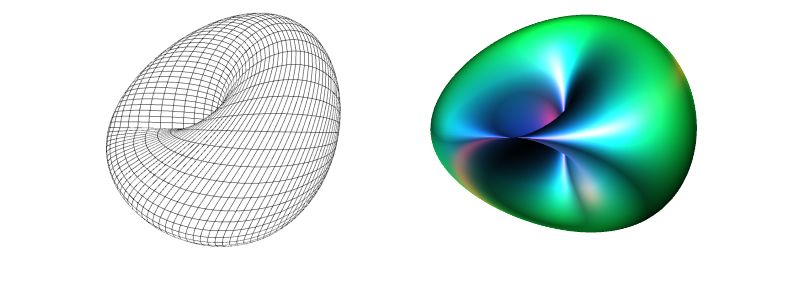
Funktion 4: Immersion der kleinschen Flasche, Taste: '4'

Tx =1.5*(2+3*(cos(x/2)*sin(y)-sin(x/2)*sin(2*y)))*cos(x) ;
Ty =1.5*(2+3*(cos(x/2)*sin(y)-sin(x/2)*sin(2*y)))*sin(x) ;
Tz =1.5*3*a*(sin(x/2)*sin(y)+cos(x/2)*sin(2*y));


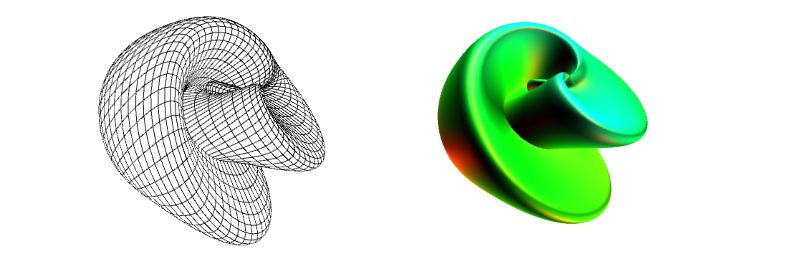
Funktion 5: Immersion der kleinschen Flasche, Taste: '5'

u2=sq(cos(x));u3=u2*cos(x);
u4=sq(u2);u5=u4*cos(x);
u6=u5*cos(x);u7=u6*cos(x);
T1= 3*cos(y)-30*sin(x)+90*u4*sin(x);
T2= 60*u6*sin(x)+5*cos(x)*cos(y)*sin(x);
T3=3*cos(y)-3*u2*cos(y)-48*u4*cos(y)+48*u6*cos(y);
T4=60*sin(x)+5*cos(x)*cos(y)*sin(x)-5*u3*cos(y)*sin(x);
T5=80*u5*cos(y)*sin(x)+80*u7*cos(y)*sin(x);
Tx =-0.64*cos(x)*(T1-T2);
Ty =-10-0.28*sin(x)*(T3-T4-T5);
Tz =0.64*a*(3+5*cos(x)*sin(x))*sin(y);


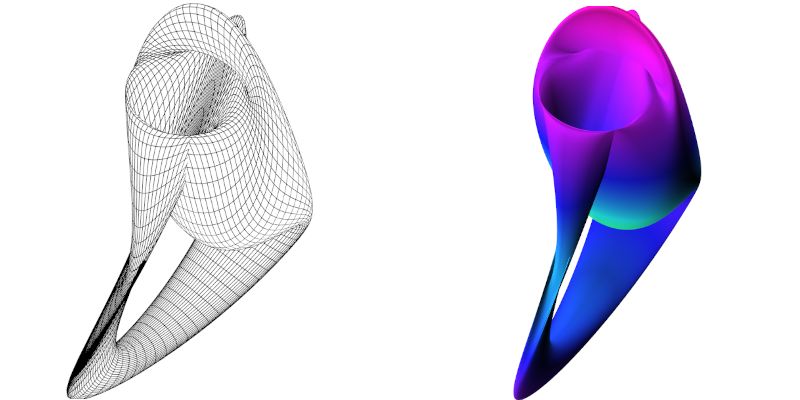
Funktion 6: Verdrehter Torus, Taste: '6'

Tx = 4*(1.5 * cos(x) * (1 + sin(y) * cos(x) - sin(2*y) * sin(x) / 2));
Ty = 4*(1.5 * sin(x) * (1 + sin(y) * cos(x) - sin(2*y) * sin(x) / 2));
Tz = 4*(1.5 * sin(x) * sin(y) +a*cos(x) * sin(2*y) / 2);


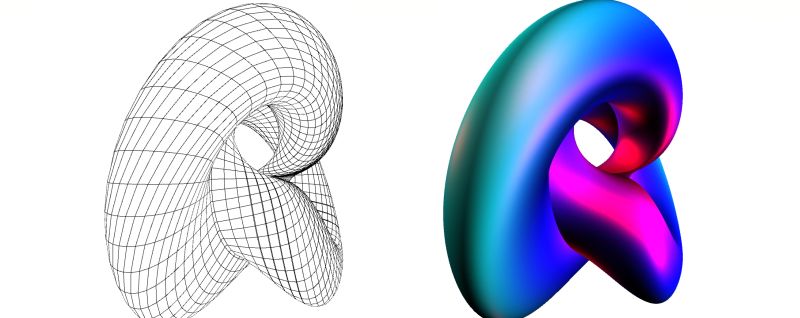
Funktion 7: Lemniscate, Taste: '7'

T1 = cos(y)/(1+sq(sin(y))); T2 = cos(y)/(1+sq(sin(y)))*sin(y);
Tx = 5*(1.5+T1*cos(5*x/2)-T2*sin(5*x/2))*cos(x);
Ty = 5*(1.5+T1*cos(5*x/2)-T2*sin(5*x/2))*sin(x);
Tz = 5*(T1*sin(5*x/2)+a*T2*cos(5*x/2));


Funktion 8: Torus, Taste: '8'

Tx = 1.5*(5+2*cos(x))*cos(y);
Ty = 1.5*(5+2*cos(x))*sin(y);
Tz = 1.5*a*2*sin(x);


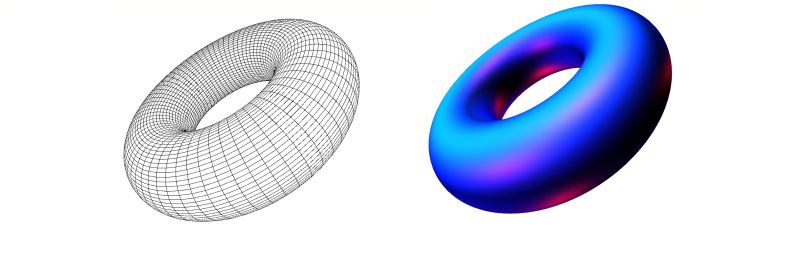
Funktion 9: Jeener-Klein entartet, Taste: '9'

T = 0.5*cos(2*x+PI/3)+3;
Tx = 3*a*(2*cos(x));
Ty = 3*T*sin(y);
Tz = -3*T*cos(y);


Funktion 10: Schnecke, Taste: 'ß'

T = exp(x/(6*PI));
Tx = 2.5*(2*(1-T)*cos(x)*cos(y/2)*cos(y/2));
Ty = 2.5*a*(1-exp(x/(3*PI))-sin(y)+T*sin(y))+10;
Tz = 2.5*(2*(-1+T)*sin(x)*cos(0.5*y)*cos(0.5*y));


Funktion 11: Neovius' Surface Variante, Taste: '?'

Tx = x*cos(x);
Ty = y*sin(x);
Tz = acos(-3*(cos(a*x)+cos(a*y))/(3+4*cos(a*x)*cos(a*y)));


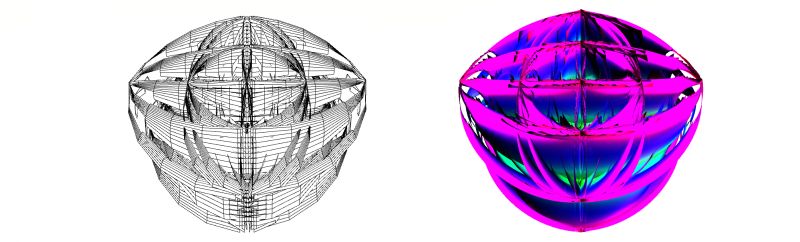
Funktion 12: Quadruple Point Cyclide, Taste: '§'

Tx = 30*cos(y)*sq(sin(y))*sin(y)*sin(2*a*x)*cos(a*x);
Ty = 30*cos(y)*sq(sin(y))*sin(y)*sin(2*a*x)*sin(a*x);
Tz = -30*cos(y)*sq(sin(y))*sin(2*x);


Funktion 13: Herz, Taste: '$'

Tx = 0.5*sin(y)*(15*sin(x)-4*sin(3*x));
Ty = 2*cos(y);
Tz = 0.5*sin(y)*(15*cos(x)-5*cos(2*x)-2*cos(3*x)-cos(2*x));

Narushin-Eier

Funktion 14: Egg Theory of Oomorphologie Valery Narushin, Taste '%'

T1 = B/2*sqrt((sq(L)-4*sq(x))/(sq(L)+8*W*x+4*sq(W)));
T2 = (sqrt(5.5*sq(L)+11*L*sq(W))*(1.732*B*L-2*D*sqrt(sq(L)+2*W*L+4*sq(W))));
T3 = 1.732*B*L*(sqrt(5.5*sq(L)+11*L*W+4*sq(W))-2*sqrt(sq(L)+2*W*L+4*sq(W)));
T4 = L*(sq(L)+8*W*x+4*sq(W));
T5 = (L-2*W)+sq(x)+(sq(L)+8*L*W-4*sq(W))*x+2*L*sq(W)+sq(L)*W+sq(L)*L;
Tx = 2*T1*(1-T2/T3*(1-sqrt(T4/T5)))*sin(2*y);
Ty = -2*x;
Tz = 2*T1*(1-T2/T3*(1-sqrt(T4/T5)))*cos(2*y);



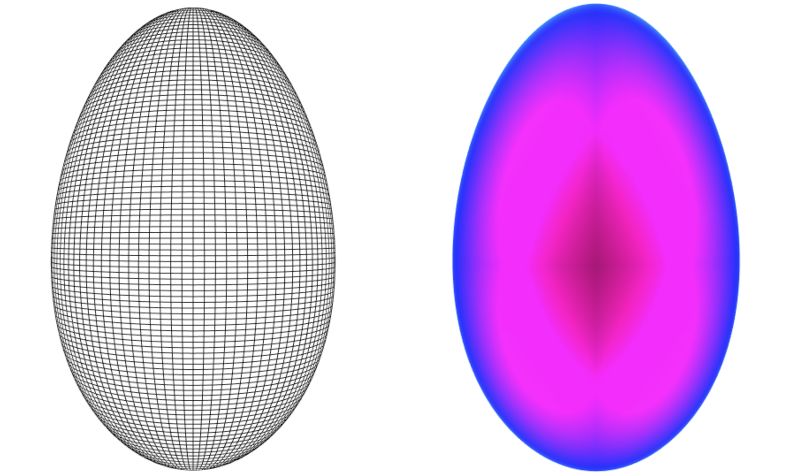
Diese "allgemeine Eierformel" hat Valeriy Narushin mit zwei britischen Kollegen in den Annals of the New York Academy of Science veröffentlicht. In zwei Dimensionen hat sie folgende Gestalt:


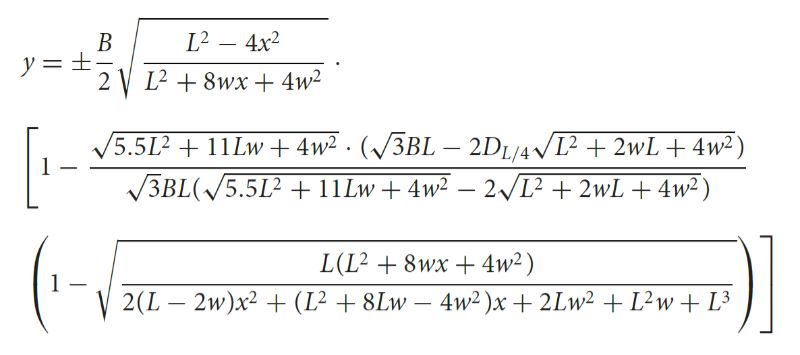
Diese Formel wurde hier auf drei Dimensionen erweitert. Vier Parameter bestimmen das Aussehen des Eis:

L: Höhe, B: maximale Breite, D: Breite bei L/4 und W: Abstand der Mitte von der breitesten Stelle. Mit Hilfe der Tasten b/B, d/D und w/W kann man die Parameter im interaktiven Sketch oben verkleinern bzw. vergrößern.

Sketch Parametrische Flächen

Menu