Fraktale: Julia versus Mandelbrot

Im Kapitel 10 des Lehrbuches wurden bereits einige Fraktale angesprochen. Die dort erwähnten klassischen Julia- und Mandelbaum-Fraktale werden mit einer einfachen Iteration erzeugt: 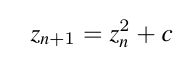Wenn jedem Pixel des Bildes einem c-Wert zugeordnet wird (Startwert ist z₀=0), berechnet man die Mandelbrot-Menge. Wird hingegen jedem Pixel ein Anfangswert z₀ zugeordnet, wird die (gefüllte) Julia-Menge erzeugt. Im einfachsten Fall wird das Pixel schwarz gefärbt, wenn nach n Iterationen der Abstand von z_n zum Ursprung kleiner oder gleich 2 ist. Andernfalls färbt man das Pixel weiß.
(Grund: Man kann zeigen, dass die Folge divergiert, wenn ein Element der Folge einen Abstand größer 2 vom Ursprung hat.)
Die Definitionsmenge und die Wertemenge der obigen Iteration ist die Menge der komplexen Zahlen mit Unendlich. Man kann sich diese Menge, die "Unendlich" enthält, durch die Oberfläche der Riemannschen Zahlenkugel veranschaulichen.



Erinnern Sie sich an das Feigenbaumdiagramm? Wenn man sich in der obigen Mandelbrot-Menge nur auf der gelben x-Achse bewegt, hat man es nur mit reellen Zahlen zu tun. Die beiden Iterationen (Feigenbaum/Mandelbrot) sind quadratisch. Man kann die Eine mittels linearer Transformation in die Andere überführen. Passt man die Koordinaten an, dann fällt auf, dass die Übergänge der kreisförmigen Elemente der Mandelbrotmenge mit den Verzweigungen des Feigenbaum-Diagramms übereinstimmen. (Rechts oben ist ein vergrößerter Abschnitt des blauen Bereichs links zu sehen.)
Hier können Sie den Sketch LogMandelbrotFeigenbaum für eigene Experimente runterladen.

Was bedeuten die Verzweigungen im Feigenbaum-Diagramm in der Mandelbrot-Menge? Das können Sie im folgenden Sketch selbst ausprobieren:

Schauen wir uns die Sache etwas genauer an: Im Bild ganz oben ist ein Punkt D markiert. Es gilt hier: c = -1,3 + 0*i. Im Feigenbaumdiagramm darüber sind vier Punkte (schwarz) markiert. Wir erinnern uns, dass die Werte der Iteration erst dann eingetragen werden, wenn eine vorher festgelegte Zahl m erreicht wurde. Auf diese Weise kann man den "Einschwing-Vorgang" unterdrücken.

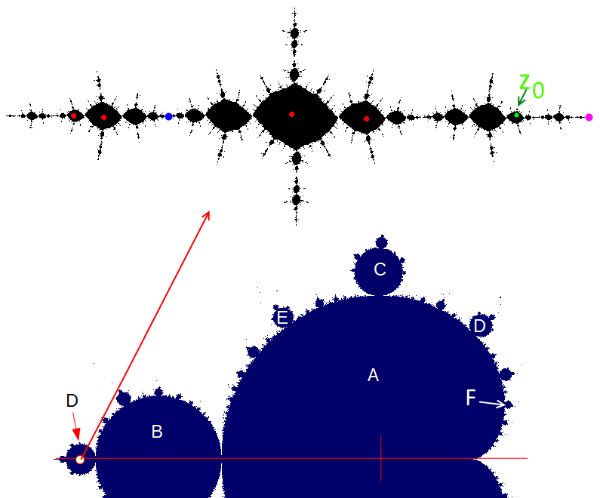
Wenn man im obigen interaktiven Sketch im Kreis-ähnlichen Abschnitt D auf der reelen Achse einen Linksklick ausführt, bekommt man in etwa die gefüllte Juli-Menge im Bild darüber. (Achtung! Es gibt zwei Abschnitte mit dem Buchstaben D. Finden Sie heraus, warum beide den gleichen Buchstaben bekommen haben!)
Als Startpunkt wurde per Rechtsklich der grün eingetragen Punkt z₀ gewählt. Die Punkte des Orbits (rot) werden erst ab Folgenglied m = 500 eingetragen. Solange sich der Startpunkt im Innern befindet, werden immer diese vier Punkte angenähert. Mit Taste 'f' schließlich kann man sich die beiden Fixpunkte eintragen lassen. Magentafarben ist der instabile-, blaue der stabile Fixpunkt. Wir kommen weiter unten darauf zurück.

Lässt man sich (mit Shift + Rechtsklick) auch die Orbit-Punkte ab dem ersten Element zeigen, so erkennt man, dass die Folge sehr schnell zu dem rot markierten Vierer-Zyklus konvergiert.
Um den Überblick nicht zu verlieren, machen Sie sich bitte klar, dass ein Startpunkt z₀ in der gefüllten Julia-Menge den tatsächlichen Startpunkt der Folge darstellt, während in der Julia-Menge ein mit Linksklick ausgewählter Punkt die Konstante c bestimmt.
Sie könnten nun die reelle Achse verlassen und einen beliebigen c-Wert aus den Gebieten A,B,C,D oder E für die gefüllte Julia-Menge wählen:

Die obige Auswahl an gefüllten Julia-Mengen legt eine sehr einfach durchschaubare Systematik von zyklischen Attraktoren nahe. Allerdings wurden die verschiedenen c-Werte immer nahe des Zentrums einer (nahezu) kreisförmigen Teilmenge gewählt. So vermutet man, dass im Gebiet F möglicherweise ein 6-er Zyklus zu finden sein wird. Und tatsächlich wird diese Vermutung mit Hilfe des Sketches auf dieser Seite sehr schnell bestätigt. Was passieren kann, wenn man andere c-Werte wählt, schauen wir uns nun im folgenden an:



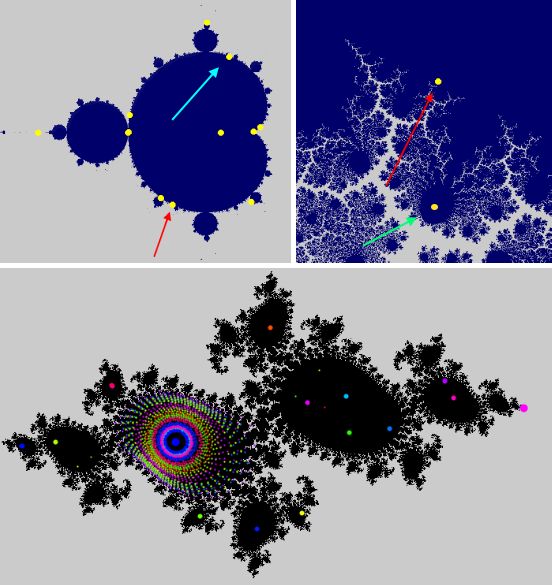
Gehen Sie zurück zum obigen Sketch, aktivieren den Sketch mit einem Rechtsklick und drücken danach Taste c (Bild links oben). Suchen Sie sich einen der gelben Punkte aus, vergrößern mit Shift+Linksklick vier bis fünf mal (Bild rechts daneben) und lassen sich mit Shift+Rechtsklick die Folgenglieder von Beginn an zeigen. Bei jedem neuen Startpunkt wird eine neue Farbe verwendet.
Wie Sie sehen können, gibt es zwar noch die beiden Fixpunkte (Taste f), aber von einem zyklischen Attraktor kann man hier offensichtlich nicht mehr sprechen.
Und noch etwas fällt auf: Der c-Wert, auf den der rote Pfeil zeigt, scheint in der Mandelbrotmenge zu liegen. Und wie sieht es mit dem c-Wert, auf den der grüne Pfeil zeigt aus? Lassen wir uns dort die zugehörige gefüllte Juliamenge zeigen (Bild unten), dann erkennt man deutlich, dass diese Menge, im Gegensatz zu oben, nicht mehr zusammenzuhängen scheint.

Dieser Sachverhalt wird noch deutlicher, wenn man die Iterationsgrenze erhöht. Das allerdings lässt sich nur recht mühsam mit obigem Sketch zeigen. Die Rechnung dauert schlicht zu lang. Für diese Untersuchungen verwendet man besser unseren Multithread-Julia Sketch. Dort kommt dann auch eine Klasse Complex zum Einsatz.

Weiter oben können Sie einen türkisfarbenen Pfeil erkennen, der auf einen der besonderen c-Werte zeigt (gelb). Genau dort zoomen wir mehrere Male ins Bild und stellen fest, dass wir dort offensichtlich zwei verschiedene Punkte festgelegt haben. "Lesen" Sie die Bilder von links nach rechts und von oben nach unten.


Die weißen Zahlen geben die Anzahl der Iterationen wieder. Zu Beginn scheinen beide c-Werte innerhalb der Mandelbrot-Menge zu liegen. Iteriert man aber über 40000 mal, dann wird offensichtlich, dass lediglich der untere Wert noch in besagter Menge liegt.
Die darunter dargestellten zugehörigen gefüllten Julia-Mengen unterscheiden sich erheblich. Beide Bilder entstanden durch 43000-fache Iteration. Die links dargestellte Menge zum außerhalb liegenden c-Wert besteht nur noch aus einzelnen Punkten, die nicht zusammenzuhängen scheinen. Nur die Orbits sehen noch ähnlich aus. Wenn Sie nun in beiden Fällen die Iterationsgrenze zum Beispiel verdoppeln, verschwindet das Bild links vollständig, während auf der rechten Seite eine zusammenhängende Punktemenge erhalten bleibt.
Diese Besonderheit werden wir im folgenden Kapitel genauer untersuchen.

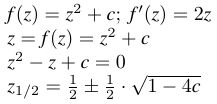
Was hat es mit den oben erwähnten Fixpunkten auf sich? Wir wissen aus dem Kapitel Standard Map, dass bei der Untersuchung der Struktur einer Abbildung, den Fixpunkten eine besondere Bedeutung zukommmt. Das ist hier nicht anders.
Links sind alle benötigten Rechnungen dargestellt. Sobald ein Wert für c festgelegt ist, erhält man die zwei Fixpunkte. (Im Fall von c = 0.25 gibt es nur einen Fixpunkt: 0.5)
Der Betrag der Ableitung lässt auf die Art des Fixpunktes schließen: Ist der Betrag 0, dann handelt es sich um einen "stark anziehenden" Fixpunkt. Liegt der Betrag der Abbleitung zwischen 0 und 1, dann ist der Fixpunkt nur noch "anziehend". In beiden Fällen ist ein solcher Fixpunkt ein Attraktor . Ist der Betrag der Abbleitung 1, dann verhält sich der Fixpunkt "indifferent". Für Beträge größer 1 schließlich ist der Fixpunkt "abstoßend".

Mit diesem Hintergrundwissen wollen wir nun die Menge aller Punkte (c-Werte) in der Mandelbrot-Menge finden, für die die Julia-Menge einen indifferenten Fixpunkt besitzt. Hier sind die Rechnungen und das Ergebnis (rot):

Die Punkte auf der Mandelbrotmenge, die zu einem indifferenten Fixpunkt führen, wurde mit dem Sketch Julia-Parameter durchgeführt. Wie man sofort erkennnt, ist das Ergebnis genau der Rand der großen herzförmigen Fläche.
Wenn man für α = 2π/k , mit k = 2,3,4,5...wählt, bekommt man genau den Ansatzpunkt der "Knospen", die an der Hauptfläche sitzen. Mit k bekommt man dann auch gleichzeitig die Periode des zugehörigen Attraktors der gefüllten Julia-Menge geliefert: Mit dem schon erwähnten Sketch Julia-Parameter können Sie das selbst überprüfen. Sehr praktisch: Wenn Sie für k eine beliebige Zahl wählen und sich alle zugehörigen c-Werte berechnen lassen, für die die zugehörigen gefüllten Julia-Mengen einen indifferenten Fixpunkt besitzen, dann führen alle unmittelbar angrenzenden "Knospen" zu c-Werten, für die die gefüllten Julia-Mengen einen Attraktor der Periode k besitzen. Klingt komplizierter, als es ist. Ein Bild und ein eigenes Experiment verschafft Klarheit:
Im obigen interaktiven Sketch ist schon alles für die Periode 37 vorbereitet. Mit der Taste p kann man sich, sofern die Mandelbrot-Menge angezeigt wird, alle c-Werte mit den beschriebenen Eigenschaften anzeigen.
Für die Winkel gilt dann: α = i⋅2π/37 ; i = 1,2,3,...,36


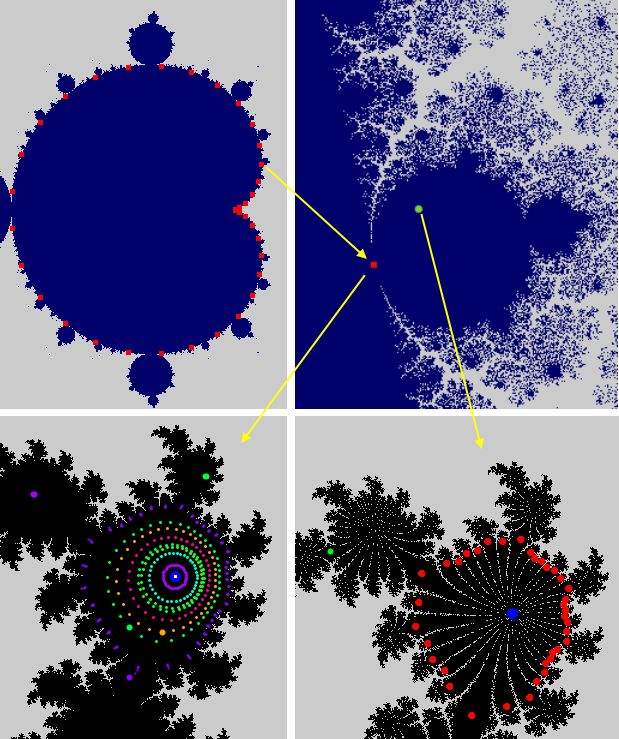
Oben links sind die beschriebenen 36 c-Werte rot eingetragen. Links daneben nach mehreren Vergrößerungen (Shift + linke Maustaste) sieht man noch einen davon und in grün einen in der anliegenden "Knospe" liegenden c-Wert. Links unten das Ergebnis der gefüllten Julia-Menge, die, wie man sehr gut erkennen kann, einen indifferenten Fixpunkt besitzt. Rechts daneben, zum grünen Punkt gehörend, die gefüllte Julia-Menge mit einem Attraktor der Perionde 37.