Lyapunov 1
Lyapunov Exponent
Im Kapitel "Dynamische Systeme" gibt es einen Abschnitt Lyapunov-Exponent. Wenn Sie noch nicht wissen sollten, was ein Lyapunov-Exponent ist, dann sollten Sie diesen Abschnitt zuerst lesen.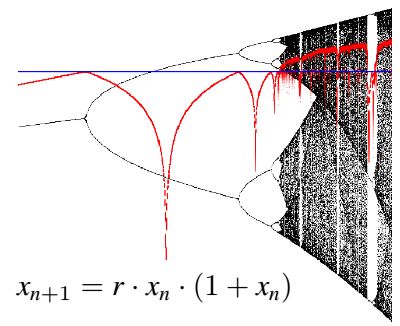
Zu dieser Iteration, die zum sogenannten Feigenbaum-Diagramm
führt (siehe Bild links), haben wir dort den Lypapunov-Exponenten λ errechnet.
Für jeden Parameter r zwischen 1,1 und 3,9 erhält
man eine andere Folge und damit ein anderes λ. Die blaue Linie ist die Null-Linie
für λ , die schwarzen Punkte zeigen den Verlauf der Iteration für einen bestimmten Parameter r
an (r wird nach rechts abgetragen) und die roten Punkte schließlich zeigen den dort gültigen Wert für λ.Wichtig ist auch, dass die Werte der Iteration erst ab einem bestimmten Folgeglied eingetragen werden. Denn so kann man auf einen Blick erkennen, ob die Folge gegen einen, zwei oder mehrere Grenzwerte konvergiert. Für kleine Werte von r gibt es nur einen, ab einer bestimmten Größe von r dann zwei alternierend angenommene Grenzwerte. Wird r noch größer, kommt es zu chaotischen Folgen ohne Grenzwerte. Das Schaubild von λ zeigt das durch das Vorzeichen an. Bei positivem λ ist die Folge chaotisch. Ist λ Null, gibt es dort eine Veränderung des Verhaltens der Folge. Ganz links wäre das der Übergang von einem zu zwei Grenzwerten. Negative Werte von λ garantieren eine zu einem oder mehreren Grenzwerten konvergente Folge.
Lyapunov "Fraktale"
Weshalb ist das Wort Fraktale in der Überschrift in Anführungszeichen? Die Antwort ist einfach: Weil die meisten Bilder, die mit den im Folgenden dargestellten Alogrithmen erstellt werden, keine Fraktale sind, aber dennoch recht häufig so genannt werden. Sie werden feststellen, dass "Selbstähnlichkeit", ein bei echten Fraktalen vorkommende Eigenschaft, hier fehlt. Auch hier werden die mit dem "Lyapunov-Algorithmus" erstellten Bilder als "Fraktale" bezeichnet. Einfach deswegen, weil die Mehrheit derjenigen, die echte oder unechte Fraktale erzeugen, in keinster Weise an der gebrochenen Dimension, die zwischen echt und unecht unterscheidet, interessiert sind. Sie wollen eindrucksvolle Bilder kreieren und pfeifen auf Selbstähnlichkeit und gebrochene Dimension.Damit man ein Bild wie zu Beginn des Kapitels erzeugen kann, muss man aus dem eindimensionalen Lyapunov Exponent (Variable ist r) eine zweidimensionale Vorschrift erzeugen. Dazu wählt man einfach einen zusätzlichen Parameter r2. Der ursprüngliche Wert r wird nun r1 genannt. Jeder Punkt der Ebene, für den man den erweiterten Lyapunov Exponent berechnen will, liefert mit seinen Koordinaten r1 und r2.
Worin besteht nun die "Erweiterung"? Man definiere eine endliche Folge aus den Elementen A und B, wie beispielsweise AABABB, die dann dadurch eine unendliche Folge wird, dass man die endliche Folge immer wieder hinten anhängt:AABABB AABABB AABABB....
Bei jeder neuen Iteration geht man einen Schritt in dieser Folge weiter. Kommt man auf ein A, so wählt man r1 als Parameter, im anderen Fall r2.
Wählen wir als Definitionsbereich für die Parameter ri 2 <= r1 , r2 <= 4 und führen dann den oben beschriebenen Algorithmus mit der Folge AB der "Feigenbaum-Iteration" aus, dann erhält man bei geeigneter farblicher Zuordnung der Funktionswerte von λ das folgende Bild:
Die farbliche Zuordnung wird mit den verschiedenen Farb-Tafel-Klassen erledigt: Im Fall von positivem
λ (und λ = 0), also bei Chaos, geht die Zuordnung von schwarz nach blau,
das heißt, je größer λ, desto heller die Farbe.
Bei negativem λ wurde hier der Farbverlauf schwarz - rot - gelb gewählt.
Bleibt man bei einer bestimmten Folge, dann gibt es zwei verschiedene Möglichkeiten, das Bild
zu verändern: Entweder wählt man eine andere Folge aus A und B (in den Sketchen durch die Taste 'a')
oder man ordnet die Werte von λ auf eine andere Art den Farben zu (durch die Tasten '1' bis
'7').
Bei dieser Zuordnung gibt es ein prinzipielles Problem: Die Werte von λ müssen mit einem
geeigneten Faktor multipliziert werden, damit man für eine Farbtafel, bestehend zum Beispiel aus 1024
Farben, sinnvoll zuordnen kann. Für ein 400x400 Pixel großes Bild liefert die hier verwendete Folge eine
Verteilung der Werte -Faktor*λ im Fall von negativem λ:
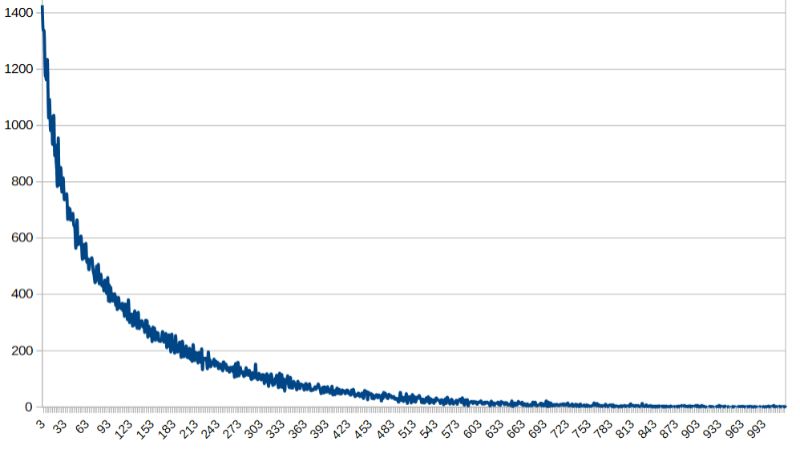
Aus dem Schaubild kann man entnehmen, dass -Faktor*λ= 33 ca.1000 mal vorkommt. Um dennoch
plastische wirkende Bilder zu erhalten, wurde bei der linearen Farbzuordnung nur (-Faktor*λ)-Werte
bis 512 verwendet. Die anderen Ergebnisse fielen unter den Tisch. In diesem Fall sind die Ergebnisse dennoch
ganz ordentlich, bei anderen Folgen wird man aber nur unzureichende Ergebnisse bekommen, wenn man einfach
die größten Werte von -λ einfach abschneidet.
Aus diesem Grund verwenden wir, neben der linearen Zuordnung, eine "gerechte" Zuordnung. Aufgrund des
Logarithmus sind die λ-Werte in aller Regel irrational, d.h. solange man nur einen groß genugen Faktor
wählt, sind die (-Faktor*λ)-Werte fast alle verschieden. In den Sketchen wählen wir den Faktor so groß,
dass der maximale (-Faktor*λ)-Wert 100 000 ist. Nun muss man nur noch wissen, wie viele Pixel ein
negatives Lambda bekommen (jeder Thread zählt für sich - und am Ende werden die einzelnen Werte addiert),
Nehmen wir an, es soll ein 1200*1200 Pixel großes Bild erzeugt werden und bei 10 Millionen Pixeln wäre der Wert
von Lambda negativ. Dann stehen jedem negativen Lamda 10 000 000 : 100 000 = 100 Werte zu.
Nun muss man einfach nur zählen, bis die hundert erreicht sind. Beipiel:
1: 12, 2: 13, 3: 15, 4: 28, 5: 30 (bis hier 98 Werte), 6: 44. Das heißt nun, dass alle (-Faktor*λ)-Werte
zwischen 1 und 5 dem Farbwert 0 zugeordnet werden.
(Die dazu notwendigen Schritte werden nach jedem Programmstart durchgeführt. Allerdings muss zunächst mindestens
einmal eine lineare Farbzuordnung - Tasten '1' bis '5' - durchgelaufen sein, damit die notwendigen Tabellen
erstellt werden können. Danach kann man mit den Taste '6' und '7' die "gerechte" Zuordnung verwenden.)
Die Wirkung dieser Methode kann man im folgenden Bild sehr gut beobachten: Der graue Bereich (Lambda negativ)
hat nun feine Übergänge. Das Bild wirkt plastischer. Die Zuordung im Chaos-Bereich ist hier, im Gegensatz
zu den beiden Bildern oben, linear mit einem Farbverlauf kodiert - also nicht mit hell/dunkel einer Farbe. Einen
direkten Vergleich zwischen "gerechter" und linearer Farbkodierung kann man gekommen, wenn man für den ersten
Fall Taste '6' und für den zweiten Fall Taste '5' drückt.
Im Bild oben wurde gezoomt, die Reihenfolge von A und B durch Taste 'a' verändert und "gerechte"
Farbzuordnung gewählt. Solange man die zugrundliegende Folge nicht verändert, könnte man zusätzlich den ersten Wert
x0, die Anzahl der Iterationen, die man nicht beachtet, und schließlich auch die Grenze der Iteration
verändern. Große Änderungen des Bildes darf man bei den drei letztgenannten Möglichkeiten aber nicht erwarten.
Viel interessanter ist das Verändern der Folge. Und genau das wird im
nächsten Abschnitt gezeigt.
Menu