Doppelpendel Map

Maps

Doppelpendel-Map

Das Doppelpendel hat uns in den Kapitel Simulationen und Dynamische Systeme bereits ausführlich beschäftigt. Es gelang uns recht mühsam, ein Phasendiagramm zu erstellen. Dabei wurde in der Simulation immer dann ein Punkt ins Phasendiagramm eingetragen, wenn das untere Pendel von rechts kommend durch die Ruhelage schwang. Man braucht wirklich Geduld, um bis eine Trajektorie, die aus mindestens 100 Punkten (besser 500) bestehen sollte, gezeichnet wird. Das soll hier nun wesentlich schnell gehen. Wir hätten gerne ein Bild wie links, auf dem etwa 500 Startpunkte und je Startpunkt 5000 Folgepunkte eingetragen sind. (Das Bild hat im Original 1500 x 1500 Pixel.)

Umgangssprachlich bezeichnet man häufig auch das Phasendiagramm mit all seinen Trajektorien, wie im Bild links, als Map. Man sollte dennoch wissen, dass für Mathematiker eine Map eine Abbildung ist (bijektive und stetige Abbildung eines euklischen Raumes auf sich selbst). Vereinfachen wir: Eine Map ist eine Abbildung, bei der nur ein Aspekt wichtig ist: Wo landet der Punkt P unter eben dieser Abbildung? Sagen wir, er landet bei P'. Nächste Frage: Wo landet P' unter der gleichen Abbildung? Zum Schluss muss man noch verstehen, dass man nun nur noch den besagten Punkt P mit einem beliebigen Punkt des Phasendiagramms identifizieren muss. P kann also ein Startpunkt eines Phasendiagramms sein. P' ist dann ebenfalls ein Punkt im Phasendiagramm. Und zwar derjenige, der nach einer festgelegten Zeit t erreicht wird.
Sie können das im folgenden Sketch selbst ausprobieren. (Die Animation des Pendels wurde weggelassen, damit die Zeichnung der Trajektorien etwas schneller geht.) Es werden fünf Startpunkte gewählt und mit diesen jeweils die 500 nächsten Folge-Punkte errechnet und im Phasendiagramm eingetragen. Dies geschieht, was die beiden Winkel und die Winkelgeschwindigkeit des unteren Pendels angeht, zufällig. Über den Energieerhaltunssatz bekommt man eine quadratische Gleichung für die fehlende Winkelgeschwindigkeit, so dass alle Trajektorien zur gleichen Energie E gehören.
Sobald man auf das Diagramm klickt, werden zu den nächsten fünf zufälligen Startpunkten die Folge-Punkte errechnet und eingetragen. Es gibt hier bei E = 1000 fast nur kreisähnliche Trajektorien. Es lassen sich auch mehrere "Inseln" ausmachen. Dies sind allesamt quasiperiodische Bereiche. Die Zentren der Inseln liefern sogar eine periodische Bewegung des Doppelpendels. Die Trajektorien sind hier ziemlich breit und ungenau. Das liegt daran, dass für die Simulation relativ große Zeitschritte gewählt wurden, damit Sie nicht zu lange auf das Ergebnis warten müssen.
Vergessen Sie nicht, dass nur dann ein Phasenpunkt eingetragen wird, wenn das untere Pendel von rechts durch die Ruhelage schwingt. Wir können als keine explizite Map-Funktion angeben.

Wenn die Rechnung noch schneller gehen soll, dann sollte man die Aufgabe auf möglichst viele Thread verteilen. Weiter unten können Sie auch eine Threaded-Version für die Doppelpendel Poincaré-Schnitte runterladen. Hat der Prozessor z. B. 16 Core , dann braucht die Erzeugung des Bildes nur etwa 1/12 der Zeit wie bei einem einzigen Thread. Mehr dazu im Kapitel Threads.

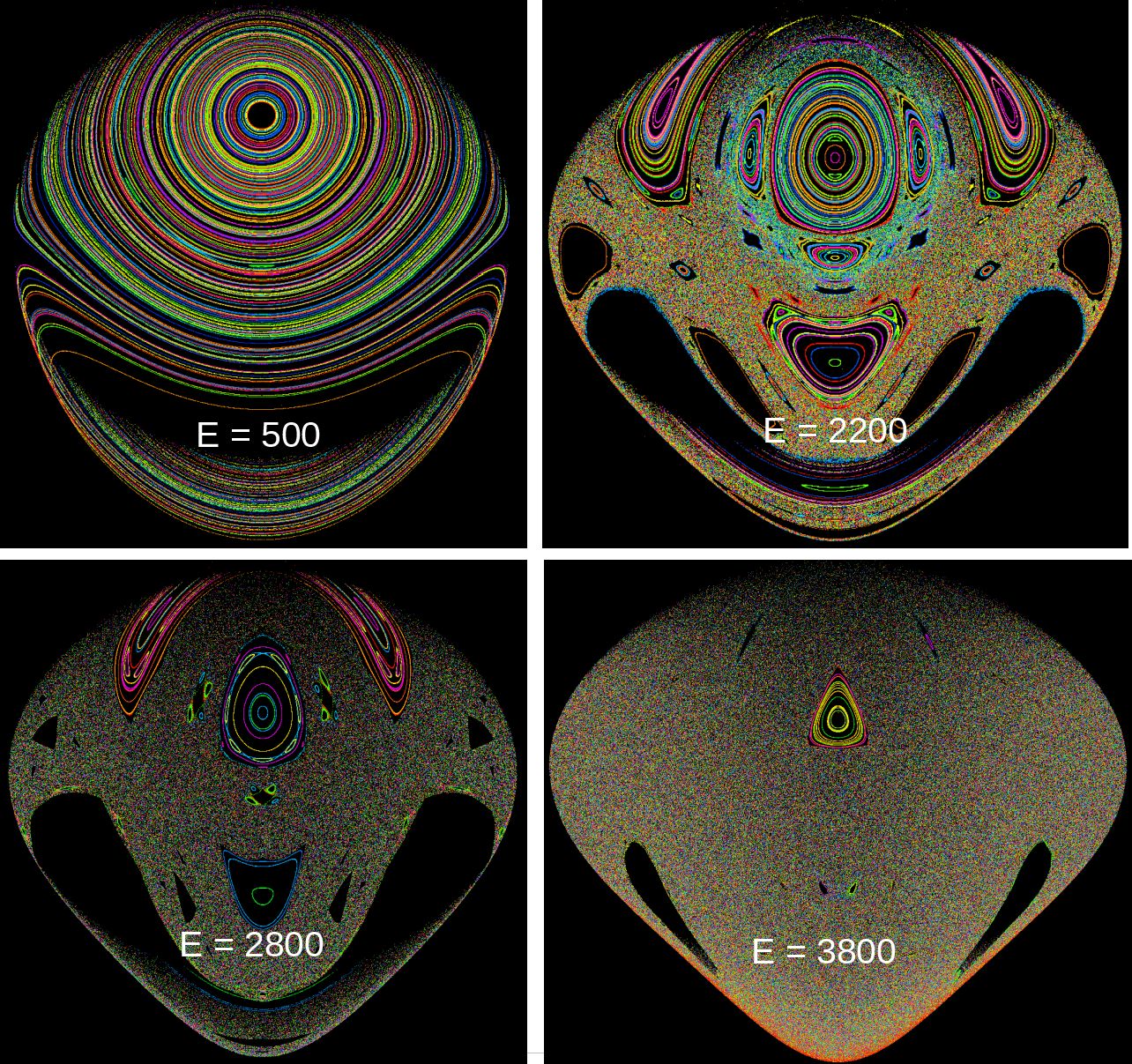
Die obigen Bilder wurden mit dem Sketch DoppelPendelPoincareThreadedFastZoom erzeugt. Man erkennt, dass je größer die Gesamtenergie ist, desto größer ist das "chaotische Meer".
Können Sie im Bild ganz oben für E = 1700 in etwa die "Seperatix" erkennen?

Im Kapitel Dynamische Systeme wurde erwähnt, dass der sogenannte Cantorus fraktal ist. Das können Sie ebenfalls mit dem Sketch DoppelPendelPoincareThreadedFastZoom ausprobieren. Obwohl das Programm (z. B. bei üblichen Quadcor-Prozessoren) wegen der Thread-Technik und der Verwendung zweier verschiedener Zeitabschnitte, etwa 70 mal schneller ist, als das Standardprogramm, kann das Errechnen eines Bildes, je nach Anzahl der gewünschten Trajektorienpunkte, gut und gerne eine Stunde und mehr benötigen, wenn man die Voreinstellungen für die beiden Zeitabschnitte übernimmt. Diese sind mit 0.001 und 0.0001 sehr klein. Dadurch werden, zumindest bis zum 2. Mal zoomen, die Trajektorien sehr exakt gezeichnet. Theoretisch könnte man auch noch ein 3. Mal zoomen, nur werden dann bei dieser 125-fachen Vergrößerung die Linien bei diesen Zeitwerten etwas breiter.

Sketch mapDoppelPendelPoincare .

Sketch DoppelPendelPoincareThreadedFastZoom .

Menu