Simulation
Kicked Rotator
Stellen Sie sich ein mathematisches Pendel vor, das reibungsfrei und schwerelos seine Bahnen zieht. Die Winkelgeschwindigkeit wäre konstant. Und damit trifft die Bezeichnung "Pendel" nicht mehr zu. Solche Apparate nennt man "Rotator". Das Adjektiv "kicked" soll andeuten, dass der Rotator periodisch für jeweils sehr kurze Zeit eine Kraft erfährt, die immer gleich groß und auch immer gleich gerichtet ist. Man kann sich also vorstellen, dass das Schwerefeld in immer gleichen Zeitabschnitten kurz wirksam ist. (Wem diese Vorstellung verständlicherweise Schwierigkeiten macht, denkt sich stattdessen eine eisernen Kugel am Ende des schwerelos gedachten Stabes. Der Stab rotiert horizontal und das Magnetfeld wird in immer gleichen Zeitabschnitten ganz kurz eingestellt.) Hier finden Sie weitergehende Erklärungen zum periodisch angestoßenen Rotator, wie der Kicked Rotator auch genannt wird.
Weshalb behandeln wir ein solch seltsames Modell. Hat es denn überhaupt eine, über das konkrete Experiment hinausgehende, Bedeutung? Und ob! Wenn Sie sich im Abschnitt Maps die "Standard-Map" ansehen, werden Sie erfahren, dass Probleme aus Medizin, Astrophysik, Chemie und Quantenmechanik immer wieder bei diesem Modell des "periodisch angestoßenen Rotator" landen.
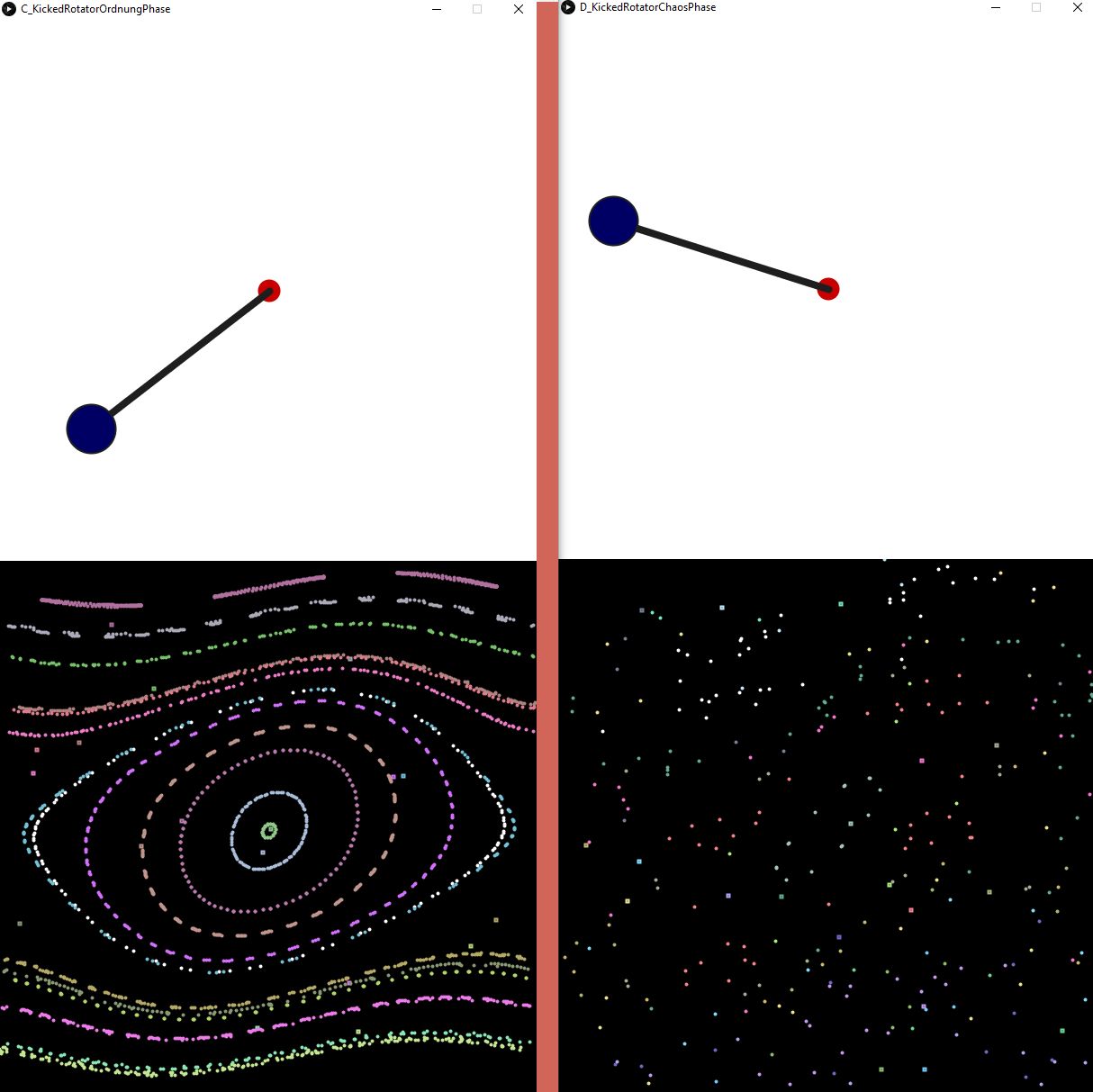
Wenn man das Phasendiagramm auf der linken Seite mit dem auf der rechten Seite vergleicht und wenn man sich weiterhin vergegenwärtigt, dass ein Punkt an einer bestimmten Stelle einen konkreten Winkel und eine bestimmte Winkelgeschwindigkeit zu einem bestimmten Zeitpunkt repräsentiert, dann vermutet man, dass die Situation rechts Chaos anzeigt. Die ellipsen-ähnlichen Gebilde links deuten darauf hin, dass der Rotator, ohne sich zu überschlagen, von einer Seite auf die andere Seite pendelt. Die "verbogenen" Strecken hingegen stehen für sich permanent überschlagende Rotoren. Beim Kicked Rotator hat man drei Freiheitsgrade: Winkel w, Winkelgeschwindigkeit g und Frequenz des Kraftstoßes. Man kann daher eigentlich kein zweidimensionales Phasendiagramm zeichnen, - es sei denn, wir legen fest, dass immer dann, wenn der Kraftstoß erfolgt, g und w gemessen und im Phasendiagramm eingetragen werden. Woran liegt es nun, dass sich der Rotator einmal chaotisch und ein andermal recht regelmäßig verhält? Um ein derartiges Experiment durchzuführen, benötigt man die Startwerte von Winkel und Winkelgeschwindigkeit und die Größe der periodisch wirksamen Kraft. Im einen Fall sind sie so gewählt, dass Choas wahrscheinlicher und im anderen, dass Ordnung wahrscheinlicher ist. Die Anfangbedingungen können Sie selbst wählen. Wenn Sie es ausprobieren wollen, hier die Links:
Kicked Rotator OrdnungKicked Rotator Chaos
Den theoretischen Hintergrund dieses und weiterer Geräte, die recht schnell im Chaos landen, können Sie im Kapitel Dynamische Systeme den Abschnitt Wege ins Chaos studieren. Dort selbst werden Sie dann recht schnell in den Kapitel Maps bzw. Fraktale landen. Denn es gibt viele Seiten, sich dem Chaos zu nähern...
Sketch KickedRotatorOrdnung .
Sketch KickedRotatorChaos.
Menu