Kryptologie
One-Time-Pad mit Clifford Attraktor
Es geht in diesem Kapitel um zwei Dinge: Wie kann man in Processing auf Bit-Ebene die XOR Verknüpfung darstellen
und wie erzeugt man mit Hilfe des
Clifford Attraktore ein
One-Time-Pad ?
Ein One-Time-Pad ist ein "Einmalschlüsselung-Verfahren", das eine Schlüssel verwendet, der mindestens so lange ist,
wie die Nachricht. Mit einem Schlüssel, der echt zufällig ist und auch nur ein einziges Mal verwendet wurde,
kann die Nachricht nicht entschlüsselt werden. Das ist keine Vermutung: Es ist mathematisch beweisbar!
Wer es genauer wissen will, schaut
hier nach.
Der Haken an der Sache: Es ist nicht einfach, einen wirklich zufälligen Schlüssel zu erzeugen! Eine Methode wäre,
radioaktiven Zerfall zu verwenden. Hat man bei einer radioaktiven Probe festgestellt, dass mit 50%-iger Wahrscheinlichkeit
zehn Teilchen innerhalb einer Sekunde zerfallen, dann wählt man 1, falls dies zutrifft und 0 in gegenteiligen Fall.
Mühsam! Man sucht daher Funktionen, die dem Zufall nahe kommen. Die einfachste ist random() in Java und Processing.
Leider ist sie in keinster Weise sicher. Deutlich besser ist die Methode SecureRandom(), die aktuelle Daten des Betriebssystems
mit verwendet.
Wir benutzen eine Variante des chaotischen Clifford Attraktors.
Man erzeugt damit eine komplizierte Menge fraktalen Charakters. Das chaotische System erzeugt man durch
genügend lange Iterationen der dynamischen Clifford Iteration.
Wie die Abbildung genau aussieht, lesen Sie dort im Abschnitt Clifford Gleichungen als partielle Ableitungen interpretiert .
Eine wesentliche Eigenschaft, die die Abbildung haben sollte, ist eine hohe Empfindlichkeit (sensitivity) von den Parametern,
die als Schlüssel dienen. Genau das aber ist bei chaotischen Abbildungen der Fall. In unserem Fall wird es fünf achtstellige
Parameter geben. Falls nur eine der 40 Ziffern verändert wird, ist keine (auch teilweise) Entschlüsselung mehr möglich.
Zudem sollten die, durch die Clifford Abbildung erzeugten möglichen Ergebnisse, gleichverteilt sein. Dies ist, wie
wir sehen werden, ebenfalls erfüllt. Es ist bei chaotischen Abbildungen gänzlich unmöglich, einen Folgewert aus
den vorhergehenden zu bestimmen, ohne den Algorithmus und die Paramter genau zu kennen .
Zur XOR Verknüpfung auf Bit-Ebene:
Zunächst bestimmen wir auf übliche Weise zwei Zufallsfarben (farbe1,farbe2) und bringen sie in ihre Einzel-Bit Darstellung.
int r = int(red(farbe1)) << 16;
int g = int(green(farbe1)) <<8;
int b = int(blue(farbe1));
int A = int(alpha(farbe2)) << 24;
int R = int(red(farbe2)) << 16;
int G = int(green(farbe2)) << 8;
int B = int(blue(farbe2));
farbeBin1 = a | r | g | b;
farbeBin2 = A | R | G | B;
11111111 00000000 00000000 00000000
00000000 00100001 00000000 00000000
11111111 00100001 00000000 00000000
Nach der Zeile farbeBin1 = a | r | g | b haben alle Bits ihren der Farbe entsprechenden Wert. Mit fill(farbeBin1) kann man das obere Quadrat einfärben. Entsprechend verfährt man beim 2. Quadart.Die XOR-Verknüpfung (ausschließendes oder) ist definiert durch: 0 | 0 = 0 und 1 | 1 = 0. Bei verschiedenen Bit-Werten erhält man 1. So funktioniert die XOR-Verknüpfung in Java:
int rr = r ^ R;
int gg = g ^ G;
int bb = b ^ B;
farbeBin3 = aa | rr | gg | bb;
01100100 10001100 00110101 farbeBin1
00100001 01011100 11110000 farbeBin2
01000101 11010000 11000001 farbeBin1 XOR farbeBin2
00100001 01011100 11110000 farbeBin2
01100100 10001100 00110101 (farbeBin1 XOR farbeBin2) XOR farbeBin2
Wie Sie sehen, erhält man nach der wiederholten XOR-Verknüpfung mit farbeBin2 wieder den ursprünglichen Farbwert farbeBin1. Die zweite Farbe kann man zur Verschlüsselung der ersten Farbe verwenden. Sie ist offensichtlich der Schlüssel für beide Vorgänge: Zum Ver- und Entschlüsseln der Ursprungsfarbe.Damit bekommt man ein Verfahren zur Ver- und Entschlüsselung eines Farbbildes, in dem man das beschriebene Verfahren auf jedes Pixel anwendet. Die Bilddimensionen müssen dabei mit den Schlüsseldimensionen übereinstimmen. Im Folgenden versuchen wir (der Einfachheit halber für ein Graustufenbild) einen Schlüssel zu erzeugen, der hinreichend "zufällig" ist.
Den Sketch zur Erzeugung des Schlüssels können Sie sich hier runterladen. Alle notwendigen Erläuterungen findet man im Kapitel Clifford Attraktors . Die fünf zu wählenden Parameter können zum Beispiel so aussehen:
Wir gehen davon aus, dass ein Graustufenbild der Dimension 1000x1000 verschlüsselt werden soll. Ändern Sie
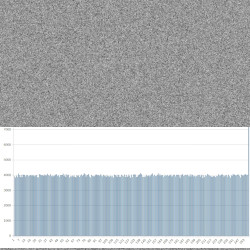
gegebenenfalls size() zum Bild passend. Nachdem der Sketch gestartet wurde, findet man bild2.bmp wie links (ohne Diagramm) im Programmordner. Jedes Pixel hat einen Grauwert zwischen 0 und 255. Diese Werte sollten unbedingt gleichverteilt sein. Das Programm ist bereits auf die Kontrolle vorbereitet. In der Console wird die Anzahl der Pixel mit Wert n ausgegeben. Wir kopieren diese Daten in Exel oder in Libre Office Calc und lassen uns das zugehörige Balkendiagramm anzeigen. Wie man links erkennen kann, ist die Gleichverteilung perfekt.
Kommen wir nun zum eigentlichen XOR-Verschlüsselungs Sketch xorSW. Wir benötigen, wie im Kapitel Bildbearbeitung , zwei Methoden:
image(bild1,0,0);
bild2 = loadImage("bild2.bmp");
matrix1 = matrixVonBild(bild1);
matrix2 = matrixVonBild(bild2);
matrix3 = new int[w][h];
for(int i=0; i <h;i++){
for(int j=0; j <w;j++){
c1 = color(matrix1[i][j]);
c2 = color(matrix2[i][j]);
int a = 255 << 24;
int r = int(red(c1)) <<16;
int g = int(green(c1)) <<8;
int b = int(blue(c1));
int A = 255 <<24;
int R = int(red(c2)) << 16;
int G = int(green(c2)) <<8;
int B = int(blue(c2));
cBin1 = a | r | g | b;
cBin2 = A | R | G | B;
int aa = 255 << 24;
int rr = r ^ R;
int gg = g ^ G;
int bb = b ^ B;
cBin3 = aa | rr | gg | bb;
matrix3[i][j] = cBin3;
}
}
bild3 = bildVonMatrix(matrix3);
bild3.save("bild3.bmp");
Als letztes sollte die "Schlüsselempfindlichkeit" geprüft werden. Das ist schnell erledigt. In den Processing eigenen Funktionen wird mit float gearbeitet. Selbst wenn wir die Parameter als double-Werte anlegen, können wir uns nur auf sieben gültige Ziffern verlassen. Ändern Sie daher bei der Schlüsselerzeugung eine einzelne Ziffer bei einem der fünf Parameter im Bereich dieser ersten sieben Ziffern. Versuchen Sie nun das verschlüsselte Bild mit dem veränderten Schlüssel sichtbar zu machen. Das Ergebnis ist Chaos. Somit ist auch diese Forderung erfüllt.
Es gibt also 1035 verschiedene Schlüssel!
Es ist etwas umständlich mit zwei Tools zu arbeiten. Daher wird die Schlüsselerzeugung und die Ver/Ent-schlüsselung in einen Sketch gepackt: Sketch Schlüsselerzeugung und XOR-Verschlüsselung
Typisch Clifford-Attraktor: Mitunter bekommen Sie als Schlüssel kein Chaos-Bild, sondern eine wie auch immer geartete Struktur:
Dann haben Sie zufällig eine der seltenen Parameter-Kombination gefunden, die wir im Kapitel Clifford Attraktore mühsam gesucht haben. Eigentlich müsste man schluesselXOR.bmp nicht speichern. Es reicht während der Rechnung die Daten im Arbeitsspeicher zu haben. Damit man aber nicht versehentlich einen weniger chaotischen Schlüssel verwendet, sollt man das Bild anschauen. Es gibt aber, wie Sie sehen werden, noch einen zweiten Grund.
Wie sieht die Übergabe der Information konkret aus?
Nehmen wir an, Bob will Eve eine Nachricht zukommen lassen. Eve sollte den Schlüssel, bestehend aus fünf Parametern haben. Dann erzeugt sie sich den schluesselXOR.bmp mit dem Sketch, den sie beispielsweise hier runterladen kann und entschlüsselt damit das Bild bzw. die Nachricht im Bild.
Wie aber kommt der Schlüssel zu Eve? Sicher wäre, Bob und Eve träfen sich mindestens ein Mal, um die fünf Parameter festzulegen. Ein One-Time-Pad, das mit diesen Parametern erzeugt wird, darf aber nur ein einziges Mal verwendet werden. Müssen sie sich daher vor jeder Sendung einer verschlüsselten Nachricht treffen? Das wäre sinnlos! Dann könnten sie sich die Nachricht einfach sagen. Nein, ein Treffen genügt, denn jede verschlüsselte Nachricht enthält fortan auch die beim nächsten Mal zu verwendenten Parameter. Dieses Verfahren ist riskant, denn sollte es nur ein einziges Mal gelingen, die Verschlüsselung zu knacken, dann kann man zukünftig bequem mitlesen. Bisher gibt es ca. 1040 verschiedene Schlüssel. Machen wir 1080 daraus!
Permutation mit Clifford Attraktor
Die vier Bilder unten sind im Original jeweils 1200x1200 Pixel groß. Stellen Sie sich vor, Sie vertauschen
zufällig zwei Pixel, beginnend links oben und endend rechts unten. Ein Beispiel: Die Farbe des Pixel bei (345,129)
tauscht die Farben mit dem Pixel bei (24,954). Das wären in diesem Fall 1.44 Millionen Tauschvorgänge. Ein aktueller
Computer erledigt diese Aufgabe in 2 Sekunden. Kann man ein solches "Riesenpuzzle" mit Hilfe eines Computers wieder
in die ursprüngliche Form bringen?
Ja, kann man! Falls man die Tauschparameter gespeichert hat. Dann macht man, beginnend bei rechts unten und
endend links oben, alle Tauschaktionen wieder rückgängig. Dauert ebenfalls 2 Sekunden.
Und wie sieht es aus, wenn man diese Parameter nicht gespeichert hat? Versuchen wir, die Frage für ein sehr
kleines Bild, bestehend aus 16x16 Pixeln, zu beantworten. Nehmen wir weiter an, dass die Zahlenwerte von 1 bis
256 eingetragen sind. Die Zahlen stehen für die möglichen Grauwerte. Jeder Wert komme genau einmal vor.
Dann gibt es 256!, also etwa 10500 Möglichkeiten, die Zahlen bzw. Grauwerte zu verteilen. Noch Fragen?
Aber: Beim einem RGB-Farbbild gibt es mehr als 16 Millionen verschiedene Farbwerte. Wenn man nun ähnliche Werte kombiniert,
um damit versucht einen Bildteil zusammenzusetzen? Gute Idee, nur woher weiß ich, dass
das gefundene Bildsegment tatsächlich aus dem ursprünglichen Bild stammt? Was jedem sofort einleuchtet: Mit dem
Bild rechts neben der Provence-Landschaftsbild lassen sich unendlich viele sinnvolle Bilder zusammensetzten. Nicht überzeugt?
Dann verwenden wir ein Grau-Chaos-Bild als Quelle, um daraus durch Permutation ein anderes Grau-Chaos-Bild zu
erzeugen. Und genau das ist der Plan.
Zunächst erzeugen wir auf die gleiche Weise wie oben Clifford-Attraktor-Zufallszahlen. Allerdings doppelt so viele,
denn jeder Tausch benötigt zwei davon.
(Ist das Bild, wie bei uns, 1200x1200 Pixel groß, dann muss man in den
Einstellungen von Processing die Größe des zu verwendenden Arbeitsspeichers erhöhen -hier 8192 MB. Sollte
ihr Rechner zu wenig Speicher haben, muss die Bildgröße reduziert werden.)
Die Zufallszahlen wollen wir in
einer Textdatei speichern. Dazu muss man sie zunächst in einen String umformen. Wenn alle Zufallszahlen in
MatrixHisto[i][j] abgelegt sind, dann bekommt man zum Beispiel mit dieser Methode die
Umformung (Cols ist die doppelte Zahl der Spalten und rows die Anzahl der Zeilen des Bildes):
int[][] MatrixHisto = matrix;
String[]schluessel = new String[n];
for(int i = 0; i < Cols ; i++){
for(int j = 0; j < rows; j++){
String x = str(round(MatrixHisto[i][j])% cols);
schluessel[i + j*Cols] = x;
}
}
return schluessel; }
for(int j=0;j<rows;j++){
int nummer = 2*(i+j*cols);
ax=Integer.parseInt(permSchluessel[nummer]);
ay=Integer.parseInt(permSchluessel[nummer+1]);
bx=i;by=j;
tauschA = bildErgebnis.get(ax,ay);
tauschB = bildErgebnis.get(bx,by);
bildErgebnis.set(ax,ay,tauschB) ;
bildErgebnis.set(bx,by,tauschA) ;
}
}
Bleibt die Frage: Ist der Schlüssel, wie im xor-Fall, empfindlich für kleine Änderungen in den Parametern? Das lässt sich einfach überprüfen: Verschlüsseln sie ein Bild mit fünf Paramtern, die jeweils aus acht Ziffern bestehen. Erzeugen Sie einen neuen Text-Schlüssel schluessel[], wobei nur eine Ziffer eines Parameters geändert wurde. Versuchen Sie nun damit das verschlüsselte Bild wieder zu entschlüsseln. Das Ergebnis ist Chaos! Es gibt daher auch hier 1040 verschiedene Schlüssel. Insgesamt also 1040x1040 = 1080, sofern man für beide Vorgänge verschiedene Parameter wählt.
Wie sieht nun der gesamte Ver/Entschlüsselungsprozess aus?
Einmal müssen sich Bob und Eve treffen, um ihre ersten 10 Paramter festzulegen. Danach ist kein Kontakt mehr nötig. Nun möchte Bob eine geheime Nachricht an Eve schicken. Bob verschlüsselt das Bild / den Text zuerst mit der ersten Methode (xor) und danach mit der zweiten (Permutation). Auf dem Bild befinden sich auch die beim nächsten Mal zu verwendeten zehn Paramter. Eve entschlüsselt das Bild zunächst mit der Permutationsmethode und danach mit xor. Sie notiert sich die neuen Parameter. Vorausgesetzt, ihre Computer sind nicht kompromettiert, dann ist die Nachricht auch mit Quantencomputer nicht zu entschlüsseln.
(Übrigens, die Anzahl der Atome im Universum liegt zwischen 1084 und 1089)
Es ist umständlich, mit zwei Programmen zu arbeiten. Versuchen Sie, die beiden Sketche in einem Sketch zu realisieren. Es soll am Ende nur noch drei Aktionen geben: "Schlüssel erzeugen", "verschlüsseln" und "entschlüsseln", so dass der Anwender von der doppelten Ver/Entschlüsselung nichts bemerkt. Das Ergebnis können Sie hier runterladen.
Noch immer ist die Anwendung nicht perfekt: Man benötigt den Processing-Editor und man muss die Parameter in den Quelltext eingeben. Etwa in dieser Form:
Wie das funktioniert erfahren Sie hier !
Sketch Farbe mit XOR verschlüsseln
Sketch Clifford Attraktor Schlüssel
Sketch SW-Bild verschlüsseln mit XOR
Sketch Schlüsselerzeugung und XOR-Verschlüsselung
Sketch Schlüsselerzeugung und Permutation
Sketch XOR und Permutation
Menu