Maps
Standard Map: Fluchtdiagramm
Mit Hilfe der Trajektorien haben wir einen recht guten Eindruck über die Natur der Standardmap bekommen. Dennoch
bleiben Zweifel, ob man nicht noch weitere Erkenntnisse gewinnen könnte, indem man die Methode der Untersuchung
ändert. Vergleichen kann man das mit einer ärztlichen Untersuchung zunächst mit Röntenstrahlen und dann, weil das
Ergebnis nicht eindeutig ist, mit einer Magnetresonanztomographie.
Wenn Sie das Buch studiert haben,wissen Sie, was "Fluchtdiagramme" sind. Das bekannteste Beispiel ist die
fraktale Mandelbrot-Menge. Die Farbe, die man einem Punkt der Definitionsmenge zuordnet, wird durch die "Geschwindigkeit"
bestimmt, mit der sich der Punkt bei der Iteration von seinem Ursprungort wegbewegt. Im Fall der Standardmap
interpretieren wir die "Geschwindigkeit" zunächst dadurch, dass wie den maximalen y-Abstand (also in der Senkrechten) zweier
Punkte bei 50 Iterationen berechnen. Und diesem Wert ordnen wir eine Farbe zu. Probieren Sie es aus!
Mit Klick in das Bild werden die Trajektorien weiß eingetragen.
Klickt man zuvor auf die Taste V, dann bewirkt ein Klick in das Bild ein Zoomen an dieser Stelle.
Im nachfolgenden Bild wurde zwei Mal vergrößert und danach einige Trajektoren eingezeichnet:
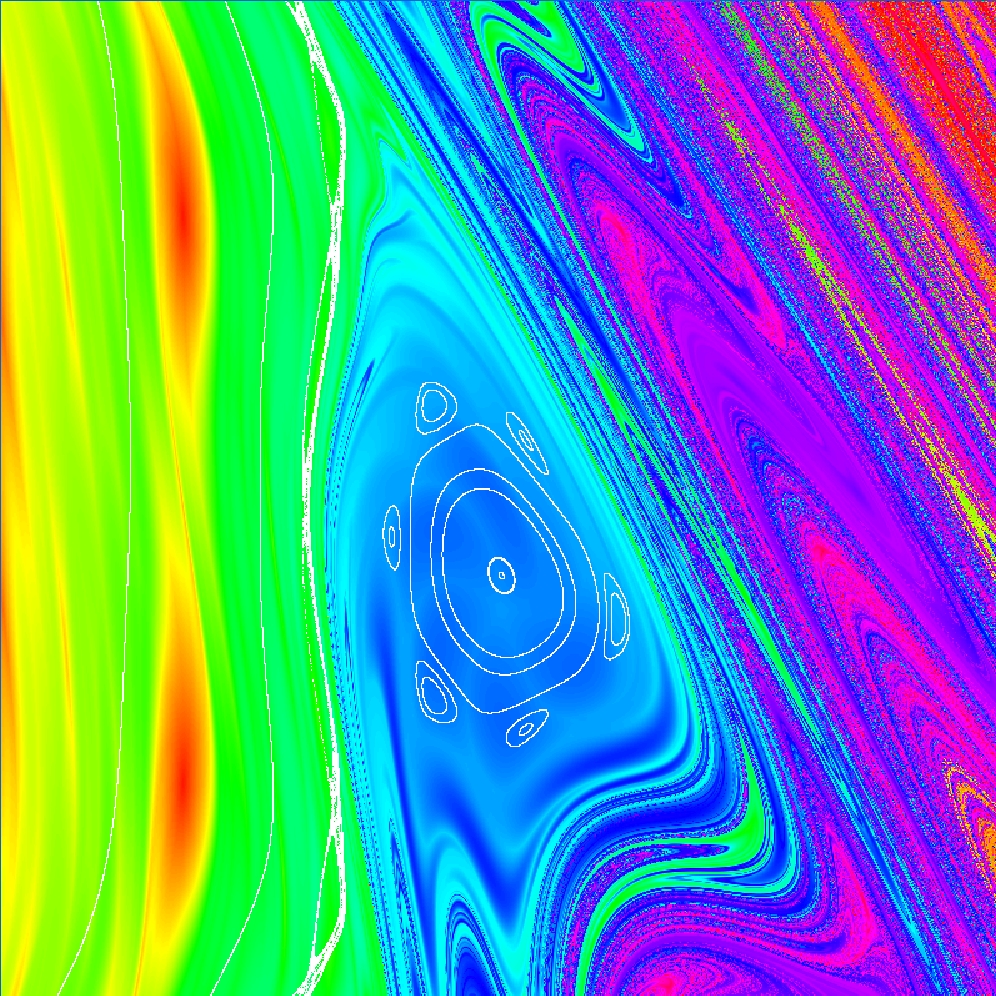
Im Bild links unten wurde ein Ausschnitt der Standartmap vergrößert. Sie sehen, dass viele Startpunkte
verwendet wurden. Dennoch erkennt man im mittleren Bereich des rot umrandeten Bildsegments nur Chaos.
Der grün umrandete Bereich daneben zeigt den selben Ausschnitt - allerdings im Fluchtdiagramm, bei dem (wie oben)
der maximale y-Abstand bei 50 Iterationen farblich codiert wurde. Aber hier ist ganz deutlich eine Struktur
zu erkennen. (Im Abschnitt Hufeisen suchen haben wir uns
etwas ausführlicher mit dieser Eigenschaft beschäftigt.)
Suchen Sie den Bereich im obigen Sketch und vergrößern Sie diesen noch stärker, so etwa, wie in der Vergrößerung
des grünen Rahmens weiter rechts.
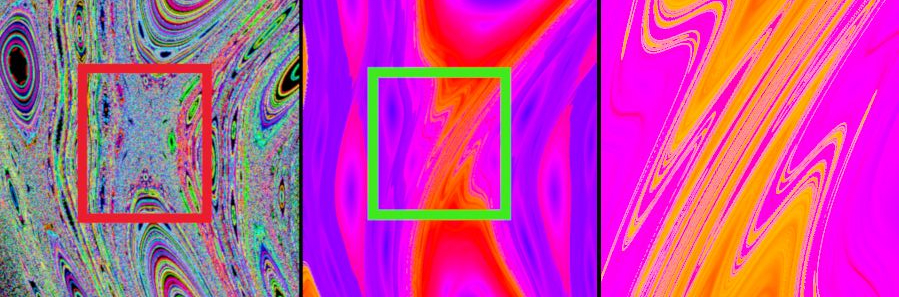
Sie erinnern sich: Das obige Fluchtdiagramm wurde über den maximalen y-Abstand errechnet. Es gibt natürlich noch
viele andere Möglichkeiten, das Verhalten der Iterationspunkte zu codieren. Man könnte beispielsweise den Abstand
der ersten Punktes vom letzten verwenden oder den Durchschnitt der Abstände zweier aufeinander folgender Punkte
oder....- der Phantasie sind hier keine Grenzen gesetzt.
Die letzten sechs Bilder sind Ergebnisse derartiger Experimente. Sie können sich die Sketche, mit denen sie
erzeugt wurden am Ende runterladen.
Beachten Sie dabei: Im Gegensatz zu dem obigen, im Browser laufenden Sketch, bei dem Multithreading leider
nicht funktioniert, sind die herunterladbaren Sketche tatsächlich so programmiert, dass jeder Core des Prozessors
die Berechnung eines Teils des Bildes übernimmt. Bei 16 Core etwa benötigt die Berechnung nur noch etwa ein Zwölftel
der Zeit.

Gesondert soll hier auch ein Fluchtdiagramm in Polarkoordinaten behandelt werden. Insbesonder der rätselhafte Fixpunkt bei (0;0), der eigentlich sowohl elliptisch als auch hyperbolisch sein sollte, zeigt hier deutlich mehr Struktur, als in der Zylinder- bzw. Torusdarstellung. (Bild unten links).
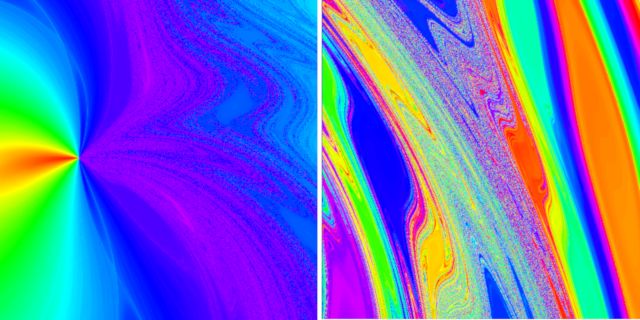
Fluchtdiagramm 1
Fluchtdiagramm 2
Fluchtdiagramm 3
Fluchtdiagramm 4
Fluchtdiagramm 5
Fluchtdiagramm 6
Menu