Maps

Standard Map: Suche nach Hufeisen - Mannigfaltigkeiten


Alle im Folgenden gezeigten Bilder können Sie interaktiv hier selbst erzeugen.


Im Bild oben sehen Sie eine auf den Ursprung (0;0) zentrierte (zylindrische) Standardabbildung mit K = 1,7. Links werden die üblichen Trajektorien angezeigt und rechts das zugehörige Fluchtdiagramm.

Der rot markierte Ursprung ist, wie man leicht nachprüfen kann, ein Fixpunkt erster Ordnung. Es fällt auf, dass die Trajektorien bei diesem Fixpunkt nur Chaos zeigen. Ganz anders beim Fluchtdiagramm. Hier sind sinusartige Schwingungen zu sehen, die sich hier nur verraten, weil Nachbarpunkte auf einer der Linie ganz offensichtlich ein ähnliches Fluchtverhalten zeigen. (Es gibt, wie im Kapitel Fluchtdiagramme behandelt, ganz verschiedene Arten, die "Flucht" der Punkte bei der Iteration zu messen. Hier wurde einfach der Abstand des kleinsten vom größten y-Wert genutzt.)
Zugegeben, die Standardabbildung macht es uns nicht leicht, die Umgebung des Fixpunktes (0;0) zu untersuchen. Daher verwenden wir dort mit Hilfe der Jacobi-Matrix eine lineare Näherung der Standardabbildung. Das geht gut, wenn wir nur eine sehr kleine Umgebung des Fixpunktes betrachten. Hier sind die mathematischen Grundlagen:

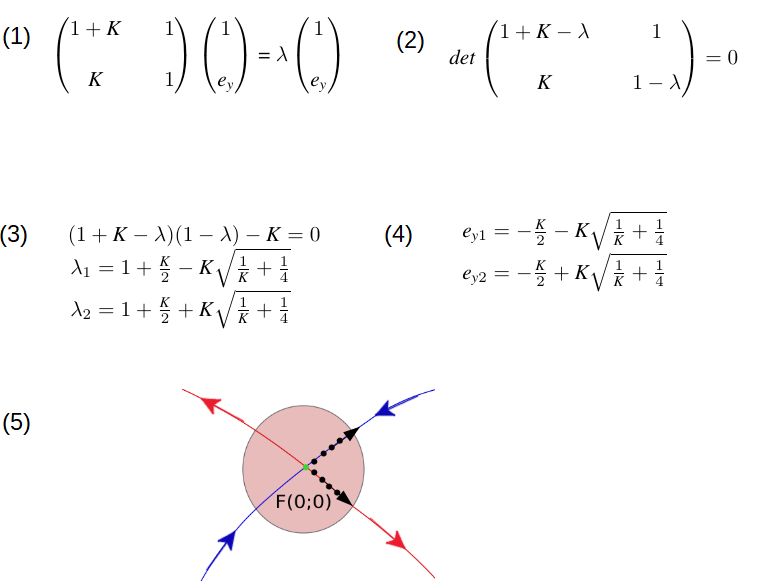
Die Matrix (1) ist die Jakobi-Matrix für α = 0. Es wird mit dieser Gleichung versucht, sogenannte "Eigenvektoren" der Abbildung zu finden. Die reelle Zahl λ nennt man dann den "Eigenwert" zum Eigenvektor. Da es auf die Länge des Eigenvektors nicht ankommt, wurde hier die erste Komponente auf 1 normiert. Die Rechnung muss uns also ey liefern.
Mit (2) bekommen wir zunächst eine Gleichung für eventuelle Eigenwerte λ. Die zu lösende Gleichung und die beiden Lösungen sind in (3) zu sehen. In (4) schließlich sind die 2.Komponente der Einheitsvektoren angegeben. Wie Sie sehen, gibt es für K>-4 zwei Lösungen.
Für beispielsweise K =1,7 ist λ 1 = 3,4064 und λ 2 = 0,2936. Das bedeutet, dass alle Punkte, die auf dem zu λ 1 zugehörigen Eigenvektor liegen, sich bei der Iteration vom Fixpunkt wegbewegen. Genau umgekehrt verhält es sich bei den Punkten, die auf dem zu λ 2 gehörigen Eigenvektor befinden. Sie nähern sich dem Fixpunkt immer mehr an. In (5) wird darüber hinaus angedeutet, wie die Rechnung ablaufen wird: Für eine "hinreichend kleine Umgebung" des Fixpunktes sorgen wir, indem wir die Eigenvektoren auf ein Tausendstel ihrer ursprünglichen Länge kürzen. Auf diesen verkürzten Vektoren bringen wir auf beide Seiten 50 000 Punkte unter. Kein Problem, wenn man mit double-Attributen arbeitet! Will man allerdings auch im Fall von λ 2 = 0,2936 mehr Informationen, als die bloße Annäherung an den Fixpunkt, muss man diese Punkte "rückwärts" iterieren, also die Umkehrabbildung verwenden. Das Ergebnis der Rechnung zeigen die folgenden Bilder:


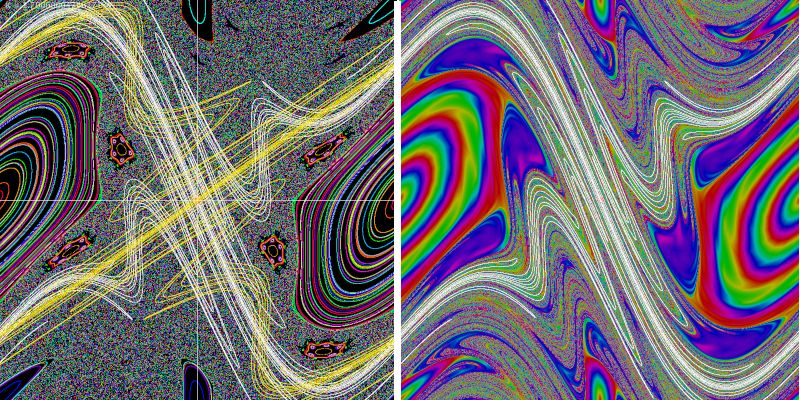
Weiß sind die (dreizehn mal) rückwärts iterierten Punkte auf dem Eigenvektor mit λ 2. Gelb zeigt die (ebenfalls dreizehn mal) vorwärts iterierten Punkte auf dem Eigenvektor mit λ1 . Im Bild rechts wurden die weißen Punkte, die man auch auf der linken Seite sieht, in das zugehörige Fluchtdiagramm eingetragen. Nun können Sie verstehen, weshalb das Fluchtdiagramm diese merkwürdigen Formen angezeigt hat. Schauen wir uns die Sache etwas genauer an:


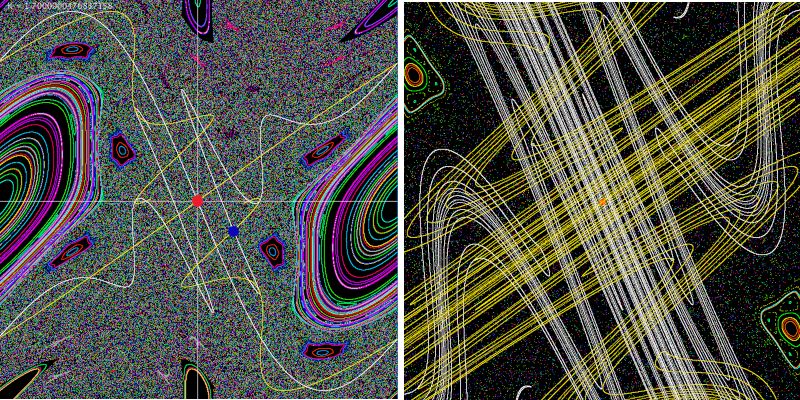
Im linken Bild wurden die Punkte auf den Eigenvektoren nur wenige Male iteriert. Dadurch sind die Linien kürzer und man bekommt daher einen etwas besseren Überblick. Den rot markierten hyperbolischen Fixpunkt kann man sich als Gebirgspass vorstellen. Eine Kugel würde sich auf den weißen Linien "bergab" vom Fixpunkt entfernen. Befindet sich die Kugel auf einer gelben Linie, so rollt sie zum Fixpunkt. Die durch die gelben Punkte markierte Punktemenge nennt man stabile Mannigfaltigkeit, die weißen Punkte liegen auf einer instabilen Mannigfaltigkeit. Die blaue Markierung, auf der sich die beiden Mannigfaltigkeiten schneiden, wird homokliner Punkt genannt. In der Vergrößerung im rechten Bild, diesmal mit deutlich mehr Iterationen, kann man erkennen, dass es unglaublich viele solche homokliner Punkte geben muss. Dass sich aber die beiden Mannigfaltigkeiten selbst schneiden, ist nirgends zu sehen.

Um eine brauchbare Übersicht zu bekommen, wurden im Bild links die Punkte auf den Eigenvektoren nur wenige Male iteriert. (Die Punkte auf den um 1800 gedrehten Eigenvektoren werden weggelassen.) Die Pfeile zeigen die Richtung an, in der die Punkte durch die Stanardabbildung bewegt werden. Beachten Sie, dass es sich bei dem Bild um eine Zylinder Oberfläche handelt. Die instabile Mannigfaltigkeit (gelb), die am Fixpunkt (rot) startet und oben rechts am Rand ankommt, geht auf der linken Seite auf gleicher Höhe weiter. Die Punktemenge der instabilen aber auch der stabilen Mannigfaltigkeit wird homokliner Orbitgenannt.
Nun wird es Zeit, einige wichtige Sätze über homokline Orbits festzuhalten.
Ein homokliner Orbit kann sich niemals selbst schneiden.
Das liegt ganz einfach daran, dass die Standardabbildung umkehrbar ist. Gäbe es einen Schnittpunkt, dann wäre die Funktion an dieser Stelle nicht mehr eindeutig.
Die Mannigfaltigkeiten sind invariante Linien der Standardabbildung.
Das bedeutet nichs anderes, als dass jeder Punkt auf einer der Mannigfaltigkeiten nach der Abbildung gemäß der Definition wieder auf ihr landet.
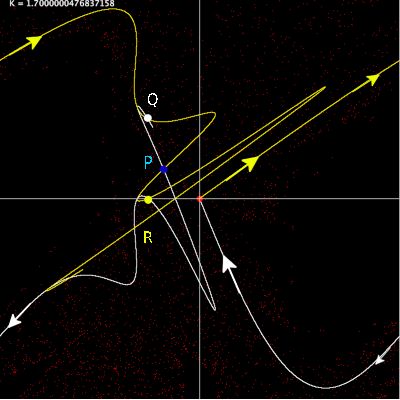
Sehen Sie sich den blau markierten Schnittpunkt P der instabilen mit der stabilen Mannigfaltigkeit an. Man nennt derartige Schnittpunkte homokline Punkte.
Gibt es einen homoklinen Punkt, dann gibt es unendlich viele.
Da P als homokliner Punkt kein Fixpunkt sein kann, muss das Bild f(P) aber auch f-1(P) wegen der Stetigkeit von f und f-1 wieder an anderer Stelle auf beiden Mannigfaltigkeiten liegen. Diese neuen homoklinen Punkte bedingen aber nun jeweils einen weiteren homokline Punkte. Somit ist die Anzahl derartiger Punkte nicht beschränkt. Ganz konkret kann man im Bild oben sagen, dass wegen der orientierungstreue der Standardabbildung erst der übernächste Schnittpunkt Bildpunkt sein kann. Das heißt: f(P) = Q bzw. f-1(P) = R. Und noch etwas ist klar: Obwohl fn(P) und f-n(P) sich dem Fixpunkt immer mehr nähern, werden sie ihn nie erreichen, sich auf dem Weg dahin aber unendlich oft schneiden.


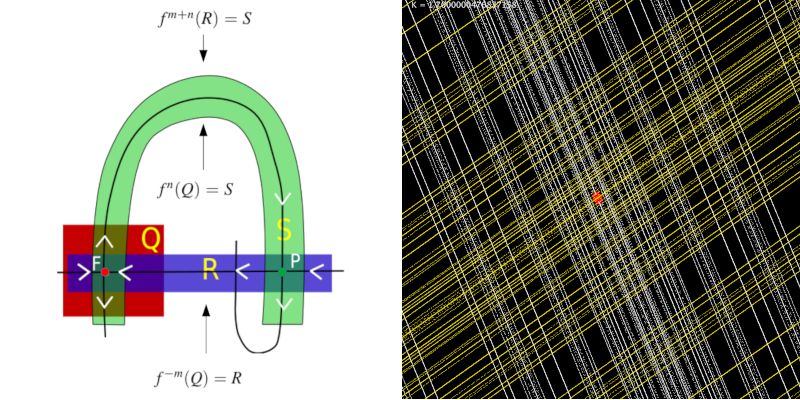
Was hat nun ein hyperbolischer Fixpunkt mit einer Hufeisenabbildung zu tun? Eine erste Idee liefert das idealisierte Bild oben links. Der Fixpunkt F liegt auf dem Rechteck Q; es gibt einen homoklinen Punkt P, der auf beiden Mannigfaltigkeiten liegt. Bildet man das Rechteck Q oft genug, also zum Beispiel m mal mit der Umkehrabbildung der Standard Map f-1 ab, dann wird das Bild R von Q den Punkt P enthalten. Analog gilt, dass sofern man Q oft genug mit f abbildet (zum Beispiel n mal), dann wird das Bild S Punkt P ebenfalls enthalten. Nimmt man jetzt R als Definitionsmenge und betrachtet die Abbildung fm+n, dann wird aus dem Rechteck R das "Hufeisen" S. Das Bild ist, wie geschrieben, idealisiert. Wie man weiter unten sehen kann, sieht das Bild eines Rechtecks nicht wirklich wie ein Hufeisen aus. Das ändert aber nichts daran, dass der Gedanke topologisch gesehen korrekt ist.
Im Bild links daneben wurde die Umbebung des Fixpunktes so stark vergrößert, dass der Bildausschnitt in etwa den Bereich zeigt, der zwei Bilder weiter oben (rechts) durch die rote Markierung des Fixpunktes überdeckt wird. Es wurden 2 Millionen Punkte auf den Eigenvektoren plaziert und dann 16 mal iteriert. Drehen Sie das Bild gedanklich um ca. 45o, dann ähnelt es doch sehr der Erzeugung des Cantor-Staubes in der Hufeisenabbildung. Schauen wir uns also einfach mal an, was wirklich passiert, wenn man ein Rechteck n mal vorwärts und ebenfalls n mal rückwärts iteriert.


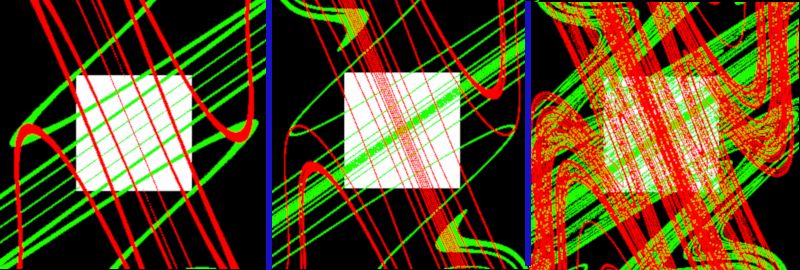
Von links nach rechts nimmt die Anzahl n der Iterationen mit Standardabbildung f bzw. f-1 zu. Grün zeigt die Abbildung des weißen Rechtecks mit f, rot die Abbildung mit f-1. Wenn man die Bereiche, an denen sich die roten mit den grünen Flächen auf dem Rechteck schneiden, dann weiß man, dass dort die Fixpunkte von fn+n zu finden sind. Genau wie bei der Horseshoe-Abbildung wird die Anzahl der Schnittflächen exponentiell wachsen und gleichzeitig immer weniger Fläche besitzen. Die Gesamtfläche der Schnitte geht mit wachsender Anzahl der Iterationen gegen Null, wie beim Cantor-Staub, der reines Chaos anzeigt...

Nochmals zur Erinnerung: Alle gezeigten Bilder können Sie interaktiv hier selbst erzeugen.

Da wäre noch eine Kleinigkeit: Erinnern Sie sich an die Polarkoordinaten Darstellung der Standardabbildung? Auch hier ist der Punkt (0,0) ganz ohne Zweifel ein Fixpunkt. Die erste Koordinate steht für den Winkel, die zweite für den Radius. Bleibt die Frage: Ist das ein elliptischer oder ein hypberbolischer Fixpunkt? Im Bild unten wurde der Fixpunkt markiert. Was wir sehen verwirrt zunächst. Es gibt einen Teil der Umgebung, die für einen elliptischen Fixpunkt spricht, aber auch ein deutlich kleineren Teil rechts, bei dem man für hyperbolischen Fixpunkt votieren würde.


Die Frage ist allerdings sinnlos, denn im Punkt (0;0) ist die Abbildung nicht umkehrbar. Wenn der Radius Null ist, dann kann man ihm alle Winkel zuordnen. Und damit ist die Vorausetzung für unsere bisher gefundenen Erkenntnisse nicht erfüllt. Dennoch es es möglich, auch hier zwei Mannigfaltigkeiten anzugeben:


Das zugehörige Programm können Sie für weitere Studien hier runterladen:

Sketch StandardMapHufeisen

Sketch StandardMapPolarkoordinatenMF

Menu