Maps

Standard Map


"Map" ist der englische Ausdruck für "Abbildung". Unser Thema klingt nun recht bedeutungsvoll: Standardabbildung oder noch genauer Tschirikow-Tayler-Standardabbildung.
Es gibt physikalische System, die man auf recht einfache Weise simulieren kann. Die zugehörigen Differentialgleichungen sind exakt lösbar und liefern Gleichungen, mit deren Hilfe man bei bekannter Startbedingung den Zustand des Systems in der Zukunft aber auch in der Vergangenheit berechnen kann. Ein typisches Beipiel sind die Keplerschen Gesetze. Sie erlauben in guter Näherung den Umlauf eines Planeten um die Sonne zu berechnen. Exakt sind die Werte allerdings nicht, denn man vernachlässigt die Wirkung der Planeten untereinander. Das Zweikörper-Problem ist ein integrables Hamilton System, aber schon beim Dreikörper-Problem kann Chaos entstehen und man hat es mit einem nicht-linearen und nicht-integrablem Hamilton System zu tun. Wie beim Doppelpendel kann man dann nur versuchen, mit Hilfe zum Beispiel der Runge-Kutta-Methode eine Näherung zu berechnen.
Gibt es vielleicht ein einfacheres chaotische Systeme, als Doppelpendel oder Dreikörper-Problem?

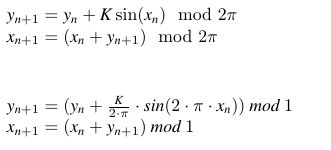
Der nebenstehende Abbildungsvorschrift eines Quadrats (der Seitenlänge oben: 2 π unten: 1 ) auf sich selbst - oder gleichbedeutend der Oberfläche eines S2 Torus auf sich selbst - sieht man ihre Bedeutung nicht an. Aber schon der Name "Standardabbildung" lässt vermuten, dass hiermit etwas Wesentliches ausgedrückt wird. Zum einen kann man mit ihrer Hilfe zu einem Punkt des Phasenraums (auf dem Poincaré-Schnitt) eines periodisch angestoßenen Rotator den Folgepunkt berechnen. Und dies ganz ohne Differenzialgleichungen zu lösen.
Das wäre nicht sonderlich aufregend, denn der Kicked Rotator hat ja im täglichen Leben keine besondere Bedeutung. Aber mit Hilfe dieser Abbildung können viele Probleme aus Quantenphysik, Plasmaphysik, Astrophysik, Festkörpberphysik und sogar der Meteorologie modelliert werden. Allen gemeinsam ist die Frage: Wann wird ein System chaotisch. Oder anders ausgedrückt: Ist das System bei kleinen Störungen stabil?
(Hinweis: x steht beim Kicked Rotator für den Winkel und y für die Winkelgeschwindigkeit.)


Wenn Ihnen die Begriffe "Runge-Kutta-Methode" oder "Poincaré-Schnitt" nicht vertraut sind, dann wäre es hilfreich, wenn Sie zunächst das Kapitel Wege ins Chaos durchlesen.

Im folgenden Sketch bekommen Sie einen ersten Eindruck, wie die Standard-Map für wachsenden Störungs-Parameter K aussehen kann. Beobachten Sie, wie das Chaos allmählich zunimmt. Nach rechts ist der Winkel und nach oben die Winkelgeschwindigkeit eingetragen.
Der erste Wert für den Störungsparameter K ist 0.5. Wenn Sie auf das Bild klicken, wird K jeweils um 0.05 erhöht. So können Sie bis zu K = 5 die Zunahme des Chaos beobachten. Achten Sie besonders auch darauf, wie sich die geschlossenen Linien dabei verändern.


Der obige Sketch lässt einem nur eine Möglichkeit: Die Störungsvariable K durch Mausklick um 0.5 zu erhöhen. Das mag ausreichend sein für einen ersten Eindruck. Es reicht jedoch nicht, um die Details zu sehen. Man sollte zoomen können, einzelne Trajektorien hervorheben und vor allem durch eigene Aktionen das beobachten können, was einen gerade interessiert. Hier nochmal die Namen für die verschiedenen Objekte:

Die ellipsenförmigen geschlossenen Linien um die elliptischen Fixpunkte zeigen sogenannte "quasiperiodische" Bewegungen an.

Unten ein Beispiel für die Vergrößerung bis zum Faktor 10 000. Wenn Sie eigene Experimente mit der Standard Map machen wollen, klicken Sie auf diesen Link zum Standartmap Sketch
.


Auf der Seite Standard Map: Überblick können Sie selbst Hand anlegen.

Das Hauptinteresse an der Standard Map ist zweifelsohne die Möglichkeit, in bestimmten Fällen Aussagen über die Stabilität eines dynamischen Systems zu machen. Bleibt beispielsweise unsere Erde auch in den nächsten Jahrhunderten noch auf ihrer Bahn oder wird die Wirkung des Planeten Jupiters so groß, dass sie aus dem Sonnensystem geschleudert wird? Dass man überhaupt über ein solches Szenario nachdenkt, mag weit hergeholt erscheinen. In Wahrheit weiß man aber erst seit dem letzten Jahrhundert, dass dies auch in vielen Millionen Jahren nicht der Fall sein wird. Und hier kommen die KAM-Tori ins Spiel. Sie erinnern sich, dass die periodischen Bewegungen im Poincaré-Schnitt lediglich aus einem Punkt bestehen. Jeder dieser periodischen Bewegungen war eine Schwingungszahl zugeordnet. Die ellipsenförmigen Bahnen (Orbits) um den Punkt herum, beschreiben, wie schon erwähnt, quasiperiodische Bewegungen zu eben dieser Periode.
Die KAM-Tori besitzen eine irrationale Schwingungszahl. Das KAM-Theorem besagt ja in der Umkehrung, dass periodische Schwingungen nicht sonderlich stabil sind. Es zeigt sich, dass sie um so weniger stabil sind, je kleiner der Nenner der (gekürzten) Schwingungszahl ist. Stabil hingegen sind die KAM-Tori, denn deren Schwingungszahlen sind irrational und lassen sich daher nur durch rationale Brüche annähern. Je genau man sie aber durch Brüche annähern will, desto größer werden die zugehörigen Nenner. Daraus lässt sich folgern, dass die KAM-Tori recht resistent gegen Störungen sind.
Wenn Sie dazu eigene Experimente machen wollen, dann wäre der Abschnitt KAM- und Can-Torus etwas für Sie.

Im Abschnitt Fixpunkte haben Sie erfahren, dass jede Serie elliptischer Fixpunkte zu einer bestimmten Schwingungszahl immer mindestens einen Fixpunkt auf x = 0.5 haben muss. Es wäre daher doch interessant, bei eben diesem x-Wert einen Schnitt durch die Map zu machen und für alle Punkte (0.5,y) die Neigung zu Chaos an diesem Punkt zu untersuchen. Das Werkzeug dazu haben wir bereits. Mit dem Lyapunov-Exponent haben wir bereits gearbeitet. Die Idee: Für alle y-Werte nimmt man einen Nachbar ganz in der Nähe. Man bekommt so zwei Punkte (0.5,y) und (0.5,y+d), mit zum Beispiel d = 0.0001. Dann iteriert man beide Punkte vielleicht 1000 mal, ohne weitere Rechnung. Und ab 1000 bis vielleict 5000 berechnet man den Abstand, den beide Punkte dann zueinander haben.



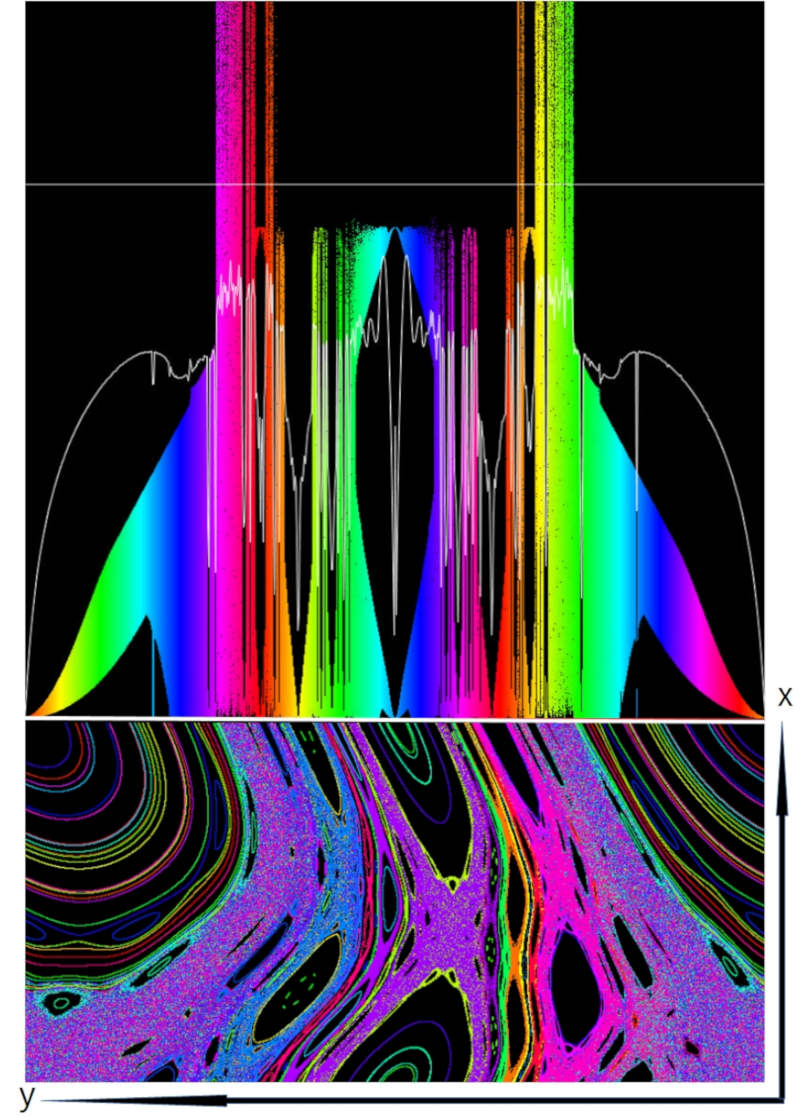
In der obigen Darstellung wurde das Bild der Stanard Map um 90 Grad gegen den Uhrzeigersinn gedreht und genau bei x = 0.5 das Ergebnis des Lyapunov-Exponenten (weiße Linie) angehängt. Wenn Sie mehr dazu erfahren wollen und/oder das Programm selbst testen wollen, dann schauen Sie sich den Abschnitt Standard Map: Lyapunov-Test an.



Standard Map K wachsend .

Menu