Maps
Standard Map: Lyapunov-Test
Kann man die chaotischen Bereiche der Standardabbildung nicht noch auf eine elegantere Art eingrenzen? Falls Sie mit dem Lyapunov-Exponent bereits gearbeitet haben, fällt Ihnen möglicherweise ein, dass mit diesem Verfahren im eindimensionalen Fall sehr genau festgestellt werden kann, wo Chaos herrscht und wo nicht. Leider ist die Standardabbildung zweidimensional. Aber ließe sich nicht mit Hilfe partieller Abbleitungen ein Schnitt erzeugen, der entweder x oder y kontant hält?
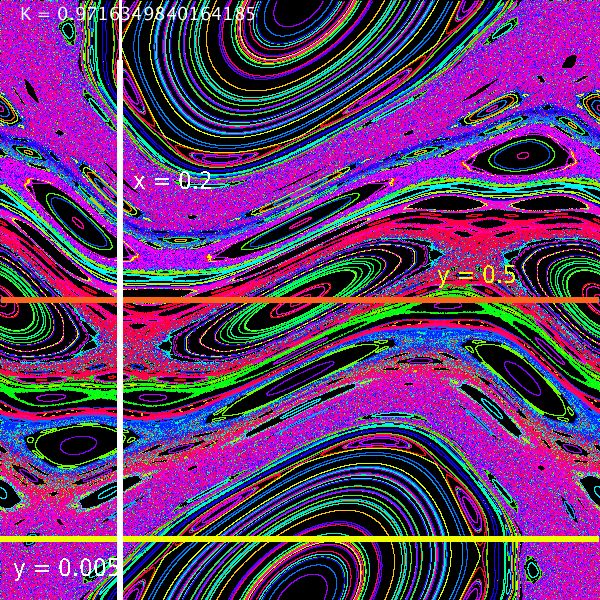
Im obigen Bild (normierte Torus-Darstellung) sind drei Schnitte markiert: Der weiße y-Schnitt bei x = 0.2,
der orange x-Schnitt bei y = 0.5 und der gelbe x-Schnitt bei y =0.05.
Leider versagt hier wegen der Zweidimenionalität die elegante Form des
Lyapunov-Verfahrens .
Dort musste man lediglich in allen Werten der Iteration die Ableitung bilden, logarithmieren und zum Schluss den
Durchschnitt bilden. Das Problem besteht nicht darin, dass man die partiellen Ableitungen nicht bilden könnte.
Stellen Sie sich einen y-Schnitt mit konstantem x0 vor. Im nächsten Iterations-Schritt ist
x0 sehr wahrscheinlich verändert. Was tun? Man könnte auf die Idee kommen, die Änderung in x0
rückgängig zu machen, also lediglich auf die Veränderung in y zu schauen. Probieren Sie es aus!
Sie werden feststellen, dass alle Ableitungen nach y mit konstantem x0 ebenfalls konstant sind.
Nein, was wirklich hilft, ist sich die ursprüngliche Definition des Lyapunov-Exponenten anzuschauen:
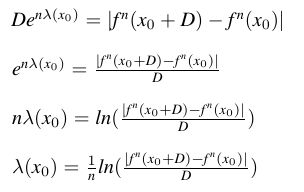
Der anfängliche Fehler D wächst exponentiell. Das Wachstum ist abhängig vom Startwert x0 und von der
Anzahl der Iterationen n. Kennt man den Exponenten λ, so kann man mit Hilfe des Vorzeichens von λ
bestimmen, ob Chaos oder Ordnung vorliegt. Über den Betrag von λ kann man "Stärke" von Chaos bzw.
Ordnung definieren.
Betrachten wir einen x-Schnitt bei y = 0.05 (blaue Linie im Bild oben) und schauen uns die Situation mit Startwerten
(x0 ; 0.05) und (x0+D ; 0.05) an.
Wie Sie an der Endformel erkennen können, werden beide Werte n mal iteriert.
Die Ergebnisse werden subtrahiert und durch D dividiert. Als letzter Schritt muss der Betrag des Ergebnisses
noch logarithmiert und durch die Anzahl der Iterationen geteilt werden.
Das so gewonnene Schaubild λ(x) wurde im folgenden Bild direkt über den x-Schnitt gezeichnet. Man kann
deutlich erkennen, dass negative λ (und λ=0) offensichtlich genau in elliptischen oder
hyperbolischen Fixpunkten angenommen werden. Weiterhin sieht man, das "größeres Chaos" mit größerem λ
einhergeht.
Wir beschränken uns im folgenden Sketch nicht auf das Anzeigen des Lyapunov-Exponenten.
Vielmehr werden über dem aktuellen x0 alle Abstände bis zum Erreichen der Schranke n farbig
eingetragen. (Im Fenster unten gilt: Je höher die Linie, desto mehr Iterationen sind nötig, um die
Schranke zu erreichen.) Die grauen Bereiche wurden
mit dem Faktor 20000 im Vergleich zu den bunten Eintragungen multipliziert, um sie überhaupt sehen zu können.
Dargestellt wird ein x-Schnitt mit y = 0.2 und Störungsfaktor K = 1.3. Mit einem Klick
können Sie dafür sorgen, dass an eben dieser Stelle mit Faktor 5 gezoomt wird (zoomen lediglich bezogen auf x).

Für allen weiteren Operationen wählen
Sie eine der folgenden Taste:
+-Taste: Der Störungsfaktor K wird um 0.1 erhöht.
--Taste: Der Störungsfaktor K wird um 0.1 verringert.
p-Taste: Der Wert y des x-Schnitts wird um 0.02 erhöht.
m-Taste: Der Wert y des x-Schnitts wird um 0.02 verringert.
1-Taste: Die Anzahl der Iterationen n wird um 1000 vergrößert.
2-Taste: Die Anzahl der Iterationen n wird um 1000 verringert.
So hübsch die senkrechten bunten Linien anzuschauen sind, einen echten Mehrwert an Information liefern sie
nur in bescheidenem Maß. Außerdem kann man immer nur den x-Schnitt für ein festes y ansehen. Daher werden wir
nun in ähnlicher Weise wie bei den
Fluchtdiagrammen vorgehen.
Die Farbe des Pixels mit den Bild-Koordinaten (i,j) bekommt man, indem man zunächst die zu (i,j) gehörigen
Koordinaten (x,y) berechnet und für diese Koordinaten den Wert von λ im x-Schnitt bestimmt.
Weil die Differenzierung zwischen den einzelnen Werten von λ nicht all zu groß ist, berechnen wir
stattdessen den Mittelwert aller λ ab einem Startwert Z bis zum Endwert n. Es gibt
hierzu zwei Programme: Den Single- und den Mulit-Thread Lypunov-Fraktal Sketch. Der Rechenaufwand ist erheblich!
Wenn Sie also mehrere Prozessor-Core haben, verwenden Sie den Multi-Thread Sketch. (Bei 16 Core beispielsweise ist die
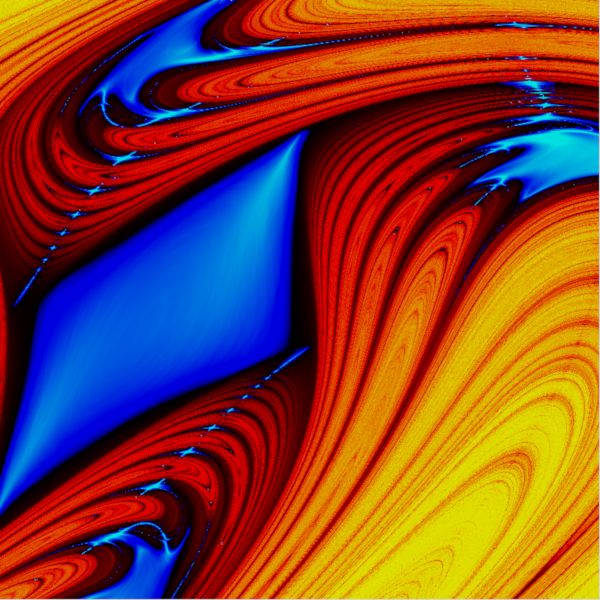
Rechenzeit etwa ein Zwölftel der Zeit wie beim Single-Thread.) Beim ersten Bild (normierte Form) ist der
Punkt links unten (0;0) und der Punkt rechts oben (1;1). Darunter sehen Sie einen 125-fache vergrößerten
Bildauschnitt. Die Farbkodierung geht in Bereichen der Ordnung bzw. des schwachen Chaos (λ < 7) von
dunkelblau nach türkis.
In Bereichen des Chaos (λ > 7) von rot nach gelb. Die Grenze für λ, hier den Wert 7, findet
man durch probieren. Ein KAM-Torus wäre im blauen Bereich zu finden. Da wir hier K = 0,97 gewählt haben, sollte
sich eine durchgehende Linie im blauen Bereich finden lassen. Testen Sie K = 1: Hier sucht man vergeblich.
Mit einem Rechtsklick wird die angeklickte Stelle 5-fach vergrößert. Linksklick mit +-Taste vergrößert
den Störungsfaktor K um 0.05.

Dass wir mit der oben dargestellten "x-Schnitt-Methode" ein zweidimensionales Bild zeichnen lassen können, hängt
damit zusammen, dass die Jacobi-Matrix hier nur
von x abhängt. Was aber ist zu tun, wenn dies nicht so ist?
Im Wesentlichen gibt es drei Methoden. Es lohnt sich, diese zu untersuchen, denn im Kapitel Fraktale
werden wir noch häufig darauf zurückkommen. Am folgenden Bild
sind die ersten beiden Methoden ausführlich dargestellt:
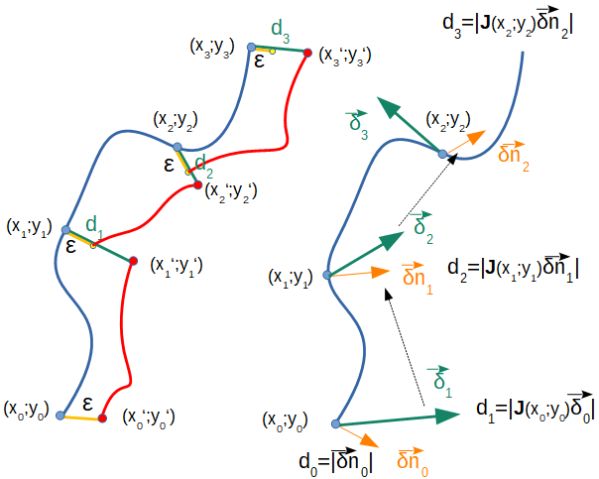
Zunächst zur linken Seite des Bildes. Hier kommt man völlig ohne Jacobi-Matrix aus. Man vergleicht den Verlauf
zweier Punkte, die den Abstand ε besitzen. Damit auf diese Weise wenigstens annäherungsweise der (größere)
Lyapunov-Exponent für die Stelle (x0;y0) errechnet werden kann, muss ε sehr klein
sein. (Meist kommt es nicht darauf an, welchen Punkt (x0';y0') man im vorgegebenen Abstand wählt.
Sollte aber eine Abhängigkeit
bestehen, dann bleibt immer noch die Möglichkeit, weitere Punkte im selben Abstand zu wählen und von allen
berechneten λ den Mittelwert zu berechnen.)
Wichtig hierbei ist, dass die iterierten Nachbarpunkte nach jeder Iteration wieder in den Abstand ε zum
Bildpunkt gebracht werden. Nun muss man nichts weiter tun, als alle dn /ε zu logarithmieren,
aufzusummieren und am Ende den Mittelwert zu bestimmen.
Rechts daneben ist die etwas aufwendigere Methode, die die Jakoci-Matrix verwendet, skizziert. Sie hat den
Vorteil, dass man hier die tatsächliche "Tangente", die in diesem Fall eine Ebene ist, verwenden kann. In einer
kleinen Umgebung des Punktes kann man daher statt der eigentlichen Abbildung die linieare Abbildung verwenden.
Man nehme daher einen Vektor (orange), bilde ihn mit Hilfe der Jakoci-Matrix ab und erhält als Bildvektor den
grün eingetragenen Vektor. Dessen Länge d1 wird bestimmt, logarithmiert und auf einen Speicher geschrieben.
Nun bringt man diesen Bildvektor auf die Länge des ursprünglichen Vektors (orange) und bilde ihn mit der
Jacobi-Matrix am Bildpunkt ab. Dies ergibt den grünen Vektor mit der Länge d2. Kommt beim letzten
Iterationschritt an, bestimmt man noch den Mittelwert aller log(di). Um einigermaßen verlässliche
Werte für λ zu bekommen, ist ein erheblicher Rechenaufwand notwendig. Daher nun zur dritten Methode,
die auch FLI (= Fast Lyapunov Indicator) genannt wird. Er eignet sich besonders gut, um
sogenanntes "schwaches Chaos" zu erkennen . Hat man das Matrix-Verfahren verstanden, muss man nur wissen, dass
keine Summe plus Mittelwert über alle log(di)gebildet wird. Man verwendet statt dessen das
Supremum aller log(di) und iteriert bis zu einem relativ kleinen Wert N.
Sie können für alle drei Methoden die passenden Sketche runterladen. Versuchen Sie selbst eine etwas andere
Farbzuordung zu wählen. Es ist immer wieder erstaunlich, wie sehr das Bild von dieser Zuordnung abhängt.
Das folgende Bild wurde mit der Supremum-Methode erstellt.

StandardMap-Lyapunov y-Schnitt .
StandardMap-Lyapunov x-Schnitt Fraktal .
StandardMap-Lyapunov x-Schnitt Fraktal Multi-Thread .
StandardMap-Lyapunov Epsilon-Methode .
StandardMap-Lyapunov Matrix-Methode .
StandardMap-Lyapunov Supremum-Methode .
Menu