Wege ins Chaos

Dynamische Systeme

Wege ins Chaos

Was sieht man im Bild links?

Eine relativ einfache Struktur im Zentrum. Es gibt größere gleichgefärbte Gebiete. Und darum herum ein Farbchaos. Jedes Pixel scheint eine andere Farbe als die Nachbarpixel zu haben. Etwas poetischer ausgedrückt könnte man sagen, wir sehen eine "Insel im Chaosmeer". Aber sehen Sie genau hin: Es scheint auch im Chaosmeer gewisse Strukturen zu geben...

Chaos ist uns auf diesen Seiten schon häufig begegnet. Im Kapitel Simulationen: Doppelpendel, Kicked Rotator, im Kapitel Maps: Standardmap und auch in diesem Kapitel: Feigenbaum-Diagramm. Der Lyapunov-Exponent gab uns sogar eine Möglichkeit, den Grad des Chaos zu messen.

Wir werden hier anhand der genannten Beispiele versuchen, uns einen Überblick zu verschaffen: Ist ein System stabil? Wie nah ist es an chaotischem Verhalten? Reicht eventuell eine winziger Impuls, so dass es sich jeder weiteren Berechenbarkeit entzieht?

Zu Beginn müssen einige häufig in diesem Zusammenhang benutzte Begriffe geklärt werden:

Konfigurationsraum: Beim Doppelpendel gibt es zwei Winkel, die den Ort des Pendelkörpers eindeutig beschreiben. Auch die Oberfläche eines Torus (T2) kann durch zwei Winkel beschrieben werden. Daher sagen wir, der Konfigurationsraum eines Doppelpendels ist die Oberfläche eines zweidimensionalen Torus. Und beim mathematischen Pendel? Es gibt genau einen Winkel, um die Lage dessen Pendelkörpers zu beschreiben. Daher ist der Konfigurationsraum dieses Pendels ein Kreis. Vielleicht wenden Sie nun berechtigterweise ein, dass man doch auch die Pendellängen und den Punkt der Aufhängung kennen muss, um genau zu wissen, wo sich der Körper im Raum aufhält. Aber darum geht es im Konfigurationsraum nicht. Es geht einzig und allein darum, wo sich der Körper bei dieser fest vorgegebenen Maschine befinden kann und wieviele Parameter man braucht, all die möglichen Orte zu beschreiben.

Phasenraum: Beim Mathematischen Pendel können Sie zuschauen, wie eine "Trajektorie" in den 2-dimensionalen Phasenraum gezeichnet wird. Als Ergebnis bekommt man ein so genanntes "Phasendiagramm", wie im Bild links. Die waagrechte Achse gibt den Winkel, die senkrechte die Winkelgeschwindigkeit des Pendelkörpers an. Im mittleren Bereich gibt es auch einige Kreissegmente. Die können hier entstehen, wenn man auf das Pendelbild klickt und damit den Pendelkörper schlagartig auf die Höhe des Mausklicks hebt. Im Phasenraum geht es also mehr, als nur um den Ort des Körpers. Um seinen Zustand zu beschreiben, reicht der Winkel nicht, man muss auch seine Winkelgeschwindigkeit dort kennen. Der Kicked Rotator liefert, nach dem Bild auf der Kicked Rotator-Seite links, ein ganz ähnliches Phasendiagramm. Auch das Bild rechts daneben zeigt ein Phasendiagramm, nur diesmal sehen wir nichts als chaotisch verteilte Punkte.
Wenn man aus dem Phasendiagramm des mathematischen Pendels einen Torus (Bild darunter) formt, indem die untere Seite zur oberen gebogen wird und danach der so entstandene Zylinder so verbogen wird, dass die beiden Öffnungen aufeinander liegen, dann befinden sich alle Trajektorien auf der Oberfläche dieses Torus.

Dort sind die Punkte der Trajektorien durch die Angabe zweier Winkel, einen für den blauen und einen für den roten Kreis, eindeutig bestimmt.
Wieviele Dimensionen hat denn eigentlich der Phasenraum des Doppelpendels? Zu zwei Winkeln kommen nun zwei Winkelgeschwindigkeiten hinzu, also vier Dimensionen. Zeichnen können wir das natürlich nicht mehr. Wenn wir aber, wie in allen anderen hier zu besprechenden Fällen auch, davon ausgehen, dass der Vorgang reibungsfrei abläuft, dann gilt der Energieerhaltungssatz. Damit gibt es eine Beziehung zwischen den vier Größen. Mit anderen Worten: Man braucht dann nur noch drei Dimensionen. Stellen wir auch noch die Schwerkraft ab, dann gilt auch der Impulserhaltungssatz und es bleiben noch zwei freie Paramter: Dann ist auch hier der

Phasenraum nur noch die Oberfläche des oben genannten T2-Torus.

Zum besseren Verständnis wurden bei der Animation eines Doppelpendels die aktuellen Winkel der beiden Pendel bei jedem neu berechneten Näherungswert im Diagramm eingetragen. Im wellenartige Bildes links wurden als x-Achse der Winkel des oberen und als y-Achse der Winkel des unteren Pendels eintragen. Dadurch entstehen unzählige Punkte, wenn man, wie zu diesem Bild, den Sketch lange laufen lässt. Es werden doch immer die gleichen Kurven wieder und wieder gezeichnet. Die Schwinung muss daher periodisch sein. Das obere Pendel könnte sich zum Beispiel drei mal und das untere Pendel in der gleichen Zeit zwei mal drehen. Die sogenannte "Rotationszahl" wäre dann 3:2. Formen Sie nun gedanklich aus dem Phasenbild links wieder einen T2-Torus. Dann erkenne Sie, dass in diesem Fall die Linien niemals die ganze Torus-Oberfläche ausfüllen werden. Verwendet man aber eine irrationale Ratationszahl, dann wird irgendwann ein sehr viel gräßerer Teil oder gar die gesamt Oberfläche bedeckt.
Wie auch immer: Alle Pendelbewegungen, die hier beobachtet werden können, sind quasiperiodisch und einige wenige sind periodisch. Das bedeutet, dass es hier kein Chaos gibt! Probieren Sie es aus! Im Sketch Doppelpendel ohne Schwerkraft können Sie ganz verschiedene Rotationszahlen ausprobieren.

Energiefläche (E = konstant): Die obigen Überlegungen zum Doppelpendel mit konstanter Energie reduzieren die Dimension des Raumes der real erreichbaren Punkte des Phasenraums. Dieser kleinere Raum wird Energiefläche genannt. Im Fall des Doppelpendels ist das ein T3-Torus, dessen Oberfläche dreidimensional ist. Weil man sich diesen Torus nicht vorstellen kann, hilft man sich mit einem Gedankenexperiment: Wenn man den T2-Torus senkrecht aufschneidet und verbiegt, entsteht ein Zylinder. Den kann man wieder aufschneiden und man bekommt ein Rechteck. (Allerdings ist zu beachten, dass zwei Punkte auf gegenüberliegenden Seiten, in Wirklichkeit nur einen Punkt darstellen.) Überträgt man diese Modellvorstellung auf den T3-Torus, dann bekommt man nach zweimaligem "aufschneiden" einen Quader. Die Energiefläche eines Doppelpendels, bei dem die Energie konstant bleibt, ist daher topologisch gesehen ein Quader. Wenn Sie das verstanden haben, dann können Sie sicher auch sagen, was die Energiefläche beim mathematischen Pendel (ohne Reibung) ist. Die Antwort finden Sie ganz unten...

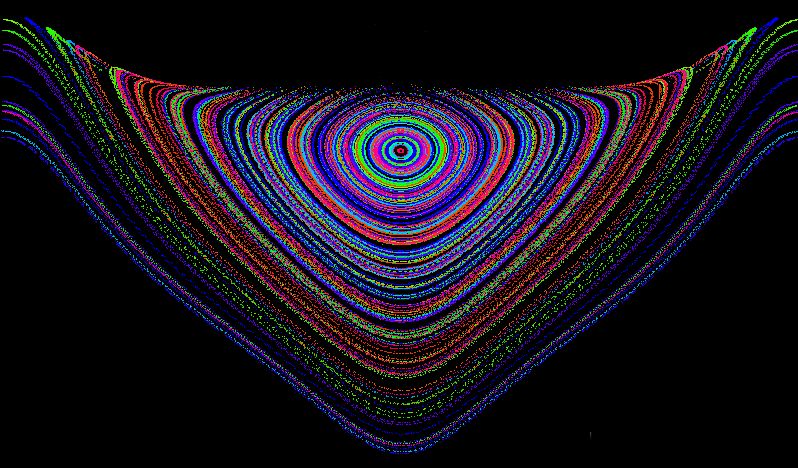
Invariante Menge: Beim Doppelpendel ohne Reibung und ohne Schwerkraft ist, wie weiter oben bereits erwähnt, die Anzahl der freien Parameter weiter reduziert. Die so eingeschränkte Energiefläche heißt "invariante Menge". Das obige Bild zeigt einen Poincaré-Schnitt eines 3-dim Phasendiagramms für den Spezialfall der Schwerelosigkeit. Die unteren Trajektorien kommen zustande, wenn sich das obere Pendel überschlägt. Jede dieser Trajektorien hat auf der Oberfläche eines T2-Torus Platz. Man sagt, die T3-Energiefläche wird durch invariante T2- Mengen "geblättert". Im folgenden Sketch weiter unten können Sie selbst ein derartiges Phasendiagramm im Browser erzeugen. Bei jedem Klick werden drei weitere Trajektorien eingetragen. Wenn Sie in die untere linke Ecke klicken, wird alles gelöscht und drei neue Trajektorien gezeichnet. Beachten Sie, dass die Linien nur deshalb teilweise gestrichelt erscheinen, weil nicht genügend Folgepunkte errechnet werden. Sehr viel schneller und mit tausenden von Start- und Folgepunkten geht es mit der threaded-Version (sofern Ihr Processor mehr als 2 Cores hat ;-)). Es lohnt sich, das Doppelpendel ohne Schwerkraft noch weiter zu untersuchen. Schauen Sie sich dazu das nächste nächste Kapitel an.

Poincaré-Schnitt: Wenn man allerdings ein Phasendiagramm für ein Doppelpendel im Schwerefeld der Erde oder für einen Kicked-Rotator zeichnen will, dann muss man sich mit dem Problem rumschlagen, dass in beiden Fällen drei Freiheitsgrade existieren. Weshalb dies beim Doppelpendel der Fall ist, habe wir schon besprochen. Beim Kicked Rotator gibt es zwar nur einen Pendelstab und es existiert auch kein Schwerefeld, dafür aber gilt der Energieerhaltungssatz wegen der periodischen Kraftstöße nicht. Und außerdem bleibt die Frequenz der Kraftstöße. Für solche Fälle bedient man sich der Hilfe eines Poincaré-Schnitts, wie er im Bild links angedeutet ist. Es werden nur die Durchstoßpunkte von einer Seite aus eingezeichnet. Im Falle des Kicked Rotators wählt man etwa immer genau den Moment, in dem der Kraftstoß erfolgt. Beim Doppelpendel kann man beispielsweise immer genau den Zustand wählen, bei dem das untere Pendel von links her schwingend durch die Ruhelage geht. Der Torus links soll eine periodische Bewegung des Doppelpendels darstellen. Dir Rotationszahl ist 1:4, d.h. während sich das obere Pendel einmal dreht, dreht sich das untere Pendel vier mal. Ein Poincaré-Schnitt würde lediglich einen Punkt zeigen, gleichgültig, wo der Schnitt erfolgt. Ist die Rotationszahl aber nicht rational, dann wird die Bewegung die gesamte Oberfläche des Torus ausfüllen. Der Poincaré-Schnitt wäre ein Kreis (bzw. eine andere geschlossene Linien, wie zum Beispiel eine Ellipse, wenn der Torus verformt ist.)

Die Poincaré-Schnitte für den Kicked Rotator als auch für das Doppelpendel werden im Kapitel Maps genauer untersucht. Es lohnt sich dort mal vorbeizuschauen...
Im Fall des Doppelpendels ohne Schwerkraft, gibt es ja nur zwei freie Parameter. Warum wir weiter oben dennoch einen Poincaré-Schnitt zeichnen ließen, statt einfach nur ein Phasendiagramm, wie im Fall des mathematischen Pendels, erfahren Sie im anschließenden Kapitel.

KAM-Theorem: Der Kicked Rotator und das Doppelpendel sind nur zwei Beispiele, bei denen man zum besseren Verständnis der Bewegung einen Poincaré-Schnitt erstellt. Selbst in Medizin oder Astronomie kann man mit diesen Phasendiagramm-Schnitten (=Surface of Section) zu wesentlichen Erkenntnissen kommen.

Das obige Bild ist ein Ausschnitt aus einem Poincaré-Schnitt des Doppelpendels bei einer bestimmten Gesamtenergie. Die durchgezogenen Linien repräsentieren sogenannte KAM-Tori , benannt nach drei Mathematikern Kolmogorow, Arnold und Moser. Sie umkreisen den Phasendiagramm Torus bzw. Zylinder. Es folgen Richtung Mitte ellipsenförmige Bereiche. Im Zentrum der Inseln müssen Sie sich einen Punkt denken. Hier schwingt das Doppelpendel periodisch und der Poincaré-Schnitt der zugehörigen Bewegung besteht lediglich aus diesem einen Punkt. Allen derartigen Punkten ist eine Rotationszahl zugeordnet. Angenommen, die Zahl wäre 3:4. Dann bedeutet das, dass, wenn sich das obere Pendel 3 mal gedreht hat, das untere Pendel exakt 4 Umdrehungen durchgeführt hat. Zwei solche Gebiete sind von Trajektorien umgeben, die dazwischen einen hyperbolischen Fixpunkt aufweisen. (In obigem Bild ist er irgendwo in den gelben Bereichen zu finden.)
Noch weiter Richtung Bildmitte folgen kleinere, von Chaos umgebene "Inseln". Diesen Bereich nennt man Cantorus oder Cantor-Menge , benannt nach dem Mathematiker Georg Cantor. Die Cantor-Menge ist fraktal. Das heißt unter anderem, dass man bei stärkerer Vergrößerung immer wieder ähnliche Strukturen findet. Wie Sie sehen, kann es zwischen den Inseln Bereiche von Chaos geben.

Was besagt nun das KAM-Theorem? Wir versuchen die Aussage an einem Beispiel nachzuvollziehen. (Wer es genauer wissen will, schaut im Internet nach der exakten Formulierung.)

Nachdem Newton das sogenannte "Zweikörperproblem" am Beispiel Sonne-Erde gelöst hatte, war die Hoffnung groß, dass man auch das "Dreikörperproblem" (Beispiel Sonne-Jupiter-Erde) würde lösen können. An Bemühungen hat es im 19. Jahrhundert nicht gefehlt. Vergeblich! Im letzten Jahrhundert setzte sich nach und nach die Überzeugung durch, dass das Problem nicht "integrabel", und damit nicht lösbar ist. Selbst numerische Näherungslösungen taugen nichts, denn wie soll man wissen, ob eine winzige, rechnerisch nicht fassbare Änderung am Anfang zu völlig verschiedenen Ergebnissen führt. Bleiben wir bei Sonne, Jupiter und Erde. Zunächst hatte man es mit einem 18-dimensionalen Lösungsraum zu tun. Wenn man aber Symmetrien nutzt, das Koordinatensystem geschickt wählt, vereinfachenderweise davon ausgeht, dass alle drei Körper sich nur in einer Ebene bewegen und dann noch der Erde eine Masse nahe Null gibt, ja dann hat man es nur noch mit eine dreidimensionalen Energiefläche zu tun. Diese Vereinfachung nennt man "ebenes, eingeschränktes Dreikörperproblem". Und integrabel ist das System dann auch noch.

Der Poincaré-Schnitt wird dann für die Bewegung der Erde einen KAM-Torus zeigen. Periodisch kann die Bewegung nicht sein, denn ein Jupiterjahr ist 11,862972 Erdenjahre. Das bedeutet, dass Jupiter der Erde ganz unregelmäßig "Schwung" gibt. Denken Sie an eine Kinderschaukel. Will man dort einen großen Ausschlag erreichen, muss man jedesmal an geeigneter Stelle Kraft anwenden. Also zum Beisiel bei jedem dritten Mal, wenn die Schaukel die aktuell maximale Auslenkung erreicht hat. Wendet man die Kraft irgendwann und schon garnicht regelmäßig an, dann wird das Kind auf der Schaukel zu Recht protestieren.

Was nützt uns aber dieser Spezialfall, wenn er in keinster Weise der Wirklichkeit entspricht. Hier kommt das KAM-Theorem zum Einsatz. Es garantiert im Falle einer quasiperiodischen Bewegung, nach Anwenden einer hinreichend kleinen Störung, Stabilität. Das heißt, nach Auftreten der Störung bleibt die Bewegung (unter bestimmten Voraussetzungen) quasiperiodisch. Die Störung dabei ist die Änderung der Masse der Erde auf die wahre Größe. Damit kommt man der realen Situation schon sehr nahe, denn die Bewegung der Planeten mit der Sonne findet nahezu in einer Ebene statt. Das KAM-Theorem beantwort damit gleichzeitig eine Frage, die die Wissenschaftler schon seit langer Zeit beschäftigt hat: Weshalb sind die Bahnen von Jupiter und Erde weitgehend stabil?

Um das gerade Gelernte noch zu vertiefen, kommen wir auf die Poincaré-Schnitte der HRV-Parameter (HRV = Herzratenvariabilität) zurück. Sie haben richtig gelesen: Es geht um ein wichtiges Thema der Medizin. Kann man, sofern man aus den beiden wesentlichen Parametern SD1 und SD2 des Herzschlags tatsächlich einen Poincaré-Schnitt erzeugen und die noch wichtigere Frage: Was würde ein solches Diagramm nutzen?

Die erste Frage kann man vorbehaltlos mit "ja" beantworten. Solche Diagramme werden tatsächlich gemacht. Die Frage nach dem Nutzen wird z. B. auf der Seite Allgemeinarzt-online ausführlich beantwortet. Was, werden Sie sich fragen, hat das Ganze mit dem KAM-Theorem zu tun? Erfreulicherweise ist dies sehr einfach zu bentworten: Wenn der Bereich mit den Punkten relativ groß ist, dann ist das Herz in einem Zustand, der der pseudoperiodischen Bewegung des Doppelpendels ähnlich ist. Das aber heißt, dass kleine Störungen den Zustand nicht wesentlich ändern. Denn, eines ist gewiss: Würde das Herz im chaotischen Bereich landen, würde Herzkammerflimmern eintreten. Damit überlebt man nur wenige Minuten. Ein großer Punkte-Bereich garantiert also, dass selbst bei einer Störung des Herzrhythmusses kein Herzkammerflimmern zu befürchten ist. Umgekehrt bekommt man die auf den ersten Blick merkwürdige Konsequenz, dass ein sehr regelmäßig schlagendes Herz, also eines, bei dem die Punkte dicht beieinander liegen, wesentlich gefährdeter ist, in Chaos abzugleiten. Denn das KAM-Theorem gilt nur für quasistationäre Bewegungen.

Sketch Animation Doppelpendel ohne Schwerkraft.

Sketch Doppelpendel ohne Schwerkraft Poincaré-Schnitt.

Sketch Doppelpendel ohne Schwerkraft threaded Poincaré-Schnitt.

Menu

Die Energiefläche eines mathematischen Pendels ist ein Rechteck.